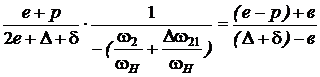Или, например, мотор-колесо электромобиля с исключенным из привода редуктором и системой управления вращения, бегущим магнитным полем двигателя.
Несколько другим является направление по созданию управляемых приводов с переменной структурой силовой схемы. Переменной может быль структура рычажной группы или передаточной. Отличительным свойством механизмов с переменной структурой является их способность переходить из одного вида механизма в другой, обеспечивая холостой и рабочий режимы без введения в кинематическую цепь дополнительных звеньев, удлинять или укорачивать ход рабочего звена, формируя холостое положение.
Переменная структура передач применяется в планетарных коробках-автоматах, где планетарные ряды формируются изменением тормозных регламентов.
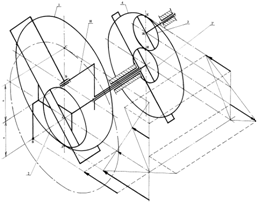
Автором предложена идея совмещения рычажного привода с дифференциальной схемой для получения механизмов с компактной конструкцией и управляемой кинематикой. В результате синтезированы и запатентованы четыре отвечающие этим условиям схемы замкнутого дифференциала [1, 2, 3, 4] (рис. 1) со свойством формировать точное прямолинейное движение без направляющей на кинематическом принципе.
|
а |
б |
|
в |
г |
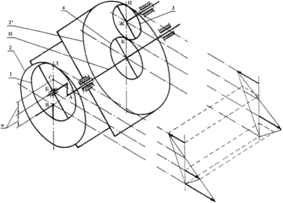
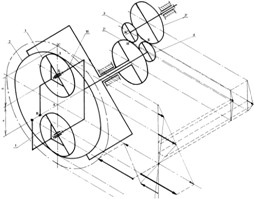
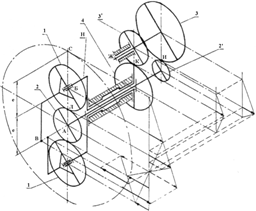
Рис. 1 Схемы дифференциалов с точным поступательным движением точки на сателлите:
а – схема 1; б – схема 2; в – схема 3; г – схема 4
Цель исследования
Основной целью выполненного исследования схем являлось получение зависимости движения рабочей точки на сателлите от внутренних отклонений геометрии и кинематики. Она позволяет анализировать перемещения рабочего органа при возможных ошибках изготовления и сборки. Уравнение также позволяет исследовать возможности управления траекторией, изменением кинематики замыкающей ступени при работе привода, например в ДВС, в рулевой системе или в шагающем транспортном средстве.
Содержание исследования
Кинематически траектория точки формируется сочетанием направлений и величин переносной и относительной скоростей в плоскопараллельном движении сателлита. Поэтому управлять траекторией можно, изменяя эти векторы. Например, можно управлять длиной хода ДВС, изменяя тем самым степень сжатия в цилиндре. Зазоры и отклонения от теоретических размеров звеньев также влияют на геометрию траектории.
К геометрическим влияющим факторам отнесены [5] – величина приращения радиусов D и число зубьев колес z. К кинематическим факторам отнесено изменение w2 , если это управляющая функция. К геометрическим факторам отнесено также смещение k с окружности радиуса е точки, формирующей прямолинейную траекторию, из-за ошибки разметки или ошибки в положении оси водила р. Влияние каких-либо других величин не рассматривается, так как они входят в перечисленные ошибки.
Известно, что при обегании сателлитом во внутреннем зацеплении неподвижного центрального колеса точки на сателлите описывают гипоциклоиду [5], уравнение которой имеет вид:
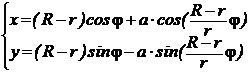 , (1)
, (1)
где: R – радиус центрального колеса;
r – радиус сателлита;
j – угол поворота сателлита;
а – радиус окружности расположения точки на сателлите, описывающей гипоциклоиду.
В зависимости от отношения радиусов R и r соприкасающихся
окружностей при их качении без проскальзывания кривая может быть циклически
замкнутой или бесконечной, незамкнутой. Циклическая гипоциклоида представляет
собой многогранную симметричную фигуру, в бесконечности повторений не
изменяющуюся. Таким образом, наибольшее прогнозируемое отклонение от прямолинейности
траектории по оси Y – это половина
максимального хода, т. е. ![]() .
.
При соотношении радиусов R = 2r и а=R / 2, заложенном в геометрии базового планетарного механизма и траектории мнимого центра скоростей сателлита в новых схемах дифференциалов, гипоциклоида вырождается в прямую:
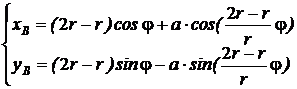 . (2)
. (2)
При подстановке а = lБВ = е получаем уравнение прямой:
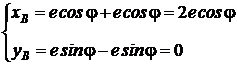 . (3)
. (3)
Условие сохранения прямолинейности должно обеспечивать выполнение следующих требований:
1. R / r = 2 при любых R2 = 2e + D и R1 = e + D.
2. D – неизменно при подборе z2 и z1.
3. U2Н – неизменно при подборе чисел зубьев колес замыкающей ступени дифференциала.
В отличие от планетарного механизма, имеющего действительные колеса с R2 = R и R1 = r, предложенные дифференциалы имеют мнимые образующие окружности, которые чувствительны к отклонениям задающих параметров. При изменении скорости точки Л в результате округления D, или отношения U2Н, или наличии зазоров в подшипниках радиусы образующих гипоциклоиду окружностей изменятся с R= 2е до R* и с r = е до r*. Таким образом, траектория движения точки В из прямой преобразуется в гипоциклоиду точки В, для которой существует интересующая нас координата уБ.
Рассмотрим возможные варианты причин неустойчивости траектории.
1. Не выдержан размер D в результате округления числа зубьев сателлита 1 и центрального колеса 2.
2. Не выдержана величина U2Н в результате округления до целого чисел зубьев колес замыкающей ступени дифференциала.
3. Совокупное смещение точки Б из-за допусков изготовления и зазоров в подшипниках опор водила и сателлита.
4. Все предыдущие пункты в совокупности при наихудшем их сочетании.
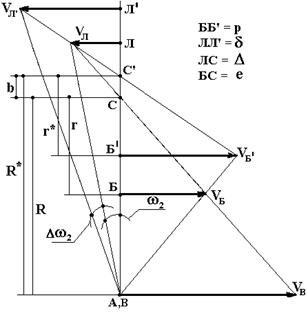
Выведем условия отклонения величины образующих радиусов в при разных условиях коррекции расчетных данных (рис. 2, 3, 4, 5).
|
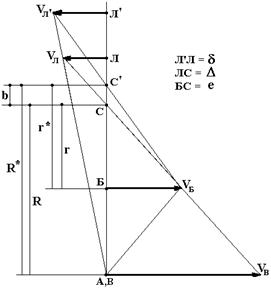
Рис. 2. Расчетный случай 1 |
Расчетный случай 1 – изменение D на величину δ (рис. 3.3): VБ = wH×e – const. Точка Л лежит на продолжении прямой АБ: АБ = БВ = еU2Н = w2/wН = const
Тогда
вектор
|
и ![]() ,
,
![]()
![]()
![]() ,
,
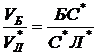 ,
,
![]()
![]() ,
,
где: ![]() – приращение радиусов R и
r.
– приращение радиусов R и
r.
Так как wН – положительная, а w2 – отрицательная, то:
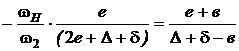 .
.
В соответствии с главным условием синтезированной схемы дифференциалов:
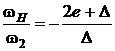 .
.
При подстановке получаем:
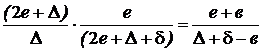 .
.
Окончательно общее приращение радиусов:
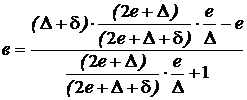 . (4)
. (4)
Проверим выражение по условию d = 0:
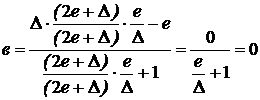 – условие верное.
– условие верное.
Радиусы смещенных образующих окружностей:
R* = R + в = 2е + Δ + в;
r* = r + в = е + Δ + в.
|
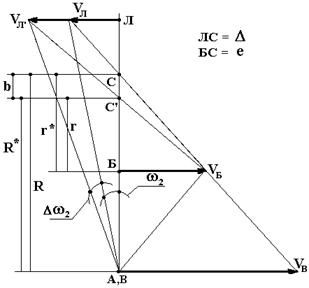
Рис. 3. Расчетный случай 2 |
Расчетный случай 2 – изменение U2Н на величинуDU и wH на величину = DwH (рис. 3.4): VБ = wH×e - const Точка Л лежит на продолжении прямой АБ: АБ = БВ = еR1, R2 – const
Тогда
вектор
|
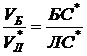 ,
,
![]() ,
,
![]() ,
,
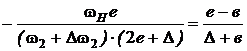 .
.
После преобразования получаем приращение радиусов:
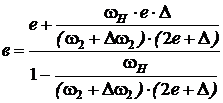 . (5)
. (5)
При Dw2 = 0:
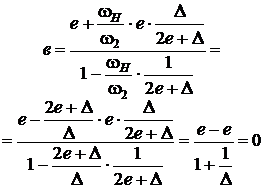 .
.
Радиусы смещенных окружностей:
R* = 2е + Δ – в;
r* = е + Δ – в.
|
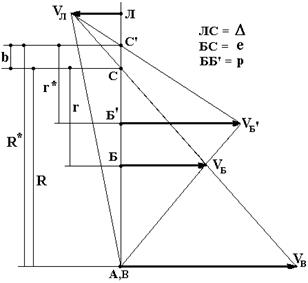
Рис. 4. Расчетный случай 3 |
Расчетный случай 3 – влияние зазоров в опорах и отклонений при изготовлении на положение т. Б. Обозначим приращение расстояния АБ через р. Точка Л лежит на продолжении прямой АБ АБ’ = е + р, U2Н = const
|
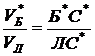 ,
,
![]() ,
,
![]()
![]() ,
,
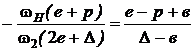 .
.
При
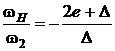
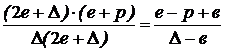 ,
,
![]() ,
,
![]() ,
,
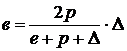 . (6)
. (6)
Величина измененных радиусов:
R* = R + в = 2е + Δ + в;
r* = r – р + в = е + Δ – р + в
|
Рис. 5. Расчетный случай 4 |
Расчетный случай 4 – все виды смещений (рис. 3.6):
|
Используя условие:
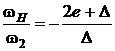 ,
,
окончательно получаем:
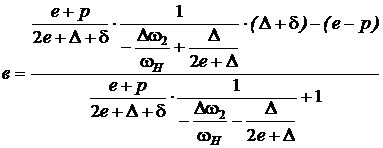 . (7)
. (7)
При d = 0; Dw2 = 0; р = 0:
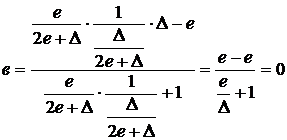 – верно.
– верно.
Измененные радиусы образующих окружностей соответственно:
R* = R + в = 2е +Δ + в;
r* = r – р + в = е + Δ – р + в.
Для всех случаев ошибок траектория отклонения точки В от прямой описывается как:
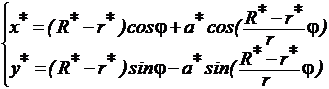 ,
,
или:
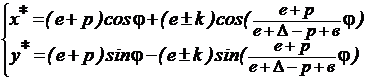 . (8)
. (8)
Ошибка k для прямой траектории входит в величину а, поэтому она не изменяет кинематику. При обнулении всех ошибок, кроме k, получаем уравнение эллипса (рис. 11):
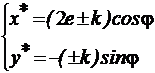 .
(9)
.
(9)
Уравнение (9) показывает, что малая ось эллипса равна 2k, так как при обратном ходе получаем (–sin φ). А ход может быть короче или длиннее.
Заключение
Уравнения (8 и 9) применяются для прогнозирования траектории без изменения первоначальной схемы привода. Например, для получения величины поднятия ноги шагающего транспортера надо ввести уменьшение расстояния а на величину k = h / 2, где h – высота неровностей дороги [5].
При управлении параметром а траектория становится короче или длиннее, что можно применить при управлении степенью сжатия в ДВС [6, 7].
Отклонение размера а из-за допусков изготовления и сборки в уравнениях гипоциклоиды также может нарушить прямолинейность траектории. При величине отклонения в пределах допуска на изготовление, полученная таким образом координата k может быть компенсирована зазором в шарнирах Б и В. При большой величине отклонения от прямолинейности требуется специальный компенсатор бокового хода для шарнира В (см. рис. 1).
Рецензенты:Ляшенко М.А., д.т.н., профессор, зав. кафедрой «Автомобиле- и тракторостроение», Волгоградский государственный технический университет, г. Волгоград;
Матлин М.М., д.т.н., профессор, зав. кафедрой «Детали машин и ПТУ», Волгоградский государственный технический университет, г. Волгоград.
Библиографическая ссылка
Зайкин О.А., Шеховцов В.В., Годжаев З.А. ИССЛЕДОВАНИЕ УСЛОВИЙ НАРУШЕНИЯ РАБОЧЕЙ ТРАЕКТОРИИ ДЛЯ УПРАВЛЕНИЯ РАБОЧИМ ПРОЦЕССОМ АВТОМОБИЛЬНЫХ АГРЕГАТОВ // Современные проблемы науки и образования. 2015. № 1-2. ;URL: https://science-education.ru/ru/article/view?id=19946 (дата обращения: 26.02.2026).




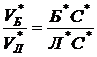 ,
,
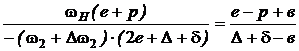 ,
,