Постановка задачи
В работе рассматривается задача формирования устойчивой многосвязной системы, содержащей в своем составе неустойчивые объекты, за счет введения стабилизирующих неголономных связей между подсистемами. Многообразие постановок задачи определяется тем, что подсистемы, входящие в состав МСАУ, могут быть:
1) статически неустойчивыми;
2) динамически неустойчивыми.
Кроме того, одни подсистемы могут быть статически неустойчивыми, другие – динамически неустойчивыми, а третьи – устойчивыми.
Целью работы является выявление особенностей многосвязного управления статически неустойчивыми подсистемами и построение процедуры формирования связей между ними из условия обеспечения устойчивости многосвязной системы в целом. Решается задача формирования необходимого и достаточного условия устойчивости многосвязной системы, состоящей из статически неустойчивых подсистем.
При осуществлении управления неустойчивыми объектами необходимо учитывать их физическую природу, особенности их строения и функционирования.
Для проверки алгоритмов управления нелинейными механическими объектами часто в качестве примера используются маятники: однозвенный и многозвенный, классический и перевернутый, автономный и группа маятников. Во множестве публикаций предлагаются различные способы управления по обратной связи и с дополнительными устройствами, которые переводят неустойчивый маятник в устойчивое положение равновесия.
Описание подхода к исследованию МСАУ
При исследовании МСАУ [1] чаще всего используют запись уравнений движения системы в векторно-матричной форме относительно ее физических координат. МСАУ, в которой все связи между подсистемами осуществляются через многомерный объект, описываются следующими уравнениями движения:
![]() (1)
(1)
где
![]() ,
, ![]() ,
, ![]() ,
, ![]() –
векторы задающих, регулируемых, управляющих и возмущающих воздействий
соответственно;
–
векторы задающих, регулируемых, управляющих и возмущающих воздействий
соответственно; ![]() – матричная передаточная
функция (МПФ) многомерного объекта по управляющим воздействиям,
– матричная передаточная
функция (МПФ) многомерного объекта по управляющим воздействиям,
![]() diag
diag![]() – МПФ сепаратных регуляторов.
– МПФ сепаратных регуляторов.
В качестве индивидуальной характеристики (ИХ) отдельной подсистемы рассматривается ее передаточная функция Фi(s) в режиме управления, когда подсистема функционирует в изолированном от других подсистем состоянии. Для МСАУ, соответствующей системе уравнений (1), передаточные функции индивидуальных характеристик подсистем имеют вид:
![]() .
.
Если все сепаратные подсистемы идентичны, т. е. для
всех ![]() ,
, ![]() , то
МСАУ называется гомогенной.
, то
МСАУ называется гомогенной.
Характеристикой связи (ХС) между k подсистемами в полной МСАУ, состоящей из n подсистем и имеющей математическую модель (1), является значение
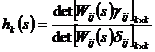 ,
, ![]() ,
,
где Wij(s) – передаточные функции элементов матрицы многосвязного объекта управления,
![]()
![]()
![]() .
.
Характеристическое уравнение гомогенной МСАУ имеет вид:
![]() . (2)
. (2)
Рассмотрим уравнение
![]() (3)
(3)
относительно переменной x, которое получается из (2) подстановкой Φ(s)=x. Уравнение (3) называется алгебраическим уравнением связи. Справедлив следующий критерий устойчивости [1].
Критерий устойчивости. Для устойчивости линейных гомогенных МСАУ необходимо и достаточно, чтобы годограф амплитудно-фазовой характеристики (АФХ) Ф(jw) для всех wÎ(–¥,+¥), построенный на плоскости корней уравнения связи (3), не охватывал ни один из его корней.
На основе критерия устойчивости сформулированы критерии устойчивости гомогенных МСАУ, содержащих нелинейные элементы в составе подсистем, а также разработаны методики синтеза регуляторов сложных систем[4].
Классификация МСАУ, содержащих неустойчивые объекты
Управление группой неустойчивых объектов возможно как в режиме автономной работы каждого элемента и как единой системы, эти способы имеют и достоинства, и недостатки. Проблема стабилизации неустойчивого положения равновесия управляемой системы сопряжена с определенными трудностями, особенно если ресурсы органов управления ограничены.
В зависимости от этого можно выделить четыре группы МСАУ, существенно различающиеся по организации и введению стабилизирующих связей между подсистемами.
1. Задана группа неустойчивых объектов, работающих автономно. Требуется установить, можно ли между ними организовать перекрестные связи, чтобы получить управляемую устойчивую многосвязную систему. Примером таких объектов может выступать группа перевернутых маятников.
2. Неустойчивые объекты объединены в систему, т. е. между ними существуют перекрестные связи, но можно организовать дополнительные перекрестные связи, стабилизирующие работу системы в целом.
Примером такой системы является многозвенный перевернутый маятник, прототипом служит гимнаст на перекладине. Многозвенный перевернутый маятник представляет собой систему, состоящую из статически неустойчивых, связанных подсистем. В случае, когда все звенья маятника одинаковы, МСАУ является гомогенной. Если же звенья имеют различные физические свойства (длину, толщину, материал, из которого они изготовлены, и т. д.), то МСАУ гетерогенная.
Двойной перевернутый маятник представляет собой вполне управляемую систему [4], поэтому система из нескольких многозвенных маятников также является управляемой. Для получения устойчивой МСАУ к уже имеющимся естественным связям добавляются дополнительные стабилизирующие перекрестные связи между звеньями.
3. Система формируется из неустойчивых автономных объектов. Их физическая сущность такова, что объединение в систему по принципу п. 1 невозможно. Изменения параметров и состояний объектов происходят независимо друг от друга. В этом случае устойчивость системы может быть достигнута за счет введения многосвязного регулятора между подсистемами, объединении объектов в единую систему и компенсации неустойчивости за счет свойств регулятора.
Примером таких объектов может выступать группа перевернутых маятников, установленных на тележках. После введения связного регулятора маятники выступают в роли подсистем в составе единой системы.
4. Неустойчивые объекты входят в состав МСАУ, структура которой определена и не может быть изменена желаемым образом. В этом случае стабилизация МСАУ должна проводиться за счет введения многосвязного регулятора, определение параметров которого является основной задачей управления. При этом необходимо учитывать существующие связи между подсистемами, которые оказывают влияние на устойчивость системы. Усложняется характеристическое уравнение системы, а значит, изменятся алгоритмы анализа и синтеза МСАУ.
Примером такой системы могут служить сложные технические объекты, которые на некоторых режимах становятся неустойчивыми. В связи с тем, что изменение структуры таких объектов невозможно, необходимо изменять структуру регуляторов.
Во всех четырех случаях ставится задача определения параметров и структуры вводимых стабилизирующих связей для устойчивого функционирования системы в целом. Но в первом, втором и третьем случаях связи между подсистемами будут однократными (в первом и втором случаях – между объектами, в третьем – в многосвязном регуляторе), а в четвертом случае связи двукратные, что усложняет задачу регулирования.
Критерий устойчивости
Проанализируем решение задачи формирования устойчивой
МСАУ из неустойчивых подсистем за счет введения искусственных перекрестных
связей, а не за счет изменения структуры самих подсистем. Рассмотрим
формирование устойчивой двусвязной системы, состоящей из двух неустойчивых
подсистем с одинаковой индивидуальной передаточной функцией, которая равна ![]() ,
, ![]() .
.
Из практики известно, что при подаче сигнала в систему с обратной положительной связью необходимо введение инвертора для сохранения физического смысла управляющего сигнала. Искомую характеристику двумерной связи обозначим через H(s). В данном случае характеристика связи равна
![]() . (4)
. (4)
Далее для простоты будем считать, что связи в прямых
каналах равны 1: ![]() . Тогда характеристика связи H(s) будет представлять собой некоторый
полином от s.
. Тогда характеристика связи H(s) будет представлять собой некоторый
полином от s.
Характеристическое уравнение для двусвязной системы имеет вид:
![]() . (5)
. (5)
Запишем характеристическое уравнение в виде многочлена от переменной s. Используя критерий устойчивости Гурвица, определим структуру H(s) таким образом, чтобы полученная система была устойчива. Рассмотрим задачу синтеза связей между статически неустойчивыми подсистемами с использованием вышеописанного способа.
Пример 1.
Необходимо обеспечить совместное устойчивое функционирование двух статически
неустойчивых объектов первого порядка при помощи введения стабилизирующей связи
H(s) между ними. Передаточные функции
разомкнутых подсистем имеют вид ![]() . Так как объекты
охвачены единичной обратной положительной связью, то передаточные функции
замкнутых подсистем имеют вид
. Так как объекты
охвачены единичной обратной положительной связью, то передаточные функции
замкнутых подсистем имеют вид ![]() , где
, где ![]() . Запишем характеристическое уравнение
системы после введения двумерной связи с характеристикой H(s)
. Запишем характеристическое уравнение
системы после введения двумерной связи с характеристикой H(s)
![]() , (6)
, (6)
где H(s) – неизвестная функция.
Известно, что для устойчивости системы второго порядка необходимо и достаточно выполнение условия положительности всех коэффициентов. Коэффициент при s первого порядка отрицательный. Отсюда следует, что для компенсации неустойчивости объектов достаточно введение двумерной связи первого порядка. Пусть характеристика связи (4) имеет вид:
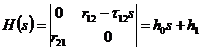 ,
,
где
![]() ,
, ![]() .
.
Тогда характеристическое уравнение системы (5), (6) примет вид:
![]() . (7)
. (7)
Из уравнения (7) можно получить:
– условие динамической устойчивости: h0 >2T; (8)
– условие статической устойчивости: 1+h1 >0. (9)
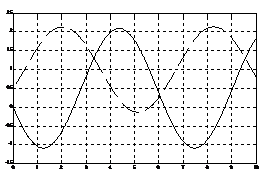
При 1+h1 >0, h0 =2T система находится на границе колебательной устойчивости (рис. 1, а).
|
|
|
|
Рис. 1. Переходные процессы в синтезированной системе:
а – h0=2T, r12r21=0.5, МСАУ на границе колебательной устойчивости;
б – h0=4T, r12r21=0,5, система устойчива
При 1+h1 =0,
т.е. ![]() система находится на границе
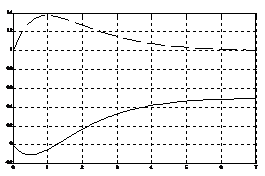
апериодической устойчивости. При выполнении условий (8), (9) система устойчива
и управляема (рис. 1, б)
с точностью до ε=0 (при действии на вход ступенчатых сигналов,
система находится на границе
апериодической устойчивости. При выполнении условий (8), (9) система устойчива
и управляема (рис. 1, б)
с точностью до ε=0 (при действии на вход ступенчатых сигналов, ![]() и
и
![]() на
первую и вторую подсистемы соответственно).
на
первую и вторую подсистемы соответственно).
Далее рассмотрим взаимное расположение годографа
амплитудно-фазовой характеристики (АФХ) сепаратной подсистемы F(jw) и корневых годографов xi(jw), i=1, 2 характеристического уравнения
связи ![]() при изменении частоты w от 0 до +∞ (рис. 2).
при изменении частоты w от 0 до +∞ (рис. 2).
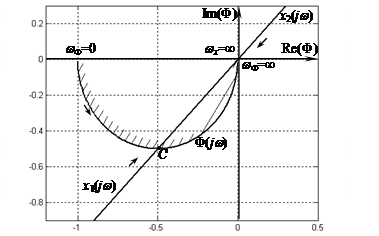
Рис. 2. Взаимное расположение годографов
Пересечением годографов F(jw) и xi(jw), i=1, 2 является точка С. В этой точке для сепаратных подсистем и связей наблюдается баланс амплитуд:
![]() , i=1, 2
, i=1, 2
и баланс фаз
![]() , i=1, 2.
, i=1, 2.
Обозначим частоту прохождения через точку С корневого годографа xi(jw), i=1, 2 через ωx, а частоту годографа АФХ F(jw) сепаратной подсистемы — через ωΦ. В зависимости от значений коэффициентов связей h1 и h0 пересечение годографов F(jw) и xi(jw), i=1, 2 происходит при разных значениях частот ωx и ωΦ. При h0=2T годографы одновременно проходят через точку пересечения C. При этом МСАУ находится на границе колебательной устойчивости, что согласуется со сделанными ранее расчетами и результатами моделирования.
Критерий устойчивости. Для устойчивости МСАУ, состоящей из статически неустойчивых подсистем первого порядка, необходимо и достаточно, чтобы частота корневого годографа ωx и частота ωΦ АФХ неустойчивой подсистемы в точке пересечения С удовлетворяли следующему неравенству: ωx < ωΦ.
Связь ![]() не является
физически реализуемой. На практике реализацию этой связи можно решить двумя
способами:
не является
физически реализуемой. На практике реализацию этой связи можно решить двумя
способами:
1) заменой идеального дифференцирующего звена на
реальное дифференцирующее, тогда характеристика связи ![]() ,
где τ<<1;
,
где τ<<1;
2) использованием сигнала управления по ошибке. Для этого гибкая связь h0s переносится за объект управления (интегратор), что эквивалентно сложению выходной координаты с несобственной ошибкой.
Применение вышеописанного способа определения стабилизирующей связи позволяет найти граничное значение характеристики связей.
Пример 2.
Рассмотрим многосвязную гомогенную систему, состоящую из четырех статически
неустойчивых подсистем с передаточными функциями ![]() .
Введем между подсистемами кольцевую неголономную связь H(s). Запишем характеристическое уравнение полученной МСАУ.
.
Введем между подсистемами кольцевую неголономную связь H(s). Запишем характеристическое уравнение полученной МСАУ.
![]() .
.
![]() .
.
Коэффициенты при степенях s3 и s отрицательные. Исходя из
этого зададимся желаемой характеристикой связи ![]() .
Тогда характеристическое уравнение имеет вид:
.
Тогда характеристическое уравнение имеет вид:
![]() .
.
Необходимые условия устойчивости системы:
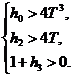 (10)
(10)
По критерию Гурвица МСАУ будет устойчива при выполнении условия:
![]() . (11)
. (11)
Рассмотрим частный случай, когда h3=1, T=1, тогда неравенство (11) примет
вид ![]() . Квадратичная форма в левой части распадается
на пару пересекающихся прямых
. Квадратичная форма в левой части распадается
на пару пересекающихся прямых ![]() и
и ![]() . Область G, удовлетворяющая условиям (10), (11),
является областью значений коэффициентов h0, h2,
при которых МСАУ устойчива (рис. 3).
. Область G, удовлетворяющая условиям (10), (11),
является областью значений коэффициентов h0, h2,
при которых МСАУ устойчива (рис. 3).
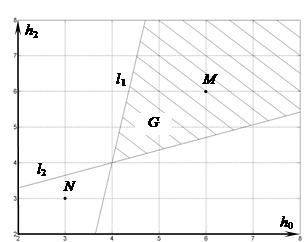
Рис. 3. Область расположения коэффициентов характеристики связи устойчивой МСАУ
Прямые l1 и l2 являются граничными значениями коэффициентов h0 и h2 характеристики связи H(s).
На рисунке 4 показано взаимное расположение
корневых годографов xi(jw), ![]() и годографа
подсистемы F(jw) при T=1 в двух случаях:
и годографа
подсистемы F(jw) при T=1 в двух случаях:
1) h0=6, h2=6
(соответствует точке M
на рисунке 4, которая находится внутри области устойчивости G), корневые годографы xMi(jω),
![]() построены
тонкой линией, начинаются в точках 1;
построены
тонкой линией, начинаются в точках 1;
2) h0=3, h2=3
(соответствует точке N
на рисунке 4 вне области G),
корневые годографы xNi(jω),
![]() изображены утолщенной линией, начинаются
в точках 2.
изображены утолщенной линией, начинаются
в точках 2.
При значениях коэффициентов характеристики связи, соответствующих точке M, МСАУ устойчива, что подтверждается результатами моделирования.
Для коэффициентов характеристики связи, соответствующих точке N, значения частот в точке пересечения B не удовлетворяют условию критерия устойчивости, поэтому МСАУ неустойчива.
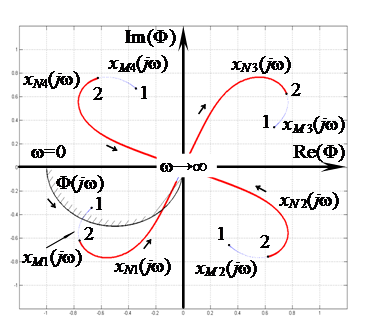
Рис. 4. Взаимное расположение корневых годографов и АФХ подсистемы
Методика определения характеристики компенсирующих связей заключается в выполнении следующего алгоритма.
1. Рассмотрим характеристическое уравнение МСАУ, состоящей из заданных статически неустойчивых подсистем с характеристикой связи H(s):
![]() .
.
2. Сформируем желаемое характеристическое
уравнение устойчивой МСАУ, например состоящей из устойчивых подсистем с
передаточной функцией ![]() и желаемой характеристикой
голономной связи h4.
и желаемой характеристикой
голономной связи h4.
![]() .
.
3. Искомая характеристика связи H(s) определится из равенства нулю разности этих уравнений:
![]() .
.
Отсюда: ![]() .
.
Выводы
Таким образом, характеристика связи зависит от выбора желаемого характеристического уравнения связи, которое задается из условия устойчивости. При этом невозможно указать граничные значения коэффициентов характеристики связи, т.е. синтезированная система является заведомо устойчивой с заданными запасами устойчивости.
Синтезированная характеристика связи может быть получена при различных структурах перекрестных связей. От распределения связей вид характеристического уравнения не изменится, т.е. МСАУ останется устойчивой, однако это влияет на качество переходных процессов. Качественные характеристики МСАУ могут определяться на этапе выбора желаемой передаточной функции и на этапе распределения характеристики связей между перекрестными связями. Поэтому в дальнейшем для качественного функционирования системы необходимо решить следующие задачи: определения структуры желаемого характеристического уравнения системы; оптимизации связей между подсистемами.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (14-08-97056 р_поволжье_а, 14-08-01019 А, 15-08-01146 А).
Рецензенты:Мунасыпов Р.А., д.т.н., профессор, заведующий каф. «Мехатронные станочные системы» Уфимского государственного авиационного технического университета, г. Уфа;
Васильев В.И., д.т.н., профессор, заведующий каф. «Вычислительная техника и защита информации» Уфимского государственного авиационного технического университета, г. Уфа.
Библиографическая ссылка
Ильясов Б.Г., Саитова Г.А., Халикова Е.А. УПРАВЛЕНИЕ НЕУСТОЙЧИВЫМИ ОБЪЕКТАМИ В СОСТАВЕ МНОГОСВЯЗНОЙ АВТОМАТИЧЕСКОЙ СИСТЕМЫ // Современные проблемы науки и образования. 2015. № 1-2. ;URL: https://science-education.ru/ru/article/view?id=19941 (дата обращения: 22.01.2026).