Бросковая подготовка как часть технической подготовки в баскетболе [5] направлена на обучение и совершенствование бросков с целью повышения их точности. Броски в баскетболе подразделяются на броски без отражения и с отражением мяча от щита [4]. Для обучения спортсменов технике баскетбольных бросков необходимо создать методы прицеливания и пространственного ориентирования для бросков двух разновидностей. Броски прямо в кольцо достаточно изучены и экспериментально проверены [3, 6, 8]. Броски с отражением мяча от щита сложно-ориентированы в пространстве и требуют научно-обоснованных положений о способах прицеливания для создания рациональных параметров полета мяча при различных координатах расположения бросающего на площадке [7]. Для создания метода прицеливания и пространственного ориентирования баскетбольных бросков с отражением мяча от щита необходимо провести исследования для проектирования инструментария по качественному определению координат отскока мяча от щита данных бросков. В настоящем сообщении представлены результаты теоретической и экспериментальной проверки возможности использования датчиков акустических волн для точного установления координат взаимодействия мяча с лицевой плоскостью щита при баскетбольных бросках.
Варианты определения координат
За основу работы устройства положена идея акустической локации. Суть этой идеи заключается в гипотезе о том, что при ударе мяча о щит возникает изгибная акустическая волна, фронт которой представляет собой расходящиеся концентрические окружности, скорость движения которых не зависит от расстояния от центра.
Рассмотрим способы получения координат точки удара мяча о щит, а также их достоинства и недостатки.
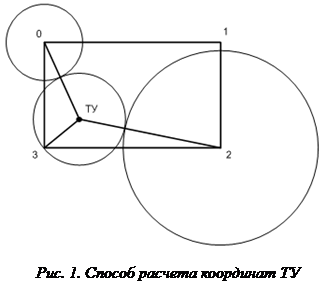
Один из способов расчета координат точки удара (ТУ) поясняет рисунок 1.
Точки 0, 1, 2 и 3 являются местами расположения пьезоэлектрических датчиков [1]. При указанном на рисунке расположении точки удара волна сначала придет в точку 3, затем в точку 0, и потом в точку 2. Таким образом, первым придет сигнал с третьего датчика (который станет стартовым), вторым придет сигнал с нулевого датчика, и третьим придет сигнал со второго датчика. Проведем две окружности:
1 - из точки 0 – радиусом, равным произведению скорости движения волны на величину задержки сигнала нулевого датчика относительно третьего датчика;
2 - из точки 2 – радиусом, равным произведению скорости движения волны на величину задержки сигнала второго датчика относительно сигнала нулевого датчика.
Далее необходимо провести окружность через точку 3 так, чтобы она касалась первых двух окружностей, как показано на рисунке 1. Центром проведённой окружности будет являться точка удара мяча о щит. Таким образом, точка удара определена с помощью трех датчиков (3, 0, 2). В случаи отскока мяча ближе к датчикам 1 и 2, для измерения координат отражения будут задействованы другие три датчика (например, 2, 1, 3).
Система измерения координат содержит четыре датчика ускорения, закрепленных в углах щита, сигналы от которых через усилители передается на аналого-цифровые преобразователи (АЦП) и далее в микроконтроллер [2]. Измерение запускается при превышении сигнала порогового уровня от любого АЦП, а далее отслеживаются отсчеты сигналов и анализируются переходы через максимальное значение по всем датчикам (включая опорный). При последовательном опросе датчиков под временем одного преобразования понимается время преобразования АЦП, умноженное на число датчиков. Если это время получается большим, то необходимо делать аппроксимацию полученных выборок и находить точку максимума аппроксимирующей функции, что позволит повысить точность.
В данном способе радиус окружностей будет определяться формулой:
![]() , (1)
, (1)
где i – номер датчика, U – скорость распространения круговой изгибной волны в щите, ![]() – время хода сигнала до i-го датчика, n – номер выборки с максимальным значением,
– время хода сигнала до i-го датчика, n – номер выборки с максимальным значением, ![]() – время одного преобразования.
– время одного преобразования.
Основным недостатком описанного способа является строгая привязка к скорости распространения волны, которая зависит от материала щита. Данное обстоятельство решается введением калибровки (в том числе и автокалибровки).
Экспериментальные исследования
Эксперимент проводился на специально разработанном модуле. Акустические датчики крепились к щиту с помощью прижимных винтов в центре креплений. Крепления привинчены к раме щита, что обеспечивает высокую надежность соединения. Равномерное распределение давления на датчик обеспечивает металлический прижимной диск. Для обеспечения электрической изоляции и поглощения акустических волн между датчиком и диском находится прокладка из вакуумной резины. Для обеспечения хорошего акустического контакта поверхность датчика и место крепления на щите были обработаны спиртом и смазаны глицерином. Центры датчиков располагались на расстоянии 15 см от границ щита. Сигналы с датчиков передавались в измерительное устройство через коаксиальные кабели типа «микротракт». Результаты измерений передавались в компьютер через интерфейс RS-232 с помощью кабеля PC-COM. Для отображения информации была разработана специальная программа «BallLocator».
После проведения серии баскетбольных бросков с работающей системой измерений было обнаружено, что результаты определения координат сильно зависели от точки удара, и никакие калибровки не позволяли получить правильное соответствие реальных и измеренных координат. При исследовании осциллограмм с датчиков было обнаружено следующее:
· сигналы датчиков имеют сложную форму с множеством выбросов разного знака, причем первый из этих выбросов как правило не имеет максимальную амплитуду;
· при изменении расстояния точки удара от датчика форма сигнала существенно изменяется вплоть до инверсии знака первого выброса;
· форма сигнала зависит от силы удара;
· кроме акустических сигналов, соответствующих изгибным волнам, датчики улавливают сигналы, проходящие через элементы металлической рамы, на которой крепится щит, причем скорость распространения звука по этим элементам много больше скорости изгибной волны в щите.
Все эти факторы приводят к тому, что время распространения сигнала не удается привязать ни к уровню, ни к характерным точкам осциллограмм сигналов.
Для выяснения причин получения недостоверных результатов и поиска оптимальных методик обработки сигналов от датчиков, было решено провести компьютерное моделирование процессов распространения изгибных волн в щите.
Компьютерное моделирование процессов, происходящих в щите
Оценка времени удара баскетбольного мяча о щит
Введем следующие обозначения: радиус мяча равен R, масса мяча равна M, избыточное давление воздуха внутри мяча равно P, скорость движения мяча равна V, время контакта мяча со щитом при ударе и отскоке равно T.
Примем следующие допущения:
1. 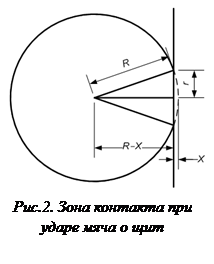 При ударе мяча о щит размеры и форма мяча остаются прежними (за исключением зоны контакта со щитом, которая имеет форму круга радиуса r (как показано на рисунке 2).
При ударе мяча о щит размеры и форма мяча остаются прежними (за исключением зоны контакта со щитом, которая имеет форму круга радиуса r (как показано на рисунке 2).
2. Давление P внутри мяча при ударе является постоянным.
3. Величина прогиба оболочки мяча X много меньше радиуса мяча R.
4. Масса части оболочки мяча, находящейся в контакте со щитом в момент удара, много меньше общей массы мяча M, поэтому изменением движущейся массы во времени можно пренебречь.
5. Мяч движется по нормали к поверхности щита.
6. Величина прогиба щита при ударе пренебрежимо мала по сравнению с величиной прогиба оболочки мяча X, поэтому можно считать, что мяч ударяется о жесткую недеформируемую стенку.
7. В каждой точке зоны контакта мяча со щитом величина давления мяча на щит равна величине избыточного давления в мяче P.
При этих допущениях сила взаимодействия мяча со щитом F = P?π?r2 = P?π?(R2-(R-X)2) = P?π?X?(2?R-X) ≈ P?π?X?2?R. Мы получили формулу для идеальной пружины с величиной коэффициента жесткости K = 2?π?R?P. Частота колебаний f для такой пружины с коэффициентом жесткости K и колеблющейся массой M равна ![]() . Тогда время контакта T равно половине периода собственных колебаний этой пружины, т.е.
. Тогда время контакта T равно половине периода собственных колебаний этой пружины, т.е.
![]() . (2)
. (2)
Если за нулевой момент времени принять момент начала соприкосновения мяча со щитом, то зависимость величины прогиба от времени описывается выражением:
X(t) = X0?sin(2π?f?t), (3)
где X0 – амплитуда прогиба.
Амплитуду прогиба X0 можно определить через равенство кинетической энергии движения и потенциальной энергии деформации:
![]() (4)
(4)
Зависимость радиуса пятна контакта от времени при принятых ранее допущениях будет выражаться следующей формулой:
![]() (5)
(5)
Примем следующие значения физических параметров для баскетбольного мяча размера 7 (средние значения из стандартных диапазонов, указанных в приложении):
M = 0.6 кГ, P = 8?104 Па, длина окружности 2?π?R = 0.77 м. Тогда ![]()
Коэффициент пропорциональности τ между величиной скорости V и амплитудой прогиба X0 в формуле (4) равен T/π = 0.00312. При скорости движения V = 10 м/с величина X0 равна 3.12 см; амплитуда радиуса пятна контакта r0 при этом будет равна 8.745 см.
Математическая модель процессов деформаций в твердых телах
Для изотропных материалов справочными параметрами, характеризующими их упругие свойства, являются модуль Юнга E, коэффициент Пуассона μ и модуль сдвига G, причем последний может быть вычислен через модуль Юнга и коэффициент Пуассона:
![]() . (6)
. (6)
Рассмотрим растяжение однородного стержня с площадью сечения S, ось которого совпадает с осью x1 системы координат. Растягивающая сила F создает единственную компоненту напряжения t1=F/S, которая вызывает деформации растяжения r1=S11t1 и r2=S21t1. С другой стороны, известно, что при условиях данной задачи r1 = t1/E, r2 = −μ?r1 и r3 = −μ?r1, откуда получаем:
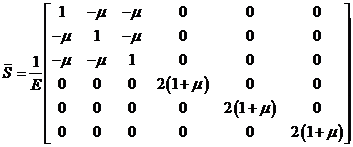 (7)
(7)
При решении задач расчета деформаций в качестве неизвестных параметров выступают компоненты перемещений, из которых выражаются деформации. Следовательно, напряжения необходимо выразить через деформации. С этой целью вычислим обратную матрицу ![]() :
:
 (8)
(8)
Эта матрица представляет собой тензор коэффициентов жесткости (коэффициентов упругости). Размерности компонентов тензора [н/м2]. Из выражений для тензора упругости видно, что коэффициент Пуассона μ не может превышать значения 0.5, а при значении 0.5 компоненты тензора обращаются в бесконечность. Такой случай соответствует несжимаемым материалам.
Уравнения, связывающие напряжения и деформации, будут выглядеть так: ![]() .
.
Введем в рассмотрение систему координат, в которой щит лежит в плоскости XY, а его толщина направлена вдоль оси Z. Щит можно рассматривать как тонкую пластину, поскольку его толщина много меньше длины и ширины. Тогда механические напряжения вдоль толщины можно считать равными нулю. В этом случае необходимо выразить компоненты деформаций в направлении оси Z через компоненты вдоль осей X и Y. Это легко сделать через компоненты тензора ![]() :
: ![]() . Подставляя это соотношение в выражения для напряжений, получаем:
. Подставляя это соотношение в выражения для напряжений, получаем:
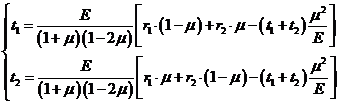 (9)
(9)
Вычислив сумму этих напряжений, получаем уравнение для суммы (t1+t2), решение которого легко найти:
![]() . (10)
. (10)
Подставляя это выражение в предыдущую систему уравнений, получаем:
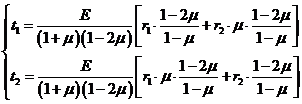 (11)
(11)
После учета этих соотношений и выполнения необходимых преобразований получаем следующую форму тензора упругости для плоского случая:
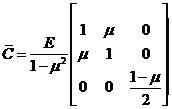 (12)
(12)
Поскольку от точки удара мяча распространяется круговая изгибная волна, задачу расчета деформаций необходимо сформулировать для осесимметричного случая, где ось симметрии проходит через центр удара перпендикулярно щиту. При этом будут использоваться только две компоненты смещений: Ur (в направлении, перпендикулярном оси симметрии) и Uz (в направлении вдоль оси симметрии). Расчет деформаций при этом производится в поперечном сечении пластины, проходящем через ось симметрии. Введем следующее обозначение осе координат для этого случая: ось Z направлена вдоль оси симметрии, ось R направлена перпендикулярно оси симметрии.
Для осесимметричных задач появляется дополнительная компонента деформации в направлении угловой координаты θ (перпендикулярная плоскости чертежа), которая связана с изменениями радиального размера: rθ = UR / R. Вектор деформаций имеет 4 компоненты и выглядит следующим образом:
![]()
Тензор упругости для осесимметричных задач равен:
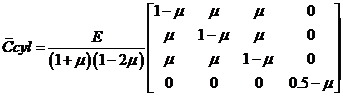 (13)
(13)
Для оценки времени распространения деформаций в листовом материале на основании приведенной математической модели был составлен дескрипторный файл описания задачи расчета переходных процессов для программы FlexPDE. Описание задачи было сделано для круглой пластины из оргстекла, закрепленной по краям, причем воздействие происходит в центре. Такая модель является правомочной для интервалов времени, при которых круговая изгибная волна еще не доходит до краев области и «не знает», что пластина круглая, а не прямоугольная. В этом случае задача является осесимметричной, и область решения существенно уменьшается. Расчеты проводились для круглого щита радиусом 90 см и толщиной 1 см. Контрольные точки находились на расстоянии 45 см от центра (точка «а»), и 80 см от центра (точка «б»). Обе точки лежали на глубине 0.5 см.
Результаты расчета скорости и ускорения в контрольных точках для такой модели приведены на рисунке 3.
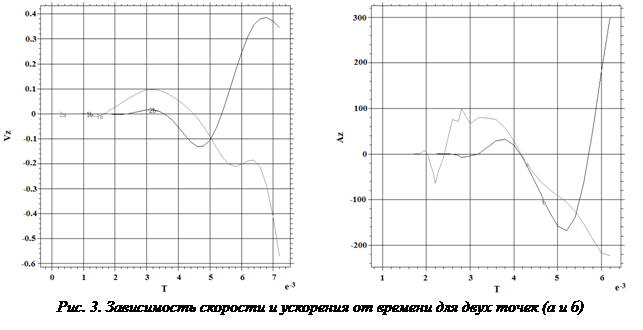
Из приведенных графиков видно, что скорость распространения изгибной цилиндрической волны не является постоянной. Это объясняется тем, что вблизи центра воздействия возникают деформации растяжения по окружности, которые спадают по мере удаления от центра. Эти деформации растяжения вносят вклад в общую энергию волны, и увеличивают эффективную жесткость системы вблизи центра воздействия.
Для более точного расчета распространения волны была использована программа Comsol Multiphysics [9]. В силу того, что толщина щита много меньше его длины и ширины, расчеты можно проводить с использованием теории Миндлина-Рейснера [10]. В программе Comsol Multiphysics имеется блок решения задач для тонких пластин (в этой программе такой тип задач называется «Mindlin Plate») в блоке «структурная механика».
Граничные условия для пластин могут быть заданы тремя различными способами:
1. Свободная граница (отсутствует закрепление).
2. Простое закрепление (смещения на границе отсутствуют, но крепление не мешает пластине поворачиваться вокруг оси, совпадающей с границей).
3. Жесткое закрепление (край пластины заделан в крепление так, что на границе отсутствуют смещения и повороты).
Первый тип граничных условий нельзя задавать по всей длине границы, т.к. в этом случае пластина сможет свободно двигаться в пространстве. Поэтому к пластине в расчетной модели были добавлены специальные «ушки», концы которых зафиксированы (по второму или третьему способу), что с физической точки зрения практически эквивалентно мягкому закреплению щита с помощью резиновых зажимов.
Результаты расчета Z – смещений в виде линий уровня (рельеф деформаций) приведены на рисунке 4. Область удара мяча изображена кругом большей толщины. Внутри этой области на щит действует давление мяча, причем радиус области давления меняется во времени по ранее рассмотренным формулам (4, 5).
При малых временах (порядка 1 мс) линии уровня представляют собой концентрические окружности с центром в точке удара мяча. Однако далее, по мере вовлечения краев щита в процесс деформаций, происходят существенные искажения симметрии распределения, хорошо видимые при Т > 2 мс.

Далее для значений сигналов в точках размещения датчиков был произведен экспорт данных во внешний файл, который затем был проанализирован в программе MathCad.
Сигнал на выходе датчика может зависеть от величины смещения (датчики положения), от скорости смещения (магнитные датчики, дифференцирующие датчики положения) и от ускорения (датчики ускорения). Но для однозначного определения координат точки удара необходимо, чтобы скорость распространения сигнала от точки удара до датчика была одинакова для всех датчиков.
Ниже производится попытка подбора коэффициентов распространения, при которых моменты времени прихода воздействия на датчик попадают на какие-либо характерные точки графика воздействия (точка максимума, перехода через ноль и т.п.) Для каждого графика используется свой коэффициент пропорциональности (рисунок 5). Маркерами отмечены моменты времени, пропорциональные задержке распространения волны от точки удара до соответствующих датчиков.

Как видно из последних рисунков, условие пропорциональности времени фиксации особых точек графиков величине расстояния от точки удара до датчика не выполняется. Не удается подобрать коэффициент распространения, при котором бы получались одинаковые параметры сигналов (максимумы, точки прохождения через нуль и т.п.).
Выводы
1. Перед построением системы измерений, основанной на распространении звуковых волн в щите, полезно произвести физическое моделирование процессов распространения этих волн с помощью современных программ конечноэлементного анализа.
2. При использовании акустических датчиков необходимо учитывать возможность распространения звуковых сигналов не только через сам щит, но и через элементы его крепления.
3. Гипотеза о постоянстве скорости концентрической изгибной волны в материале щита не является верной, поэтому использование метода акустической локации с помощью угловых датчиков ускорения для определения координат отскока мяча от щита при баскетбольных бросках на существующем спортивном оборудовании не представляется возможным.
Заключение
Отрицательный результат представленного исследования инициировал рассмотрение других методов измерения координат взаимодействия мяча с баскетбольным щитом, использующих другие физические принципы.
Конструкция нового баскетбольного щита и соответствующий метод измерения координат отражения мяча от щита при баскетбольных бросках будут представлены в следующих статьях.
Рецензенты:
Кравчук А.И., д.п.н, профессор кафедры теории и методики туризма и социально-культурного сервиса, «Сибирский государственный университет физической культуры и спорта», г. Омск;
Науменко А.П., д.п.н, доцент, начальник научно-учебного центра ООО «НПЦ «Динамика», г. Омск.
Библиографическая ссылка
Притыкин В.Н., Долганёв Ю.Г. ИСПОЛЬЗОВАНИЕ ДАТЧИКОВ АКУСТИЧЕСКИХ ВОЛН ДЛЯ ОПРЕДЕЛЕНИЯ КООРДИНАТ ОТРАЖЕНИЯ МЯЧА ОТ ЩИТА ПРИ БАСКЕТБОЛЬНЫХ БРОСКАХ // Современные проблемы науки и образования. 2015. № 1-2. ;URL: https://science-education.ru/ru/article/view?id=19893 (дата обращения: 26.02.2026).



