Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Инвариантное распознавание изображений является ключевым направлением в области распознавания образов. В настоящее время для инвариантного распознавания изображений наилучшие результаты показывают стохастические модели, а именно подкласс искусственных нейронных сетей (ИНС) – сверточные нейронные сети (СНС) [8]. Однако обучение ИНС – это плохо обусловленная (некорректная) обратная задача [5]. Плохая обусловленность означает, что даже большой набор данных может нести в себе малый объем информации о решении задачи. Поэтому ключевая роль в процессе синтеза параметров конкретной математической модели ИНС принадлежит обучающим данным. Составление же репрезентативной обучающей выборки является одной из самых сложных задач в машинном обучении [1; 5].

            Известно несколько альтернатив, применяемых вместо создания большой репрезентативной выборки, по расширению обучающего множества посредством добавления преобразованных паттернов.

1.        Использование специальных алгоритмов, которые перед обучением расширяют обучающее множество [7]. Однако настройка, подбор алгоритмов и получаемого размера множества становятся очень трудным этапом.

2.        Использование регуляризации [5]. Основной недостаток – более сложное обучение и трудность выработки устойчивости сети к требуемым искажениям.

3.        Изменение внутренних параметров математической модели сети [2]: искажения, накладываемые на вектор антиградиента, на настраиваемые веса сети, временное исключение некоторых нейронов или связей между ними во время обучения сети. Это позволяет решать в основном прикладные задачи: препятствовать переобучению, вырабатывать устойчивость работы сети к возможным отказам некоторых элементов. Увеличение обобщающей способности – лишь косвенное следствие применения подобных решений.

Предлагается за счёт изменения таких внутренних параметров СНС, как форма рецептивных полей (РП) [2], создавать искажения по отношению к текущему паттерну, тем самым получая новые паттерны и расширяя обучающую выборку [4; 9]. Для реализации предложенного подхода необходимо разработать алгоритм изменения формы РП для различных комбинаций сверточных слоёв СНС, а также метод синтеза параметров математической модели СНС с расширенным обучающим множеством, генерируемым изменением её РП.

Известный обобщённый алгоритм синтеза параметров для СНС включает в себя следующие шаги:

1.                  Подача и нормировка паттерна на вход СНС.

,                                      (1)

где   - новое значение входа нейрона, расположенного на карте i в позиции m, n после линейной нормировки.

2.                  Осуществление прямого прогона, т.е. распространение вычисляемых сигналов от входного слоя к выходному: на сверточном слое (С-слой) (2), на слое усреднения (S-слой) (3), выходном слое (4, 5) соответственно.

,                    (2)

,                           (3)

где , – выход нейрона, расположенного на i-й карте С или S-слоя в позиции m, n, φ(·) = A*tanh(B*p) при A=1.7159, B=2/3, p – взвешенная сумма, b – смещение, u – настраиваемый параметр для каждой S-карты (усредняющий коэффициент), Qi – множество индексов карт предыдущего слоя, связанных с картой Сi, KС, KS – размер квадратного РП для нейрона и  соответственно,  – входное значение для нейрона , – q-я часть настраиваемых параметров, которая отвечает за взаимодействие с q-й картой предыдущего слоя.

,                                                    (4)

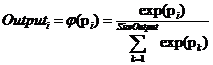,                                         (5)

            где i = 1..SizeOutput, SizeOutput – кол-во нейронов в выходном слое, K – кол-во нейронов в слое, предшествующем выходному слою (вырожденный С-слой), wi,k – настраиваемые параметры выходного слоя, bi – смещение для нейрона этого слоя, pi – взвешенная сумма нейронов этого слоя, Outputi – выход i-го нейрона выходного слоя.

3.                  Вычисление ошибки на выходном слое.

,                                             (6)

            где  – k-й элемент вектора-учителя.

4.                  Осуществление обратного прогона.

Для выходного слоя (7), для вырожденного слоя (8), для S-слоёв (9, 10), для С-слоёв (11, 12), для смещений (13) соответственно.

,                                                    (7)

            где – локальный градиент (невязка), получаемая на выходном слое, который далее распространяется от выхода к входу, λ – номер слоя, – настраиваемые параметры для λ слоя,  – выходное значение нейрона j со слоя λ-1.

,            (8)

где D – множество нейронов из последующего слоя (λ-слой), соединённых с нейроном ,  производная от ,

Для C-слоя и S-слоя вычисление компонентов вектора градиента происходит в два этапа: сначала вычисляется накопленная невязка, затем сам компонент вектора градиента по параметру сети.

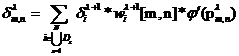,                                        (9)

            где  – невязка, собираемая для нейрона с координатами m, n в пределах карты слоя λ,  – настраиваемый параметр для связи, соединяющий нейрон m, n на S-слое и нейрон с невязкой , , (∆t, ∆z) – смещение в рамках ядра для настраиваемого параметра связи, N – кол-во карт, которые связаны с текущим нейроном из последующего слоя, Dz – множество связанных нейронов последующего слоя из z-й карты, которые связаны с нейроном m, n.

,                                              (10)

            где , т.к. ,  SizeS – размер карты S-слоя.

,                                   (11)

            где D – множество нейронов на последующей карте (λ+1 слой), связанных с нейроном n, m,  – это  той карты S-слоя, с которой связана карта С-слоя.

,                                      (12)

            где q – та часть ядра настраиваемых параметров, для которых получают компонент градиента, SizeC – размер карты С-слоя.

Обновления смещений для S-слоёв и C-слоёв происходят по формуле (13)

,                                                  (13)

где  – компонент вектора градиента для смещения i-й S или C-карты слоя λ, SizeCard – размер карты С-слоя или S-слоя, если происходит обновление смещения для C-слоя или S-слоя соответственно.

5.      Корректировка настраиваемых параметров СНС.

,                                           (14)

где wnew, wold – значения новых и старых параметров соответственно, η –

скорость обучения, – вектор градиента.

Известно, что классическая форма РП в СНС – это квадрат [8]. Для получения нестандартного РП предлагается использовать шаблон, элементами которого являются индексы [9], обозначающие своих соседей в пределах двух дискретных шагов от них на пиксельной матрице. При изменении всех РП, лежащих на карте, на настраиваемые параметры будет воздействовать дополнительная информация, что приведёт к выделению лучшего инварианта (рис. 1).

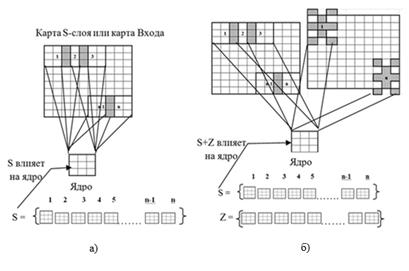
Рис. 1:  а) стандартные РП, б) стандартные и добавочные РП

Вектор антиградиента, получаемый при использовании нестандартных РП, в контексте процесса обучения можно рассматривать как наложение искажений на вектор антиградиента, получаемый при использовании стандартных РП.

Использование РП нестандартной формы требует адаптации алгоритма обратного распространения ошибки на шаге 2 и 4: предлагается вместо формул (2) и (12) использовать формулы (15) и (17) соответственно.

,            (15)

где , – функции, возвращающие смещения по строке и столбцу для шаблона РП, принадлежащего нейрону m,n в позиции k, l внутри этого шаблона.  – есть элемент шаблона  в позиции k, l, . Данные функции определяются по следующим формулам:

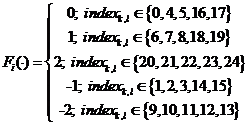
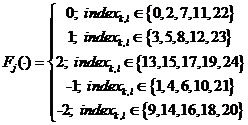  ,       (16)                                  

,                  (17)

Предлагается алгоритм, изменяющий перед подачей паттерна РП у нейронов, лежащих на любой комбинации С-слоёв. Информация о таком изменении берётся из столбцов матрицы A9xL.

,                                                               (18)

где L – количество столбцов матрицы A, N0 – количество паттернов в искомой обучающей выборке, M – количество добавленной информации о смене РП для преобразования M паттернов.

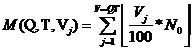,                                                     (19)

            где Q – количество комбинаций С-слоёв, которые могут иметь или не иметь РП нестандартной формы. Использовались СНС с тремя С-слоями, поэтому конкретная комбинация представляет собой набор трёх цифр: ,                                                    , i=1..2(Кол-во С-слоёв), T – количество тактов, Vj – целое число, обозначающее процент от N0, 0≤ Vj ≤100, V – кол-во чисел Vj, V=TQ.

Каждый С-слой может иметь несколько типов РП: , где SetRPi – множество типов РП для i-го С-слоя, RP1 – квадратное РП, ni – количество типов РП для i-го С-слоя.

Для присвоения нейронам i-го C-слоя РП предлагается использовать два алгоритма. Алгоритм  присваивает всем нейронам слоя Сi РП с индексом RPt, t=1..T ­– номер такта, T=ni. Такой алгоритм при соответствующих РП обеспечивает инвариантность к сдвигам, алгоритм– присваивает каждому нейрону из слоя Ci случайное поле RP из SetRPi. Такой алгоритм обеспечивает инвариантность к локально-аффинным преобразованиям типа elastic distortions [3]. Инвариантность к масштабу, текстурам фона, положению объекта, уровням освещённости обеспечивается исходной обучающей выборкой.

Поскольку свои РП могут иметь любые С-слои, то алгоритмы разметки слоя могут быть использованы алгоритмами разметки всех C-слоёв. Предлагается два таких алгоритма:

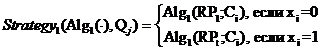,                           (20)

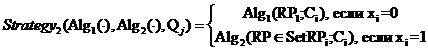,                  (21)

где i=1... количество С-слоёв, , 1 ≤ t ≤ T = ni, Qj – конкретная комбинация С-слоёв, которые имеют или не имеют РП нестандартной формы.

Обобщённый алгоритм изменения формы РП для слоёв СНС представлен на рисунке 2.

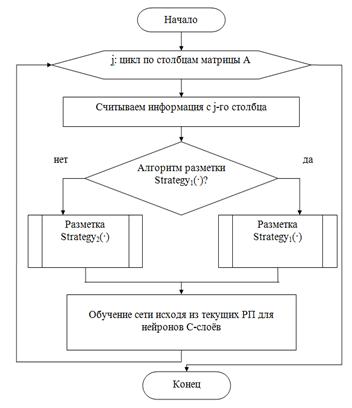
Рис. 2. Обобщённый алгоритм изменения формы рецептивных полей для слоёв СНС

Разработанный  алгоритм синтеза параметров математической модели СНС с расширенным обучающим множеством представлен на рисунке 3.

 

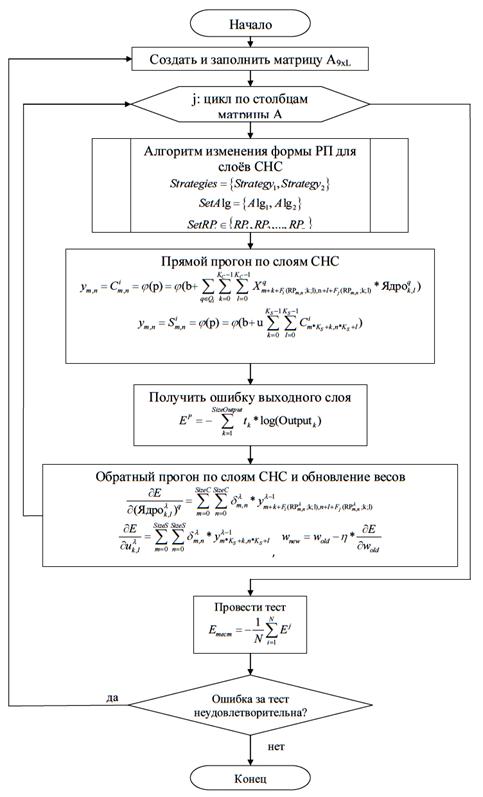
Рис. 3. Обобщённый алгоритм синтеза параметров математической модели СНС с расширенным обучающим множеством, генерируемым изменением её РП

Эксперименты по оценке обобщающей способности предлагаемой математической модели СНС с расширенным обучаемым множеством проводились с использованием трёх выборок: MNIST (рукописные цифры) [10], Small NORB (пять классов объектов) [11], выборка, созданная для распознавания 10 классов объектов со стенда «Мехатроника» [3].

Результаты вычислительных экспериментов представлены в таблице 1.

Таблица 1

Результаты вычислительных экспериментов по оценке обобщающей способности алгоритма обучения СНС предлагаемым способом и влияния редукции на процесс обучения

Из таблицы следует, что обучение СНС с помощью предлагаемого метода улучшает в среднем обобщающую способность сети на 2.5%. Численный метод редукции [4] расширенного обучающего множества позволяет сократить время обучения в среднем на 9 ч, что составляет 37% от первоначального времени обучения без редукции.

Для распознавания объектов со стенда «Мехатроника» [6] разработан программный комплекс, позволяющий распознавать объекты с камер мобильного робота. Комплекс состоит из двух модулей: выделение потенциально интересных мест на кадре и распознавание выделенных изображений, переданных на вход СНС. Оболочка комплекса и алгоритм выделения мест написаны на С#, распознавание с помощью СНС реализовано на C++ и подключается в виде библиотеки к основной программе.

Эксперименты с распознаванием объектов на стенде «Мехатроника» для различных расстояний от камеры (AXIS M1054) приведены в таблице 2.

Таблица 2

Процент правильных распознаваний для экспериментов на стенде «Мехатроника» при использовании предлагаемой математической модели СНС и в скобках без неё

Объект/Расстояние от камеры	50 см	1 м	1.5 м (расстояние до стола)	2 м
Мяч	93% (80%)	91% (75%)	87% (66%)	78% (63%)
Мотоцикл	91% (85%)	87% (79%)	88% (74%)	75% (69%)
Машина	89% (81%)	85% (77%)	82% (71%)	68% (67%)
Фонарь	94% (82%)	90% (71%)	92% (65%)	72% (59%)
Лягушка	95% (79%)	91% (78%)	89% (60%)	69% (59%)
Самолёт	91% (84%)	90% (72%)	87% (67%)	74% (65%)
Плеер	90% (79%)	89% (77%)	90% (63%)	75% (58%)
Тыква	85% (81%)	83% (71%)	80% (68%)	63% (63%)
Солдат	96% (85%)	92% (76%)	90% (64%)	73% (60%)
Степлер	92% (78%)	89% (64%)	88% (62%)	71% (59%)
Пустой класс	98%	98%	98%	96%

Из полученных результатов следует, что точность распознавания для объектов достигает 96% при использовании метода синтеза параметров математической модели СНС с расширенным обучающим множеством. С увеличением расстояния от камеры точность распознавания падает из-за ухудшающегося качества входного изображения. На расстоянии больше 2 м происходит выделение слишком большого количества потенциально интересных мест и распознавание в реальном времени становится невозможным. Обученная СНС может быть перенесена на мобильного робота AR-601E, где способна стать ядром  системы его технического зрения.

Рецензенты:

Лубенцов В.Ф., д.т.н., профессор, заместитель директора по научной работе Невинномысского технологического института (филиал) ФГАОУ ВПО «Северо-Кавказский федеральный университет» Минобрнауки РФ, г. Невинномысск;

Дроздова В.И., д.ф.-м.н., профессор, заведующая кафедрой информационных систем и технологий Института информационных систем и телекоммуникаций ФГАОУ ВПО «Северо-Кавказский федеральный университет» Минобрнауки РФ, г. Ставрополь.