В основе большинства методов решения многокритериальных задач заложен принцип сведения их к однокритериальным. Для достижения этой цели существует ряд приёмов.
Одним из простейших приёмов сведения многокритериальной задачи к однокритериальной является выделение среди множества показателей эффективности какого-либо одного (самого главного). В дальнейшем оптимизация ведётся по этому единственному критерию, а остальные показатели эффективности ограничиваются сверху или снизу и служат ограничениями.
Пусть, например, необходимо максимизировать m критериев:
![]() (1)
(1)
Выбираем среди этих m критериев главный
(например, ![]() ), а остальные
ограничиваем снизу величинами
), а остальные
ограничиваем снизу величинами ![]() ,
, ![]() . Задача при этом
принимает вид:
. Задача при этом
принимает вид:
![]() (2)
(2)
При использовании этого способа возникают две трудности. Во-первых,
не всегда удаётся выделить среди множества критериев самый главный, а во-вторых,
часто не ясно, из каких соображений ограничивать остальные критерии величинами ![]() .
.
Одним из самых распространённых методов сведения многокритериальных задач к однокритериальным является использование составных критериев. Здесь наблюдаются разные подходы. Иногда максимизируют сумму критериев:
![]() , (3)
, (3)
иногда их произведение:
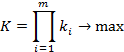 (4)
(4)
В некоторых случаях в составных критериях используют «весовые» коэффициенты. Например:
![]() , (5)
, (5)
где ![]() «вес» (важность) i-го показателя эффективности. Если часть критериев необходимо
максимизировать (например, первые q критериев), а
оставшиеся (m-q) критериев надо минимизировать, то используют дробь:
«вес» (важность) i-го показателя эффективности. Если часть критериев необходимо
максимизировать (например, первые q критериев), а
оставшиеся (m-q) критериев надо минимизировать, то используют дробь:
![]() (6)
(6)
Существуют и другие способы образования составного критерия. Все они имеют общий недостаток: при использовании таких критериев недостаток в одном критерии может быть скомпенсирован за счёт другого. Например, максимизируя сумму критериев, может получиться, что один из них будет иметь маленькое значение, а другой большое. И хотя их сумма будет достаточно велика, полученное решение нельзя считать хорошим.
Все окружающие нас процессы управления представимы в виде многоуровневой иерархической системы. На каждом уровне решаются свои задачи по своим критериям. Информация, выработанная на k-м уровне, поступает на (k+1)-й уровень, где используется для решения других задач по другим критериям и т.д. При переходе от уровня к уровню, как правило, сокращается число решаемых задач, но значительно возрастает их важность и сложность. Таким образом, иерархическая система управления напоминает пирамиду, рассечённую множеством плоскостей, параллельных основанию. Каждая из таких плоскостей соответствует определённому уровню управления. В основании этой пирамиды (низший уровень) лежат обычно простейшие задачи оперативного управления.
Критерии задач k-го уровня должны быть согласованы с интересами (k+1)-го уровня управления. Это обстоятельство часто помогает при выработке рекомендаций в условиях многокритериальности. Действительно, если в такой ситуации подняться на более высокий уровень, то становится ясным, каким критериям следует отдать предпочтение. Переход на более высокий уровень управления позволяет решить ещё одну проблему – правильную оценку коэффициентов относительной важности в составных критериях.
Рассмотрим теперь методы определения множества Парето.
Пусть необходимо выбрать решение некоторой задачи по двум
показателям эффективности: ![]() и
и ![]() (причем каждый из этих
критериев должен быть, по возможности, максимальным, т.е.
(причем каждый из этих
критериев должен быть, по возможности, максимальным, т.е. ![]() и
и ![]() ). Изобразим все
возможные решения этой задачи в виде некоторого замкнутого множества M, рассматриваемого на плоскости с осями координат
). Изобразим все
возможные решения этой задачи в виде некоторого замкнутого множества M, рассматриваемого на плоскости с осями координат ![]() и
и ![]() (рис. 1).
(рис. 1).
Каждая точка множества М соответствует одному из решений,
которое характеризуется значениями критериев ![]() и
и ![]() . Как видно, некоторые
из этих решений очень похожи. Например, решение, отмеченное точкой a, характеризуется очень маленькими значениями каждого из
критериев. Решение, отмеченное точкой d, лучше решения a по критерию
. Как видно, некоторые
из этих решений очень похожи. Например, решение, отмеченное точкой a, характеризуется очень маленькими значениями каждого из
критериев. Решение, отмеченное точкой d, лучше решения a по критерию ![]() , но уступает ему по
критерию
, но уступает ему по
критерию ![]() . Стремление
максимизировать решение по критерию
. Стремление
максимизировать решение по критерию ![]() приводит к выбору точки
b, а максимальное значение критерия
приводит к выбору точки
b, а максимальное значение критерия ![]() достигается при выборе
решения, которому соответствует на рис. 1 точка c.
достигается при выборе
решения, которому соответствует на рис. 1 точка c.
Очевидно, что все наилучшие решения расположены на участке
дуги ![]() . Действительно, любое
другое решение, находящееся вне этой дуги, может быть улучшено по крайней мере
по одному показателю (а для большинства решений – сразу по двум). Участок
. Действительно, любое
другое решение, находящееся вне этой дуги, может быть улучшено по крайней мере
по одному показателю (а для большинства решений – сразу по двум). Участок ![]() носит название «множество
эффективных планов» или «множество Парето» и характеризуется тем важным
свойством, что на нем ни одно решение не может быть улучшено по одному из
критериев без ущерба для другого критерия.
носит название «множество
эффективных планов» или «множество Парето» и характеризуется тем важным
свойством, что на нем ни одно решение не может быть улучшено по одному из
критериев без ущерба для другого критерия.
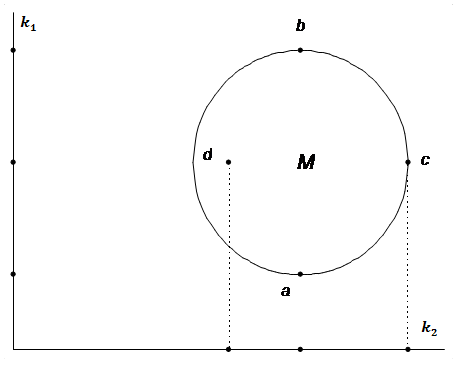
Рис. 1. Множество Парето
В общем случае определение областей Парето в многокритериальных задачах связано с преодолением значительных трудностей. Однако в некоторых ситуациях удается довольно просто находить такие области. Ниже рассматривается графоаналитический метод нахождения множества эффективных планов для задачи линейного программирования с одним ограничительным условием и двумя критериями эффективности:
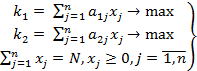 (7)
(7)
Рассмотрим метод решения задачи (1) на следующем числовом примере:
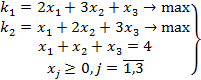 (8)
(8)
Задавая последовательно каждой переменной значение 4, получаем три точки
треугольника АВС на плоскости с
осями координат ![]() и
и ![]() (рис. 2).
(рис. 2).
Очевидно, что все допустимые решения этого примера находятся внутри треугольника АВС и на его границах. Очевидно также, что множество эффективных планов (наилучших решений) находится на отрезке ВС.
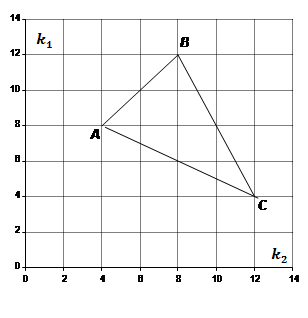 |
 Рис. 2. Множество Парето для задачи
(2)
Рис. 2. Множество Парето для задачи
(2)
Воспользуемся выражением уравнения прямой, проходящей через две точки (![]() ) и (
) и (![]() ):
):
![]()
и составим аналитическое выражение, описывающее множество Парето в рассматриваемом примере (иначе говоря, составим уравнение отрезка ВС):
![]()
Как
видно, критерий ![]() может принимать любое
значение из замкнутого интервала [4; 12]. Выбор значения
может принимать любое
значение из замкнутого интервала [4; 12]. Выбор значения ![]() однозначно определяет
значение второго критерия
однозначно определяет
значение второго критерия ![]() . Например, если
задаться для
. Например, если
задаться для ![]() значением 10, то
значением 10, то ![]() будет равным 9, если
будет равным 9, если ![]() = 8, то
= 8, то ![]() = 10 и т.д.
= 10 и т.д.
В приведенном примере область Парето представляет собой отрезок прямой линии. В общем случае таких отрезков может быть несколько (множество эффективных планов выражается кусочно-линейной функцией). Рассмотрим следующий пример:
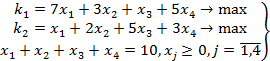 (9)
(9)
Присваиваем
последовательно каждой переменной значение 10 и вычисляем критерии ![]() и
и ![]() . При
. При ![]() =10,
=10, ![]() =70 и
=70 и ![]() =10, при
=10, при ![]() =10,
=10, ![]() =30 и
=30 и ![]() =20 и т.д. Полученные
точки откладываем на плоскости в осях координат
=20 и т.д. Полученные
точки откладываем на плоскости в осях координат ![]() и
и ![]() (рис. 3).
(рис. 3).
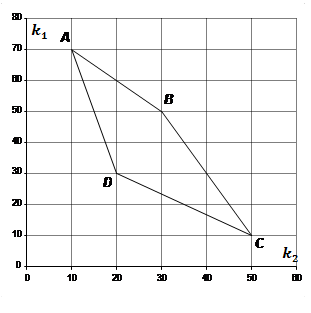
Рис.
3. Множество Парето для задачи (3).
Очевидно, что все допустимые решения примера (3) находятся внутри четырехугольника ABCD и на его границах, а наилучшие решения – на отрезках АВ и ВС. Составим аналитические выражения, описывающие множества Парето в рассматриваемом примере. Для отрезка АВ
![]()
а для отрезка ВС
![]()
Как
видно, на отрезке АВ полученного
множества Парето критерий ![]() не может быть больше
30. Если этого недостаточно, то можно перейти на отрезок ВС. Однако на этом отрезке критерий
не может быть больше
30. Если этого недостаточно, то можно перейти на отрезок ВС. Однако на этом отрезке критерий ![]() не может быть больше
50. В зависимости от степени важности критериев следует предпочтение отдавать
тому или иному отрезку множества Парето.
не может быть больше
50. В зависимости от степени важности критериев следует предпочтение отдавать
тому или иному отрезку множества Парето.
Рецензенты:
Максаров В.В., д.т.н., профессор, заведующий кафедрой машиностроения, ФГБОУ ВПО «Национальный минерально-сырьевой университет «Горный», г. Санкт-Петербург;
Михайлов А.В., д.т.н., профессор кафедры машиностроения, ФГБОУ ВПО «Национальный минерально-сырьевой университет «Горный», г. Санкт-Петербург.
Библиографическая ссылка
Терентьев А.В. МЕТОДЫ РЕШЕНИЯ АВТОТРАНСПОРТНЫХ ЗАДАЧ // Современные проблемы науки и образования. 2015. № 1-2. ;URL: https://science-education.ru/ru/article/view?id=19863 (дата обращения: 01.02.2026).



