Следует отметить, что в настоящий период в системных исследованиях познавательной деятельности разработаны различные аспекты интегральных концепций и интегративных подходов к обучению математике: психологический аспект (А.Г.Асмолов, Г.А.Балл, Э.Е.Бехтель, Дж. Брунер, П.Я.Гальперин, В.А.Ганзен и др.)[1; 2]; культурологический аспект (А.Ю.Большакова, А.В.Волошинов, Т.В.Иванова, Е.А.Перминов, А.Е.Чучин-Русов и др.)[3; 5; 6]; философский аспект (Ю.С.Владимиров, В.С.Меськов, А.А.Мамченко, В.С.Степин, О.Ф.Теребилов, С.К.Черепанов, В.А.Штофф, В.А.Яковлев и др.)[4; 9]; подход прогрессивно-технологического обучения (Е.З.Власова, Г.Л.Ильин, В.М.Монахов, В.А.Сластенин и др.) [8]; интегративный подход (В.Н.Воронин, В.А.Далингер, А.Я.Данилюк, И.Ю.Дик, Н.К.Чапаев и др.)[5].
В связи с этим в математическом образовании следует актуализировать методику и методы комплексного подхода к обучению математике, построенного на основе комплексного (интегрального) мышления, имеющего триадическую структуру (математическое, диалектическое, жизнедеятельностное), и выделенных нами основных методологических принципов[10]. Такой подход в обучении математике позволяет выявить структурные единицы, которые находятся в однозначном соответствии с аналогичными структурами в других разделах математики, и выделить общие логические схемы. В этих схемах по определенному логическому плану устанавливается соответствие между основными понятиями алгебраических, геометрических и логических структур и фундаментальными понятиями физических структур. Выявление такой связи структур имеет важное значение в обучении математике с точки зрения целостного восприятия объекта исследования и долговременного запоминания этих связей в формализованном виде.
Таким образом, определенные логические схемы (мнемосхемы), связывающие понятия структур различных предметных областей в единое целое, имеют важное значение в мнемической деятельности и практике применения полученных знаний для решения задач прикладного характера.
Под мнемической деятельностью понимается активная деятельность человека, направленная на запоминание и воспроизведение материала, а мнемосхема определяется как графическая информационная модель, условно отображающая функционально-техническую схему управляемого объекта и информацию о его состоянии в объеме, необходимом для выполнения оператором возложенных на него функций [7].
Цель исследования: на основе фундаментальных понятий различных разделов математики выявить общие закономерности взаимодействия элементов соответствующих структур (синергизм) и логическую схему метапредметного содержания (мнемосхему), на основе которых строится мнемическая деятельность, ориентированная на долгосрочное запоминание основных формализованных связей базисных компонентов моделей представления знаний междисциплинарного характера и на формирование общекультурных и профессиональных компетенций.
Формирование приемов смысловой, логической обработки запоминаемого материала рассматривается как основной путь не только повышения эффективности работы памяти, но и развития логической составляющей мышления, столь важной при обучении математике, и воспитания культуросообразной личности, способной целостному восприятию изучаемого предмета. Здесь мы укажем на некоторую систему различных приемов и методов, облегчающих запоминание и увеличивающих объем памяти и знаний путем образования искусственных ассоциаций (мнемоника, мнемотехника). Запоминание определенного материала происходит различными языковыми средствами, способствующими активизации и интегрированию процессов, служащих средством воспроизведения знаний об одном и том же объекте на различных изоморфных математических моделях.
Поясним предлагаемую процедуру мнемической деятельности при обучении математике в педагогическом вузе для физико-математических специальностей на конкретных примерах. Она же, очевидно, в несколько ином виде применима при обучении математике студентов технических и даже гуманитарных специальностей.
Один из основных объектов геометрии – прямая - почти во всех пособиях по высшей математике обычно представляется общим уравнением в виде
Ах + Ву + С = 0. (1)
Это уравнение и другие его разновидности получают, пользуясь свойствами коллинеарности или перпендикулярности текущего вектора, направляющего вектора и вектора нормали прямой. Перепишем уравнение (1) в виде
Ах + Ву = - С. (2)
Тогда левую часть этого уравнения можно интерпретировать как скалярное произведение текущего вектора ОМ(х,у) и вектора нормали n(А,В), а сама прямая определяется при этом как множество точек плоскости, каждая из которых сохраняет скалярное произведение векторов ОМ и n постоянным и равным – С. Механически левая часть уравнения (2) представляет собой работу силы F = ОМ на перемещение точки прямой на вектор n. Тогда прямая (2) определяется как множество точек плоскости, каждая из которых под действием силы ОМ, перемещаясь на вектор n, совершает одну и ту же работу, равную – С. Итак, прямая определяется через скалярное произведение, обладающее свойством коммутативности.
Теперь представим уравнение (2) в виде
![]() = - C. (3)
= - C. (3)
Левая часть уравнения (3) представляет собой площадь параллелограмма, построенного на векторах ОМ (х,у) и р (- В,А) – направляющего вектора прямой, т.е. абсолютные значения левой и правой частей уравнения (3) равны длине векторного произведения векторов ОМ и р. Механически эта длина совпадает с длиной момента количества движения точки единичной массы относительно точки О, т.е. │[ОМ,р]│. Тогда прямая на плоскости представляется и как множество точек, для каждой из которых площадь параллелограмма, построенного на векторах ОМ и р, постоянна и равна – С, и как множество точек плоскости, для каждой из которых длина момента количества движения относительно точки О постоянна и равна │-С│= │С│.
Таким образом, прямую на плоскости можно интерпретировать на разных моделях представления как с помощью скалярного произведения (симметрическая операция), так и с помощью векторного произведения (кососимметрическая операция). В обучении математике такая двойственность понятий позволяет глубже понять сущностную связь интенциального и реального, абстрактного и эмпирического, идеального и материального.
Суммируя высшесказанное, выделим
мнемосхему следующим образом. Из координат векторов плоскости х (![]() )
и у (
)
и у (![]() )
построим матрицу Х =
)
построим матрицу Х = ![]() ,
и ей ставим в соответствие сначала билинейную симметрическую форму (форма
скалярного произведения) как сумму произведений элементов соответствующих
строк
,
и ей ставим в соответствие сначала билинейную симметрическую форму (форма
скалярного произведения) как сумму произведений элементов соответствующих
строк ![]() (х,у) =
(х,у) = ![]() (у,х) =
(у,х) = ![]() ,
а затем – билинейную кососимметрическую форму (форма векторного произведения,
или площади) как
,
а затем – билинейную кососимметрическую форму (форма векторного произведения,
или площади) как ![]() (х,у) = -
(х,у) = -![]() (у,х) =
(у,х) = ![]() -
-
![]() =
- (
=
- (![]() -
-
![]() ).
Первую схему обозначим через А и назовем схемой скалярного произведения (или
длины, расстояния), а вторую схему обозначим через В и назовем схемой
векторного произведения (или внешнего произведения, или площади).
).
Первую схему обозначим через А и назовем схемой скалярного произведения (или
длины, расстояния), а вторую схему обозначим через В и назовем схемой
векторного произведения (или внешнего произведения, или площади).
Применим эти схемы для запоминания определенных формул из математического анализа и теории поля, играющих важную роль для решения задач физического характера.
Пусть ![]() ,
,![]() -
координаты некоторого касательного вектора на плоскости и dx,dy – координаты соответствующего
ковектора, а Р (х,у) , Q (х,у) – непрерывно дифференцируемые по
х,у функции. Составим матрицы
-
координаты некоторого касательного вектора на плоскости и dx,dy – координаты соответствующего
ковектора, а Р (х,у) , Q (х,у) – непрерывно дифференцируемые по
х,у функции. Составим матрицы ![]() ,
,
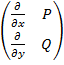 .
Первой матрице по схеме А соответствует дифференциальная форма Pdx +Qdy, а второй матрице по схеме В
соответствует форма площади
.
Первой матрице по схеме А соответствует дифференциальная форма Pdx +Qdy, а второй матрице по схеме В
соответствует форма площади ![]() .
Пусть G – односвязная область на плоскости
(ХОУ) с границей
.
Пусть G – односвязная область на плоскости
(ХОУ) с границей ![]() Тогда
интеграл от формы Pdx + Qdy вдоль границы области G равен двойному интегралу от формы
площади по G, т.е. имеем известную формулу Грина
Тогда
интеграл от формы Pdx + Qdy вдоль границы области G равен двойному интегралу от формы
площади по G, т.е. имеем известную формулу Грина![]()
![]() (4)
(4)
Обобщим эти
схемы в трехмерном пространстве ![]() .
Следует заметить, что первая схема обобщается в евклидовых пространствах любой
размерности, а вторая схема – в симплектических пространствах.
.
Следует заметить, что первая схема обобщается в евклидовых пространствах любой
размерности, а вторая схема – в симплектических пространствах.
Итак, пусть Х = 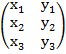 -
матрица, составленная из координат векторов х(
-
матрица, составленная из координат векторов х(![]() .
По схеме А матрице Х соответствует форма
.
По схеме А матрице Х соответствует форма ![]() +
+
![]() а
по схеме В ей соответствует форма с компонентами
а
по схеме В ей соответствует форма с компонентами ![]()
Пусть кривая ![]() с
указанным выше условием ограничивает некоторую поверхность F в пространстве
с
указанным выше условием ограничивает некоторую поверхность F в пространстве ![]() и P(x, y, z), Q(x, y, z), R(x, y, z) – непрерывно дифференцируемые по x, y, z функции. По аналогии вышеуказанной
процедуры составим матрицы
и P(x, y, z), Q(x, y, z), R(x, y, z) – непрерывно дифференцируемые по x, y, z функции. По аналогии вышеуказанной
процедуры составим матрицы
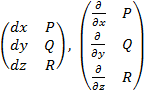 .
По схеме А первой матрице соответствует дифференциальная форма Pdx + Qdy + Rdz, а второй матрице по схеме В
соответствует форма с компонентами
.
По схеме А первой матрице соответствует дифференциальная форма Pdx + Qdy + Rdz, а второй матрице по схеме В
соответствует форма с компонентами ![]() ,
т.е. дифференциальная 2–форма – форма площади. Формально эти компоненты
получаются вычеркиванием во второй матрице соответственно первой, второй и
третьей строк, а затем из оставшихся строк по схеме В составляется форма
площади. Окончательно имеем форму
,
т.е. дифференциальная 2–форма – форма площади. Формально эти компоненты
получаются вычеркиванием во второй матрице соответственно первой, второй и
третьей строк, а затем из оставшихся строк по схеме В составляется форма
площади. Окончательно имеем форму
Интегрируя дифференциальную форму, полученную по схеме А, вдоль границы поверхности F и дифференциальную форму, полученную по схеме В, по поверхности F, имеем известную формулу Гаусса – Остроградского
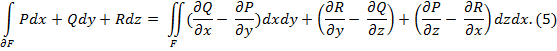
Более того, механически формула (5)
означает, что циркуляция векторного поля с координатами P,Q,R вдоль замкнутого контура ![]() (или
работа силы F
(P,Q,R) при перемещении точки вдоль
(или
работа силы F
(P,Q,R) при перемещении точки вдоль ![]() )
равна потоку вихря (ротора) с указанными выше компонентами через поверхность G, ограниченную контуром
)
равна потоку вихря (ротора) с указанными выше компонентами через поверхность G, ограниченную контуром ![]() .
Если же ротор обращается в нулевой вектор, то это означает, что
соответствующее поле F
(P,Q,R) является потенциальным. По схеме А
второй матрице соответствует скаляр
.
Если же ротор обращается в нулевой вектор, то это означает, что
соответствующее поле F
(P,Q,R) является потенциальным. По схеме А
второй матрице соответствует скаляр ![]() +
+
![]() +
+
![]() ,
равный дивергенции вектора F
(P,Q,R). Потенциальное поле с нулевой
дивергенцией является соленоидальным.
,
равный дивергенции вектора F
(P,Q,R). Потенциальное поле с нулевой
дивергенцией является соленоидальным.
Замечание. В левых частях равенств (4) и (5)под
интегралами стоят дифференциальные 1–формы, а в правых частях – их
дифференциалы, т.е. дифференциальные 2–формы. В общем случае связь междук–формой Ω и ее
дифференциалом dΩ для любого ориентируемого
многообразия М с краем![]() устанавливается
формулой Стокса, определяемой в виде
устанавливается
формулой Стокса, определяемой в виде
![]() .
(6)
.
(6)
Наконец, рассмотрим некоторые
разновидности этих схем. Пусть задана аналитическая функция f(z) = u(x, y) + iv(x, y). Применяя к функциям u(x, y), v(x, y), непрерывно дифференцируемым по х, у в
некоторой замкнутой области, схемы А и В относительно матрицы 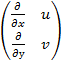 ,
в несколько иной форме, получим равенства
,
в несколько иной форме, получим равенства ![]() Эти
равенства на самом деле определяют условия дифференцируемости функции
комплексной переменной f(z). (Их называют уравнениями Коши –
Римана или Даламбера – Эйлера.) На основе этих уравнений и формулы Грина
доказывается одна из центральных теорем комплексного анализа – интегральная
теорема Коши, с помощью которой получаем интегральную формулу Коши. Эта
формула, в свою очередь, позволяет разложить аналитическую функцию в ряды
Тейлора и Лорана. Тем самым мнемосхемы А и В дают почти полную информацию о
содержании основного курса комплексного анализа.
Эти
равенства на самом деле определяют условия дифференцируемости функции
комплексной переменной f(z). (Их называют уравнениями Коши –
Римана или Даламбера – Эйлера.) На основе этих уравнений и формулы Грина
доказывается одна из центральных теорем комплексного анализа – интегральная
теорема Коши, с помощью которой получаем интегральную формулу Коши. Эта
формула, в свою очередь, позволяет разложить аналитическую функцию в ряды
Тейлора и Лорана. Тем самым мнемосхемы А и В дают почти полную информацию о
содержании основного курса комплексного анализа.
Заключение. Таким образом, мнемосхема, подчиненная определенной логико-конструктивной деятельности, связывающей основные понятия алгебры, геометрии и теории функций, дает возможность более эффективно разрешить проблему структурирования содержания образования того или иного раздела математики в направлении выявления более общих закономерностей и синтеза методов исследования в различных предметных областях знаний. Построение таких схем должно быть ориентировано на развитие комплексного мышления, способствующего формированию у студентов целостно структурированных знаний об окружающем мире и восприятию фрактальных эффектов в нелинейных системах. Мнемосхемы строятся в соответствии с логическими законами метапредметного содержания, и поэтому мнемическая деятельность на самом деле входит в метапредметную деятельность, а под метапредметным содержанием, в свою очередь, понимается освоение универсальных учебных действий, а также универсальных способов мышления и действий, не являющихся специфическими для предметного материала.
Рецензенты:Везиров Т.Г, д.п.н., профессор, профессор кафедры методики преподавания математики и информатики Дагестанского государственного педагогического университета, г. Махачкала;
Сурхаев М.А. д.п.н., профессор, профессор кафедры информационных и коммуникационных технологий Дагестанского государственного педагогического университета, г. Махачкала.
Библиографическая ссылка
Ярахмедов Г.А., Абдуразаков М.М., Казибеков Т.Л. О МНЕМИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ В КОМПЛЕКСНОЙ МОДЕЛИ ОБУЧЕНИЯ МАТЕМАТИКЕ В ВУЗЕ // Современные проблемы науки и образования. 2015. № 1-2. ;URL: https://science-education.ru/ru/article/view?id=19862 (дата обращения: 26.02.2026).



