Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Известные конструкции намагничивающих систем устройств производственных испытания постоянных магнитов (ПМ) [1, 4] не приспособлены для быстрой и точной установки ПМ в измерительную позицию. Этот недостаток устранен в намагничивающих системах прямоточного типа (НСПТ) [2, 3, 5]. Достоинством НСПТ является удобство загрузки и выгрузки образцов, поскольку движение последних происходит под действием собственного веса и магнитного поля по траектории, не имеющей отклонений от прямой линии.

Конструкция НСПТ для литых и порошковых ПМ, намагниченных вдоль продольной оси, приведена на рисунке 1. Она содержит намагничивающие катушки НК, магнитопровод М броневой конструкции, в полюсах которого находится сквозной канал с помещенной в него немагнитной направляющей Н. В центральной части направляющей находится блок первичных преобразователей индукции и напряженности ИК. Работает НСПТ следующим образом. Испытуемый ПМ поступает в направляющую и движется по ней под действием силы тяжести.

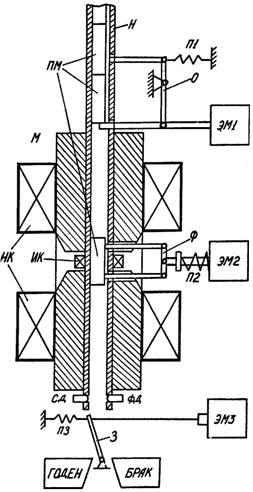
Рис. 1. Конструкция НСПТ

Одновременно в намагничивающие катушки подается ток, создающий в межполюсном пространстве НСПТ магнитное поле напряженностью, достаточной для фиксации ПМ в измерительной позиции (центр межполюсного пространства). После установки ПМ в измерительную позицию срабатывают механические фиксаторы Ф, удерживающие его в этом положении. Далее осуществляется перемагничивание ПМ по заданной программе под действием магнитного поля, создаваемого током в намагничивающих катушках. Электромагниты ЭМ1–ЭМ3 и пружины П1–П3 приводят в действие отсекатель О, фиксатор Ф и заслонку З соответственно.

Для оптимального проектирования НСПТ [6, 7, 10] необходима модель, описывающая процесс движения ПМ. Уравнение движения изделия в системе данного типа имеет вид:

(1)

где y - расстояние между центром изделия и центром межполюсного пространства; m - масса изделия; Р - сила тяжести изделия; Ft, Fn - тангенциальная и нормальная составляющие электромагнитной силы, действующей на изделие;  - коэффициент трения изделия о стенки направляющей; Bнс(H), Bи(Н) - магнитные характеристики материалов магнитопровода системы и изделия; G - обобщенный параметр геометрических размеров изделия и межполюсного пространства системы.

При решении уравнения (1) наибольшую сложность представляет определение тангенциальной Ft и нормальной Fn составляющих электромагнитной силы, действующей на испытуемое изделие. Использование метода конечных элементов (МКЭ) позволяет решить задачу расчета проекций Fx и Fy  вектора электромагнитной силы

При анализе различных вариантов НСПТ для определения сил, действующих на испытуемое изделие, использовались как расчетные методы теории поля, так и экспериментальные исследования. Измерение сил Fy и Fx  производилось на установке, принцип действия которой поясняет рисунок 2.

Рис. 2. Экспериментальная установка

Для измерения силы Fy выставляют заданные значения тока в катушках НСПТ и значения координаты y. Изменяя массу грузов, добиваются равновесия. Измерение силы Fx производится методом замещения. При заданных значениях тока и координаты y измеряют прогиб вставки. Затем такие же значения прогиба получают при помощи грузов на снятой из экспериментальной установки вставке. Координата y измеряется индикатором часового типа с ценой деления 0,01 мм; в качестве грузов используются наборы разновесов Г-4-1111.10; измерение деформации производится тензорезисторами типа 2ПКБ-20-200, измерительным преобразователем Ш74/2 и цифровым вольтметром В7-34А.

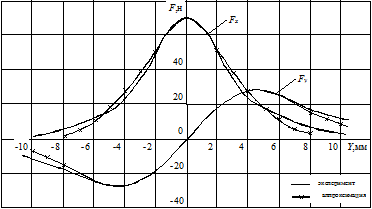
На основе анализа результатов исследований различных образцов систем данного типа предложено силы Fy и Fx аппроксимировать выражениями:

;              ,

где G1, G2, G3, аy, аx, n, q - коэффициенты, определяемые геометрическими размерами испытуемого изделия и межполюсного пространства системы.

Рис. 3. Результаты аппроксимации сил Fy, Fx

Погрешность аппроксимации составила 3% и 6% для Fy и Fx соответственно. Значения погрешности [8, 9] определялись по формуле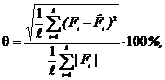

где - количество сопоставляемых точек;   - значения экспериментальной и расчетной сил в точке сопоставления i.

Моделирование ПМ произведено путем решения уравнения (1) с помощью пакета MATHLAB. Расчитано изменение координаты центра ПМ во времени. На рисунке 4 представлены траектория и фазовый портрет движения ПМ. Для ПМ массой 0,01 кг получено время движения в измерительную позицию – 0,45 с, точность позиционирования – 0,6 мм. При изменении массы ПМ от 0,0093 кг до 0,0107 кг время движения в измерительную позицию менялось от 0,39 с до 0,45 с, а точность позиционирования — от 0,51 мм до 0,43 мм.

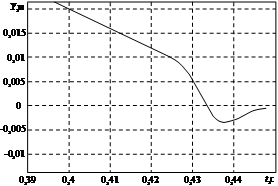
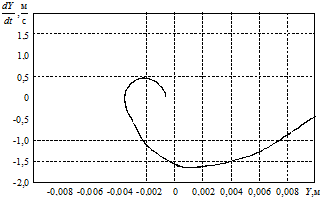
Рис. 4. Траектория и фазовый портрет движения ПМ

Используя понятие фазового пространства, уравнение (1) представим в виде:

,

(2)

где g - ускорение свободного падения; z = dy/dt.

Так как для правой части (2) не выполняются условия Коши, представим его в виде двух уравнений, для каждого из которых они выполняются:

,       .

На рисунке 5 изображен фазовый портрет движения ПМ. Движение устойчиво в малом, но неустойчиво в целом.

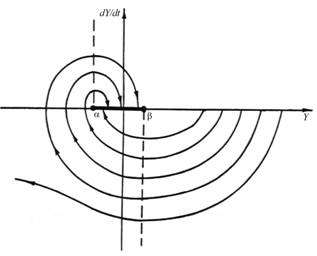
Рис. 5. Фазовый портрет движения ПМ

Координаты концов отрезка [a, b], определяющие предельные значения погрешности остановки ПМ, могут быть вычислены из уравнений:

            .

Решая их для области , получим:

,

.

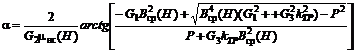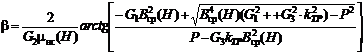В процессе движения ПМ получает энергию от сил электромагнитной природы и расходует ее на преодоление сил трения. В процессе движения энергия переходит из потенциальной формы в кинетическую и обратно. Энергетические процессы определяют характер движения ПМ. Запишем выражение для энергии ПМ, находящегося в точке с координатой y и обладающего скоростью z:

(3)

где           F+ - соответствует ; F- - соответствует .

Дифференцируя по времени выражение (3), получим:

.

(4)

С учетом (2) выражение (4) примет вид:

.

(5)

Последнее выражение показывает, что суммарная энергия образца постоянна на каждом участке фазовой траектории, для которого справедливо sign z = const.

Выделим из (3) потенциальную энергию:

Пусть движение образца начинается в момент времени t = 0, причем y(0) = y0 > 0, z(0) = 0, тогда с учетом выражения (5) имеем:

,

(6)

где   y1 = -y0 + c - первая точка пересечения фазовой траекторией движения ПМ оси OY при заданных начальных условиях; c - величина уменьшения радиуса фазовой траектории движения образца.

Преобразуем (6), используя разложение в ряд Тейлора и отбросив величины второй степени малости: .

Учитывая четность  и  и нечетность  и , из последнего выражения получим .

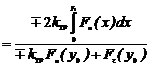Используя те же начальные условия, что и раньше, и с учетом (5) можно записать для энергии образца в точке с координатой y1:

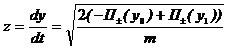 откуда

, а

Из последнего выражения определим время перехода от точки с координатой y0 в точку с координатой y1: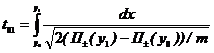

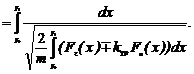
Обобщив полученный результат на p-ое пересечение фазовой траекторией оси OY, можно записать:

,      

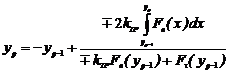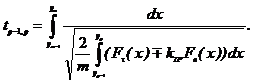
Использование этих выражений и условие остановки образца  позволяет без расчета фазовой траектории движения образца, при заданных начальных условиях рассчитать значение времени движения и погрешности установки ПМ.

Исследованы НСПТ, обеспечивающие автоматизацию процесса измерения и способные с высокой производительностью осуществлять транспортировку, ориентацию, фиксацию в измерительной позиции и перемагничивание испытуемых ПМ. Разработана математическая модель НСПТ, описывающая процесс движения ПМ. Предложены уравнения аппроксимации проекций вектора электромагнитной силы, действующей на ПМ в процессе движения его в измерительную позицию. НСПТ устройств испытаний ПМ обеспечивают суммарное время транспортировки, ориентации и фиксации магнита в измерительной позиции не более  450 мс при погрешности его установки в измерительную позицию не более 0,7 мм.

 

Статья подготовлена с использованием оборудования ЦКП «Диагностика и энергоэффективное электрооборудование» ЮРГПУ(НПИ).

Рецензенты:

Елсуков В.С, д.т.н., профессор кафедры «Автоматика и телемеханика», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова», г. Новочеркасск;

Гречихин В.В, д.т.н., профессор кафедры «Информационные и измерительные системы и технологии», ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) имени М.И. Платова», г. Новочеркасск.