Любая задача из области стационарных потоков может считаться задачей, находящейся в компетенции теории обобщенной проводимости (ТОП).
Действительно, с помощью формализации «одинаковые уравнения – одинаковые решения», частный результат исследования свойств смеси в каком-либо скалярном или векторном поле с успехом можно распространить на случай поля совершенно иной физической природы, если только качественно несхожие явления описываются одинаковыми по форме уравнениями.
Следовательно, самые первые (появившиеся в XIX в.) работы, посвященные исследованию свойств диэлектрических смесей, находящихся в электростатическом поле, правомерно считать пионерскими в области ТОП.
Как правило, истоки проблемы ТОП связывают с именами корифеев физики прошлого века – Пуассоном, Клаузиусом, Моссотти, Лорентцем [25, 42, 43, 44, 46, 47, 48], предложивших ряд формул и теорий определения диэлектрических и магнитных свойств смесей, ибо в силу исторически сложившихся обстоятельств первыми фундаментальными исследованиями по теории поля были исследования в области электрических и магнитных полей.
Однако, по-видимому, лишь Рэлей в 1892 г. впервые оценил общую природу проблемы, представляя результаты полученные им в области электростатики, применимые для других полей – тепловых, акустических и т.п. [39].
Интересно, что в обзоре Г.Н. Дульнева и Ю.П. Заричняка, приведенном в [7], первой работой в данном направлении ошибочно назван труд Максвелла «Treatise on Electri city and Magnetizing», который, как указали авторы обзора, публиковался в журнале “Phyl. Mag.” (5), 34, в 1892 г. В действительности же в 1892 г. в № 5 журнала”Phyl.Mag” была опубликована указанная нами работа Рэлея, а приведенное в [7] исследование Максвелла увидело свет в Оксфорде в 1904 г.).
Тем не менее, первым этапным трудом в ТОП следует, на наш взгляд, считать работу О. Винера [56], вышедшую в Лейпциге в 1912 г. Значение исследования О. Винера трудно переоценить хотя бы потому, что даже в настоящее время при проверке корректности вновь выведенных и (или) использующихся при расчетах свойств смесей формул прибегают к помощи теоретических постулатов О. Винера. После О. Винера первым из исследователей, подошедшим с системных позиций к проблеме ТОП, был немецкий физик К. Лихтенеккер, теоретические работы которого базировались на фундаментальных положениях О. Винера. К. Лихтенеккером получен ряд ценных результатов, широко использующихся в ТОП вообще и прикладных физических задачах в частности.
В 30-е и 40-е годы нашего столетия интерес к ТОП постепенно угас, и новые исследования получили толчок уже во второй половине ХХ века, видимо, в связи с реальными перспективами экономически эффективного использования композиционных материалов, изучение свойств которых как раз является предметом ТОП, или, как ее раньше называли, теории смесей. Весьма продуктивные общие правила анализа процессов переноса, сформированные К. Лихтенеккером, оказались забытыми, и на страницах научных журналов появились публикации, в которых заново «открывались» полученные ранее выводы. В [7] приведен как характерный пример в этом отношении выход в свет в 1965 г. объемного труда А. Миснара [12], автор которого получил результаты, совпадавшие с гораздо более ранними выводами К. Лихтенеккера.
К числу этапных работ в области ТОП, несомненно, принадлежит и статья В. Оделевского [13], опубликованная в 1951 г. Основаниями такого признания служат как ценность полученных автором результатов, так и то обстоятельство, что В. Оделевский подчеркнул всеобщий в рамках понятия термина «обобщенная проводимость» характер этих результатов и, пожалуй, впервые обосновал с позиций математической физики термин, впоследствии получивший столь широкое распространение.
Если подавляющее большинство названных выше работ посвящались вопросам исследования электрических и магнитных полей (в основном, разбирались задачи расчета диэлектрической проницаемости смесей), то в 60 – 70-х годах ХХ века широкое распространение получили работы в других областях, также давшие ценные результаты для общей теории обобщенной проводимости. Здесь в первую очередь следует отметить исследования Г.Н. Дульнева и его учеников в области теории теплопроводности, а также получившие широкое распространение в последние годы работы зарубежных и советских авторов по механике композитов.
Впрочем, вопросы применимости выводов ТОП к задачам механики композитов и установление соответствующих аналогий являются несколько специфичными и, как нам кажется, не получившими однозначного толкования. Учитывая последнее замечание, а также проведенный выше краткий исторический экскурс, обзор работ по ТОП будет произведен нами по следующим этапам:
- ранние теории (до выхода труда О. Винера [56], в котором впервые сформулированы фундаментальные положения теории смесей);
- теория смесей О. Винера;
- работы К. Лихтенеккера;
- теория изодиаметрических гетерогенных систем В. Оделевского;
- исследования структур с взаимопроникающими компонентами ( по Г.Н. Дульневу; Г.Н. Дульневу – Ю.П. Заричняку и др.)
- обзор теорий эффективных модулей в механике композиционных материалов.
«Довинеровские» теории
Первые важные результаты для ТОП были получены Пуассоном [47] при разработке теории магнетизма. Модель магнитного материала, предложенная и исследованная Пуассоном, представляла собой регулярную кубическую структуру, а именно, в вершинах кубов располагались изотропные магнитные ядра, разделенные непроводящим материалом. В более поздней работе [48] Пуассон предложил модель анизотропного магнитного тела, которая идентична вышеописанной, однако магнитные ядра представляли собой в данной модели не сферы, а трехосные эллипсоиды.
Мосотти [46] перенес теорию Пуассона из области магнетизма в область диэлектриков. Аналогичная модель была предложена Мосотти для аналитического определения взаимосвязи макроскопических параметров диэлектрика (диэлектрическая проницаемость ε, плотность ρ, молекулярная масса М) с микроскопическими (например, поляризуемость молекулы l, число молекул в единице вещества N и т.д.). Диэлектрик по Мосотти представляет собой неэлектропроводную материальную среду, в которой расположены электропроводные ядра-шары. Диаметр ядер мал по сравнению с размерами между центрами соседних ядер. Клаузиусом на модели Мосотти был получен ряд теоретических результатов [25], эквивалентных – с точки зрения ТОП – результатам Пуассона, а Лампа [38] попытался дать расширение модели Мосотти на случай неизотропных сред, предложив заменить проводящие шары-ядра на параллельно размещенные эллипсоиды. Правда, математическую модель такой среды Лампа не построил, однако ясно, что в принципе его модель не отличается от модели анизопропной магнитной среды по Пуассону.
Голландец Г.А. Лорентц и датчанин Л.Лоренц независимо друг от друга [42…44] предложили теорию смесей, состоящих из шариков в материальной среде, с помощью оптических представлений и получили результат, тождественный результату теории Клаузиуса-Мосотти, если заменить в формулах Клаузиуса-Мосотти диэлектрическую проницаемость на квадрат показателя преломления.
Знаменитое уравнение Клаузиуса-Мосотти для изотропного диэлектрика имеет вид:
![]() (1)
(1)
где: ![]() -
относительная диэлектрическая проницаемость;
-
относительная диэлектрическая проницаемость;
![]() – удельная поляризация диэлектрика (величина,
пропорциональная числу молекул в единице объема и поляризуемости молекулы).
– удельная поляризация диэлектрика (величина,
пропорциональная числу молекул в единице объема и поляризуемости молекулы).
Лоренц и Лорентц обобщили теорию Клаузиуса-Мосотти на
случай смеси ![]() - компонентов. Поскольку
общая поляризуемость смеси аддитивна удельным поляризуемостям с «весовыми»
коэффициентами, равными удельным объемам каждого из компонентов, формула
смешения Клаузиуса-Мосотти-Лорентуа-Лоренца имеет вид:
- компонентов. Поскольку
общая поляризуемость смеси аддитивна удельным поляризуемостям с «весовыми»
коэффициентами, равными удельным объемам каждого из компонентов, формула
смешения Клаузиуса-Мосотти-Лорентуа-Лоренца имеет вид:
![]() (2)
(2)
где: ![]() – относительная объемная концентрация i-го компонента в смеси;
– относительная объемная концентрация i-го компонента в смеси;
![]() – диэлектрическая проницаемость i-го компонента.
– диэлектрическая проницаемость i-го компонента.
Переходя к обобщенным проводимостям, получим самый известный «довинеровский» закон смешения:
![]() (3)
(3)
где: ![]() – эффективная ОП смеси;
– эффективная ОП смеси;
![]() – ОП i-го компонента.
– ОП i-го компонента.
Наряду с первыми доказательными соотношениями теории смесей – (2) и (3) – известна и простейшая формула смешения
![]() ,
,
получившая название формулы Ньютона-Зильберштейна для хаотической смеси. Конечно, эта формула представляет лишь чисто исторический интерес, т.к. ещё на заре развития теории смесей физики интуитивно чувствовали ограниченность использования в расчетах различных свойств смесей просто аддитивного закона.
Важным шагом на пути разработки теории смесей представляла собой теория Рэлея [50]. Модель Рэлея сходна с теми, которые рассматривали авторы соотношения (2): перпендикулярно силовым линиям поля в матрице расположены одинаковые цилиндры-включения. Отказавшись от идеализации о малости включений по сравнению с расстоянием между включениями, Рэлей получил строгое решение, базирующееся на введении специальных рядов с круговыми (плоская задача) или шаровыми (объемная задача) функциями. Однако последнее обстоятельство обусловило весьма частную применимость полученных автором (хотя и строгих с точки зрения математической физики) результатов: для случаев включений, форма которых отлична от шаровой или цилиндрической, результаты расчетов по модели Рэлея неприменимы.
Формула Рэлея для плоской задачи имеет вид [50].
![]() ,
(4)
,
(4)
где: ![]() – обобщенная проводимость смеси в направлении,
перпендикулярном осям параллельно ориентированных цилиндрических
включений;
– обобщенная проводимость смеси в направлении,
перпендикулярном осям параллельно ориентированных цилиндрических
включений;
![]() – относительная объемная концентрация включений в смеси;
– относительная объемная концентрация включений в смеси;
V=![]() ;
;
![]() – обобщенная проводимость включений;
– обобщенная проводимость включений;
![]() м
обобщенная проводимость субстанции, в которую введены включения (или, иначе,
матрицы);
м
обобщенная проводимость субстанции, в которую введены включения (или, иначе,
матрицы);
![]() ,
… – константы функций, введенных Рэлеем; так, С
,
… – константы функций, введенных Рэлеем; так, С![]() =0,30584; С
=0,30584; С![]() =0,013363
и т.д.
=0,013363
и т.д.
Дальнейшее развитие метод Рэлея получил в работе Хавелокка [27], который получил сходные результаты для случая параллельно-перекрестной пространственной сетки, в узлах которой размещались включения по типу рэлеевских. Позднее Рунге [52] распространил метод Рэлея на кубическую структуру с включениями в виде полных цилиндров.
Случай шарообразных включений, равномерно введенных в сплошную матрицу, рассмотрен в ряде работ. Результаты Максвелла, уточненные затем Вагнером, сводятся к следующей известной формуле, получившей название формулы Максвелла-Вагнера:
![]() ,
,
где обозначения ![]() и
и
![]() – те же, что и в формуле (4).
– те же, что и в формуле (4).
И все же из ранних работ по теории матричных смесей,
безусловно, следует особо выделить уже упоминавшуюся нами работу Рэлея [50].
Дело в том, что, помимо ряда частных соотношений, для конкретных структур,
автором этой работы были сделаны первые попытки исследований в направлениях,
послуживших предметом будущих обширных исследований. Здесь имеется в виду
исследование взаимопроникающих структур, детально развитое в работах второй
половины ХХ века (из которых прежде всего следует выделить , по нашему мнению,
работы Г.Н. Дульнева), а также частичное предвосхищение этапных в ТОП
результатов, полученных К. Лихтенеккером. Правда, оба этих аспекта исследования
Рэлей ограничил только весьма частным случаем ![]() (случай
так называемой «равноправной» смеси).
(случай
так называемой «равноправной» смеси).
Рэлей впервые ввел понятие «обращенная» ячейка исходной смеси, а также «условная» ячейка (рис. 1).
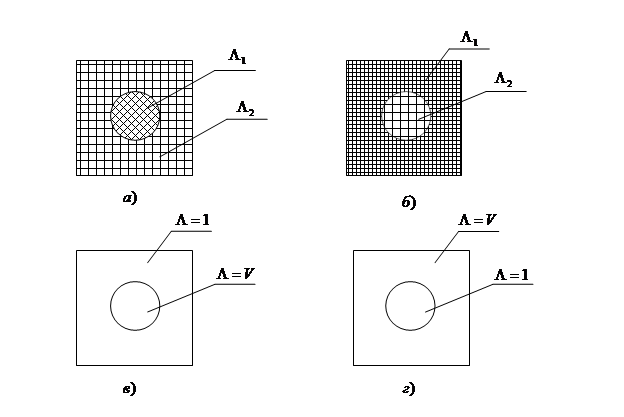
Рис. 1. Единичные ячейки рэлеевской модели:
а) прямая; б) обращенная; в) прямая условная; г) обращенная условная
Вместо прямой и обращенной ячеек типа а) и б)
соответственно, показанных на рис.1, Рэлей переходил к условным ячейкам типа в)
и г), а именно, вместо включений с ![]() ,
размещенных в матрице с
,
размещенных в матрице с ![]() ,
рассматривались ячейки с включениями, имеющими обобщенную проводимость
,
рассматривались ячейки с включениями, имеющими обобщенную проводимость ![]() , размещенными в среде с
, размещенными в среде с ![]() =1 (прямая задача), либо включения с
единичной обобщенной проводимостью в среде с
=1 (прямая задача), либо включения с
единичной обобщенной проводимостью в среде с ![]() (обращенная
задача). Заметим, что переходом к условной среде Рэлей предвосхитил также
первый постулат пропорциональности О. Винера; в дальнейшем такой прием часто
использовался исследователями (укажем, например, на работу В. Оделевского [13],
вышедшую в свет в 1951 г.).
(обращенная
задача). Заметим, что переходом к условной среде Рэлей предвосхитил также
первый постулат пропорциональности О. Винера; в дальнейшем такой прием часто
использовался исследователями (укажем, например, на работу В. Оделевского [13],
вышедшую в свет в 1951 г.).
При ![]() ячейки в)
и г), показанные на рис. 1, назовем равноправными. Определяем по формуле Рэлея
обобщенную проводимость
ячейки в)
и г), показанные на рис. 1, назовем равноправными. Определяем по формуле Рэлея
обобщенную проводимость ![]() обращенной
ячейки:
обращенной
ячейки:
![]() (5)
(5)
Рэлей доказал следующее соотношение:
![]() (6)
(6)
где: ![]() – ОП исходной ячейки;
– ОП исходной ячейки;
![]() – ОП обращенной ячейки.
– ОП обращенной ячейки.
Результат (6) означает, что при взаимной перестановке
включенного и окружающего материалов в случае равных относительных объемных
концентраций в результате рэлеевского метода расчета получаются 2 значения
эффективной обобщенной проводимости, среднее геометрическое которых ![]() в точности равно среднему
геометрическому исходных компонентов
в точности равно среднему
геометрическому исходных компонентов ![]() .
.
Несмотря на значимость ряда полученных результатов, Рэлей не дал должного обобщения, позволяющего выработать общие принципы решения задач теории обобщенной проводимости.
Таким образом, ранний период развития ТОП, который мы выше условно назвали «довинеровским» (отдавая дань этапному вкладу в теорию смесей О. Винера), характеризовался разработкой ряда соотношений для расчета структурно чувствительных свойств хаотических и регулярных матричных смесей, однако отсутствовал фундаментальный подход к проблеме, который бы устанавливал и обосновывал границы применимости полученных зависимостей и пути развития разработанных методов.
Теория смесей О. Винера
Если ранние исследователи (исключая, пожалуй, Рэлея) не уделяли должного внимания выделению общих положений из решения частных задач, т.е. всего того, что впоследствии будет названо ТОП, то О. Винер, пожалуй, даже чрезмерно абсолютизировал теорию смесей, как «…физически основную» [56].
Постановка Винером основной задачи ТОП, или, как было принято в литературе того времени, теории смесей, формулируется следующим образом. В поле стационарных токов (т.е. в поле электрическом, тепловом или иной физической природы) находится смесь с изотропным или анизотропным порядком компонентов. Учитывая, что свойства компонентов и структура смеси остаются неизменными, для волнового процесса, при котором длина волны велика по сравнению с характерными размерами составных частей структуры, требуется определить величину рассматриваемого свойства условного однородного тела, которым можно заменить смесь таким образом, что внешнее поле останется неизменным. Физические параметры такого условного однородного тела называют эффективными параметрами рассматриваемой смеси.
Предметом исследований Винера, в основном, являлась смесь в электрическом поле, и решение задачи заключалось в нахождении эффективной диэлектрической проницаемости смеси, однако Винер неоднократно подчеркивал применимость полученных результатов для других типов полей и других свойств, математическое описание которых аналогично рассматриваемому случаю. Поэтому правомерно считать О. Винера подлинным основателем теории смесей.
Еще до работ Винера многие исследователи сомневались в справедливости формулы (2) – «основного» по тем временам закона смешения, полученного Лоренцом и Лорентцем по аналогии с теориями Клаузиуса и Мосотти. Однако лишь Винер теоретически доказал противоречие формул типа (2) и (3) для хаотических структур смесей основным законам электростатистики. Обратив внимание на тот факт, что ход силовых линий электрического поля на границе раздела двух сред зависит не от абсолютных величин диэлектрических проницаемостей компонентов, а от их соотношения, Винер вывел следующее положение, которое мы сформулируем в общем виде для обобщенной проводимости (а не для диэлектрической проницаемости как одного из частных случаев):
Если обобщенные проводимости каждого из компонентов смесей изменить в т раз, во столько же раз изменится и обобщенная проводимость смеси
Это утверждение впоследствии получило в литературе название постулата пропорциональности, или I-го постулата Винера.
Легко
видеть, что формула Клаузиуса-Мосотти-Лоренца-Лорентца не удовлетворяет этому
постулату. Винер показал, что формула (2) достоверна лишь в случае малых
величин (![]() ), например, для случая
диэлектрической проницаемости газовых смесей.
), например, для случая
диэлектрической проницаемости газовых смесей.
Винер, как и ряд более ранних исследователей, также предпринял попытку «подправить» формулу Лоренц-Лорентца. Так, им была получена следующая формула, получившая название «винеровского закона смешения»:
![]() ,
(7)
,
(7)
где: ![]() – обобщенная проводимость смеси и i-го компонента соответственно;
– обобщенная проводимость смеси и i-го компонента соответственно;
![]() – винеровские параметры, величины которых
зависят от структуры исследуемой смеси.
– винеровские параметры, величины которых
зависят от структуры исследуемой смеси.
Формула
(7) отличается от (3) тем, что вместо постоянных коэффициентов 1 и 2
в числителе и знаменателе дробей соответственно фигурируют параметры ![]() и и.
и и.
Отметим, что еще Кеттелер [37], заменил лоренцовскую константу 2 параметром х, имея в виду следующее соотношение:
![]() , (8)
, (8)
однако у
Кеттелера х
рассматривается как некоторая эмпирическая константа в зависимости от материала
компонентов смеси. Учитывая, что Кеттелер не указал на зависимость параметра х
от структуры смеси, а также не дал никаких теоретических толкований этого
параметра, можно со всей определенностью констатировать, что уравнение (8) ни в
коей мере не может рассматриваться в качестве предшественника винеровского
закона смешения (7). Заслуга О. Винера как раз и заключается в том, что он указал в общем виде
на связь параметров ![]() и и со свойствами компонентов и
структурой смеси соответственно, а также привел в своих работах
конкретные значения этих параметров для ряда практически важных частных случаев
вида и ориентации смеси в основном поле.
и и со свойствами компонентов и
структурой смеси соответственно, а также привел в своих работах
конкретные значения этих параметров для ряда практически важных частных случаев
вида и ориентации смеси в основном поле.
Так,
Винер указал, что параметр ![]() выражается
через обобщенную проводимость матрицы, в которой размещены включения, т.е.
выражается
через обобщенную проводимость матрицы, в которой размещены включения, т.е.
![]() ,
,
а
параметр d
зависит от вида включений и ориентации последних в силовом поле. Например, для
круговых цилиндров, оси которых ориентированы перпендикулярно силовым линиям
поля, по Винеру ![]() , т.е. d=0,5, а для случая шаровых
включений
, т.е. d=0,5, а для случая шаровых
включений![]() , т.е. d=1 и т.д.
, т.е. d=1 и т.д.
Величина
и в винеровской формуле
возрастает с уменьшением угла между направлением вектора обобщенной сила и
границей раздела сред, т.е. с увеличением «параллельности» границы раздела сред
силовым линиям. Сам Винер называл параметр и «мерой расположения решетки»
включений в бинарной смеси [55]. Винер указал граничные значения параметров ![]() и и:
и и:
![]() для случая последовательного включения
компонентов (т.е. при ориентации границы раздела составных частей смеси
перпендикулярно вектору обобщенной силы), и
для случая последовательного включения
компонентов (т.е. при ориентации границы раздела составных частей смеси
перпендикулярно вектору обобщенной силы), и ![]() =
и=∞ для случая
последовательного включения компонентов(т.е. при параллельности границы раздела
силовым линиям поля). Кстати, Винер отметил, что параметры
=
и=∞ для случая
последовательного включения компонентов(т.е. при параллельности границы раздела
силовым линиям поля). Кстати, Винер отметил, что параметры ![]() и и
взаимосвязаны. По Винеру
и и
взаимосвязаны. По Винеру
![]() ,
,
где: f – так называемое число формы.
Например, для случая сферической формы одинаковых включений, достаточно удаленных друг от друга, f=2, Винер показал, как общие формулы для предельных случаев включения переходят в ранее выведенные им уравнения, описывающие слоистое и палочковое двойное преломление в бинарных матричных смесях с включениями в форме сфер и круговых цилиндров. В таблице 1 приведена сводка полученных Винером соотношений, где иллюстрируются основные результаты винеровских работ в области ТОП.
Таблица 1
Сводка формул обобщенной проводимости бинарных смесей,
полученных О. Винером
|
№ п/п |
Вид структуры смеси |
|
и |
Вид формулы смешения |
|
1. |
Произвольный, сферические включения |
|
|
|
|
2. |
Слои |
0 |
0 |
|
|
3. |
Круговой цилиндр
(1) в (2), |
|
|
|
|
4. |
Шары (1) в (2) |
|
2 |
|
|
5. |
Круговой цилиндр
(2) в (1), |
|
|
|
|
6. |
Шары (2) в (1) |
|
2 |
|
|
7. |
Слои или палочки |
|
|
|
Наконец, еще одним из наиболее важных результатов, полученных Винером, относятся так называемые неравенства Винера, а именно, постулат о том, что величина обобщенной проводимости смеси произвольной структуры всегда лежит в интервале значений для двух предельных случаев ориентации прямой границы раздела сред в силовом поле – перпендикулярно и параллельно силовым линиям поля:
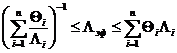 ,
(9)
,
(9)
Наряду с постулатом пропорциональности неравенства (9) –
важнейшее, не утратившее значение и в наши дни, наследие трудов Винера.
Практически для полной проработки основ ТОП теории смесей Винера не хватало
лишь вывода теоретических положений, которые позволяли бы находить значения
параметров ![]() и и в
общем винеровском законе смешения – формуле (7) – в зависимости от геометрии
структуры. Однако к решению подобных задач – правда, уже для законов смешения
иного вида – теоретически смогли подойти гораздо позже – уже в наши дни, т.е.
спустя более, чем полвека после опубликования основных результатов винеровской
теории смесей.
и и в
общем винеровском законе смешения – формуле (7) – в зависимости от геометрии
структуры. Однако к решению подобных задач – правда, уже для законов смешения
иного вида – теоретически смогли подойти гораздо позже – уже в наши дни, т.е.
спустя более, чем полвека после опубликования основных результатов винеровской
теории смесей.
Работы К. Лихтенеккера
К. Лихтенеккеру принадлежит большое число работ по теории обобщенной проводимости, значение которых также трудно переоценить. Во-первых, Лихтенеккер обобщил все известные до него результаты в области теории смесей – от ранних работ до О. Винера. Во-вторых, Лихтенеккер обработал большое количество экспериментальных данных по структурно-чувствительным свойствам смесей и сопоставил опытные данные с результатами расчетов по различным формулам смешения. И, наконец, Лихтенеккер предложил столь популярное и в наши дни для хаотических смесей логарифмическое правило смешения, а в соавторстве с К. Ротером – степенной закон смешения.
Отметим, что общий подход Лихтенеккера к проблемам ТОП в целом можно охарактеризовать как полуэмпирический; его разработки справедливо определены Г.Н. Дульневым и Ю.П. Заричняком [7] как «конструирование функций» смешения.
Логарифмический закон смешения был предложен Лихтенеккером
еще в своих ранних работах на основе примерно таких рассуждений. Предметом
исследования Лихтенеккера была так называемая «полностью равноправная»
взаимопроникающая структура, т.е. двухкомпонентная смесь с взаимопроникающими
компонентами при относительном объемном содержании их, равным ![]() . Предельные значения обобщенной
проводимости для такой смеси представляют собой среднее арифметическое и
среднее гармоническое из значений обобщенных проводимостей компонентов (правда,
термин «обобщенная проводимость» во времена Лихтенеккера не применялся, и в его
работах шла речь о расчете диэлектрической проницаемости «полностью
равноправной» бинарной смеси). Логика подсказывает, что для полностью
иррегулярной смеси значение обобщенной проводимости должно равняться некоторому
промежуточному значению относительно двух экстремумов.
. Предельные значения обобщенной
проводимости для такой смеси представляют собой среднее арифметическое и
среднее гармоническое из значений обобщенных проводимостей компонентов (правда,
термин «обобщенная проводимость» во времена Лихтенеккера не применялся, и в его
работах шла речь о расчете диэлектрической проницаемости «полностью
равноправной» бинарной смеси). Логика подсказывает, что для полностью
иррегулярной смеси значение обобщенной проводимости должно равняться некоторому
промежуточному значению относительно двух экстремумов.
Развивая свои ранние тезисы [39], а также догадку, высказанную Бенедиксом в практически не известной сегодня работе [22], Лихтенеккер просто предложил использовать для расчета ряда свойств «полностью равноправной» взаимопроникающей структуры правило среднего геометрического [40], т.к. известно, что среднее геометрическое двух чисел всегда является промежуточным значением между их средним гармоническим и средним арифметическим [9]. Лихтенеккер предложил свое правило для расчетов таких взаимно обратных свойств смеси, как электрическое сопротивление и электрическая проводимость. Самое любопытное заключалось в том, что результаты экспериментов хорошо описывались предложенным законом смешения. Далее Лихтенеккер обобщил свою методику на случаи с различной формой частиц компонентов в хаотической смеси и различного пространственного расположения частиц. Он показал также, что функция
![]() ,
,
или, что то же самое,
![]() , (10)
, (10)
где: а – некоторое выбранное основание логарифма(например, а=10 или а=е);
во всем диапазоне возможных значений ![]() и
и![]() (т.е.
от 0 до 1) удовлетворяет требованию давать промежуточные значения между средним
гармоническим и средним арифметическим значениями из
(т.е.
от 0 до 1) удовлетворяет требованию давать промежуточные значения между средним
гармоническим и средним арифметическим значениями из ![]() и
и ![]() .
Большое количество экспериментальных данных, полученных как Лихтенеккером, так
и рядом других исследователей, показали неплохое соответствие результатов опыта
расчетам по формуле (10), получившей название логарифмического закона смешения
или, иначе, уравнения Лихтенеккера.
.
Большое количество экспериментальных данных, полученных как Лихтенеккером, так
и рядом других исследователей, показали неплохое соответствие результатов опыта
расчетам по формуле (10), получившей название логарифмического закона смешения
или, иначе, уравнения Лихтенеккера.
Помимо логарифмического закона Лихтенеккер «сконструировал» и ряд других функций для описания структурно-чувствительных свойств хаотических физико-механических смесей.
При рассмотрении представительного объема двухкомпонентной смеси К. Лихтенеккер вводит меру вероятности, или относительную частоту и близости вида включения компонентов к случаю строго последовательного включения (когда линия раздела компонентов перпендикулярна силовым линиям поля). Под (1- и) понимается частота близости к случаю строго параллельного включения, когда линия раздела компонентов параллельна силовым линиям поля. Весь рассматриваемый объем смеси представляется в такой идеализированной модели состоящим из элементарных ячеек с параллельным и последовательным включением компонентов с относительным содержанием таких ячеек в смеси (1- и) и и соответственно. В качестве формул смешения для такой модели Лихтенеккер предложил функцию
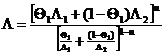 ,
(11)
,
(11)
Если считать, что ни один из типов включения не имеет преобладания в смеси, то надо считать и=0,5, и при этом соотношение (11) принимает вид
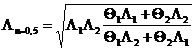 , (11,а)
, (11,а)
где: ![]()
Для случая «полностью равноправной» хаотической смеси, т.е.
при ![]() формулы (10) и (11) дают совпадающий
результат:
формулы (10) и (11) дают совпадающий
результат:
![]() .
(12)
.
(12)
Результатом более поздних теоретических изысканий Лихтенеккера стал выведенный им (в соавторстве с К. Ротером) степенной закон смешения [41]. Наряду с постулатом пропорциональности Винера авторами степенного закона смешения были описаны еще 3 постулата.
Первый постулат,
названный Лихтенеккером и Ротером постулатом «независимости от предыстории», в
принципе довольно очевиден, и он в ином, «неаксиоматическом», виде всегда
определяется практически во всех работах по ТОП. Говоря об отсутствии
химического взаимодействия компонентов и вторичных явлений в смеси, по существу
постулируют тот факт, что функция, описывающая свойство физико-механической
смеси одинаковых состава и структуры не зависит от способа получения смеси;
свойство смеси зависит лишь от свойств компонентов и от структуры смеси. При
этом, если не задана в явном виде функция границы раздела сред, а говорят о
полной хаотичности включения (т.е. разбирается случай полной иррегулярности),
функция F, описывающая свойство ![]() смеси, зависит от свойств
смеси, зависит от свойств ![]() и относительных объемных содержаний
и относительных объемных содержаний ![]() компонентов, т.е.
компонентов, т.е.
![]() .
.
Второй
постулат – неизменность применения формулы смешения
для смесей более высокого уровня. Это означает следующее. Пусть имеются две
смеси из одинаковых компонентов, но с различной концентрацией – ![]() и
и ![]() .
Теперь из этих двух смесей получают новую, так называемую смесь второго уровня;
причем, относительная объемная концентрация первой из смесей в смеси второго
уровня равна
.
Теперь из этих двух смесей получают новую, так называемую смесь второго уровня;
причем, относительная объемная концентрация первой из смесей в смеси второго
уровня равна ![]() . Согласно постулату независимости
от предыстории, обобщенные проводимости
. Согласно постулату независимости
от предыстории, обобщенные проводимости ![]() и
и
![]() смесей первого уровня выражаются
следующим образом (индексы при
смесей первого уровня выражаются
следующим образом (индексы при ![]() и
и ![]() опущены):
опущены):
![]() ,
,
![]() .
.
Математическая формулировка постулата неизменности формулы смешения для смеси более высокого уровня выглядит так:
![]() , (13)
, (13)
Из (13) следует также:
![]() ,
(14)
,
(14)
где: ![]() -
однородная функция от
-
однородная функция от ![]() и
и ![]() .
.
Наконец, третий постулат Лихтенеккера-Ротера, названный ими условием постоянства объемов, очевиден при совместном рассмотрении (13) и (14) и выражается как
![]() ,
(15)
,
(15)
Введем следующие сокращенные обозначения:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Из введенных выше постулатов следует, что функции F применимо тождество Эйлера:
![]() (16)
(16)
Согласно постулату неизменности формулы смешения для смеси более высокого уровня
![]() ,
(17)
,
(17)
а значит, с учетом (16) и введенных сокращенных обозначений, можем получить:
![]() ,
(18)
,
(18)
Дальнейший вывод уравнения Лихтенеккера-Ротера, или, иначе, степенного закона смешения основан на последовательных дифференцированиях функций, входящих в (18), а также интегрировании получающейся формулы.
Результатом указанных математических операций соотношение (18) приходит к следующему выражению
![]() , (19)
, (19)
называемому в литературе по ТОП степенным законом смешения Лихтенеккера-Ротера.
При k=0 интегрирование (19) дает логарифмический закон смешения – формула (10).
То, что логарифмический закон смешения является частным
случаем степенного при ![]() , видно из следующих
соображений. При показателе степени
, видно из следующих
соображений. При показателе степени ![]() вещественного
числа, гораздо меньшем 1, т.е.
вещественного
числа, гораздо меньшем 1, т.е. ![]() , до членов
высшего порядка выполняется соотношение:
, до членов
высшего порядка выполняется соотношение:
![]() , (а)
, (а)
В степенной закон
![]()
подставим соотношение (а). Получаем:
![]() .
.
Поскольку ![]() , из
последнего выражения тотчас следует логарифмическое правило смешения:
, из
последнего выражения тотчас следует логарифмическое правило смешения:
![]() .
.
К сожалению, как Винер для параметров и и ![]() , так и Лихтенеккер и Ротер не дали
указаний относительно вычислений значений k для
конкретных структур, отличных от случаев чисто последовательного, чисто
параллельного включений и полностью иррегулярной смеси. Другими словами,
наглядного толкования (интерпретации) показателя степени в степенном законе
смешения авторы закона не дали.
, так и Лихтенеккер и Ротер не дали
указаний относительно вычислений значений k для
конкретных структур, отличных от случаев чисто последовательного, чисто
параллельного включений и полностью иррегулярной смеси. Другими словами,
наглядного толкования (интерпретации) показателя степени в степенном законе
смешения авторы закона не дали.
К числу недостатков теорий Лихтенеккера ряд авторов работ по
ТОП [23] относит то обстоятельство, что формулы Лихтенеккера не выдерживают
предельных переходов, когда один из компонентов имеет значения ![]() , равные нулю или бесконечности (т.е.
, равные нулю или бесконечности (т.е. ![]() смеси при этом также становится
неопределенной, особенно это относится к случаю
смеси при этом также становится
неопределенной, особенно это относится к случаю ![]() ).
Нам думается, что при таких предельных переходах строго детерминированные
непрерывные функции вообще бессильны. Решение здесь, видимо, следует искать в
области статистических и дискретных методов, например, типа теории протекания [2]
или метода конечных элементов [15].
).
Нам думается, что при таких предельных переходах строго детерминированные
непрерывные функции вообще бессильны. Решение здесь, видимо, следует искать в
области статистических и дискретных методов, например, типа теории протекания [2]
или метода конечных элементов [15].
И все же, в заключение обзора работ К. Лихтенеккера, следует заметить, что значение общих правил ТОП и вообще разработок Лихтенеккера трудно переоценить. Характерным является тот факт, что при «новой волне» работ по ТОП, связанной с необходимостью разработки и исследования свойств новых композиционных материалов, ряд положений Лихтенеккера был как бы открыт заново (в [7] приведен конкретный пример по исследованию А. Миснара [12]).
Лихтенеккер был первым из исследователей, обратившим внимание на зависимость результатов расчета обобщенной проводимости смеси заданной структуры от способа разбиения ячейки – линиями параллельными или перпендикулярными вектору потока. Указанные выше способы разбиения ячейки структуры получили в работах Г.Н. Дульнева названия соответственно адиабатного и изотермического дробления ячейки (в работах Г.Н. Дульнева речь идет, в основном, о вопросах теплопроводности смесей с обобщением результатов для ТОП вообще; поэтому понятна такая терминология).
Для двухкомпонентной смеси с ячейкой плоскопараллельной
структуры типа «квадрат в квадрате» Лихтенеккер рассмотрел четыре случая: ![]() при двух возможных способах дробления
ячейки (значения обобщенной проводимости смеси, вычисленные при разбиении
ячейки линиями, параллельными и перпендикулярными вектору потока, Лихтенеккер
обозначает
при двух возможных способах дробления
ячейки (значения обобщенной проводимости смеси, вычисленные при разбиении
ячейки линиями, параллельными и перпендикулярными вектору потока, Лихтенеккер
обозначает ![]() и
и ![]() ) и
) и ![]() при
этих же двух способах дробления ячейки (для смеси соответственно получаются
при
этих же двух способах дробления ячейки (для смеси соответственно получаются ![]() и
и ![]() ).
).
Верхняя и нижняя границы значений обобщенной проводимости, по Лихтенеккеру, даются соотношениями:
![]()
![]() .
.
далее Лихтенеккер не стал на сторону «вилочного»
определения обобщенной проводимости, как это делали уже гораздо позднее при
исследованиях механических свойств композитов [44], а предположил, что
существует «истинное» значение ![]() смеси,
являющееся результатом усреднения последних соотношений:
смеси,
являющееся результатом усреднения последних соотношений:
![]() .
(20)
.
(20)
Любопытно, что формула (20) совпадает с формулами Дульнева и Дульнева-Заричняка для теплопроводности хаотических смесей [7]. Компенсация отличий, вызванных формой частиц, их положением и ориентацией относительно вектора потока тепла, как полагают Дульнев и Заричняк, может быть следствием многократного осреднения результатов при выводе соотношения (20).
Таким образом, исследования Лихтенеккера оставили, вероятно, один из наиболее заметных следов в ТОП.
Теория В.И. Оделевского
Результаты исследования гетерогенных систем изложены В.И. Оделевским в работе [13]. Однако по своей значимости эту единственную работу трудно переоценить, т.к. в подавляющем большинстве позднейших исследований (второй половины ХХ века) содержатся ссылки на ее результаты или сравнения с результатами расчетов по формулам, выведенным Оделевским.
Расчетные соотношения получены В.И. Оделевским путем решения электростатической задачи для матричных систем и статистических смесей с изодиаметрическими элементами, т. е. в предположении, что частицы, из которых состоят компоненты, приблизительно одинаковы по объему и форме.
Рассмотрим теорию В.И. Оделевского для матричных смесей.
Для случая малых концентраций в матричной системе,
образованной кубическими элементами (центры кубов образуют простую кубическую
решетку), Оделевский рассматривал вспомогательную систему II, в которой диэлектрические проницаемости компонентов по
сравнению с исходной системой I уменьшены в ![]() раз, где
раз, где ![]() -
диэлектрическая проницаемость матрицы. Таким образом, в системе II матричная фаза имеет условную диэлектрическую проницаемость
-
диэлектрическая проницаемость матрицы. Таким образом, в системе II матричная фаза имеет условную диэлектрическую проницаемость
![]() , а включения –
, а включения – ![]() , где
, где ![]() –
исходная диэлектрическая проницаемость включений. По уже известной нам теореме
пропорциональности (I постулат Винера, высказанный еще
раньше Рэлеем) диэлектрические проницаемости систем I и
II связаны соотношением
–
исходная диэлектрическая проницаемость включений. По уже известной нам теореме
пропорциональности (I постулат Винера, высказанный еще
раньше Рэлеем) диэлектрические проницаемости систем I и
II связаны соотношением
![]() (21)
(21)
При замене кубических включений эквивалентными
сферами, напряженность электрического поля ![]() внутри
сферы, поляризованной внешним однородным полем
внутри
сферы, поляризованной внешним однородным полем ![]() ,
определяется следующим образом [16]:
,
определяется следующим образом [16]:
![]() (22)
(22)
Взаимное влияние включений при небольших концентрациях
включений (![]() ) может быть учтено путем
аналогии с точечными индуцированными диполями. Поскольку в условной системе II включения расположены в среде с диэлектрической проницаемостью,
равной 1, правомерно учитывать лишь поляризацию включений. Для поляризующего
сферу (так называемого «внешнего») поля [13]:
) может быть учтено путем
аналогии с точечными индуцированными диполями. Поскольку в условной системе II включения расположены в среде с диэлектрической проницаемостью,
равной 1, правомерно учитывать лишь поляризацию включений. Для поляризующего
сферу (так называемого «внешнего») поля [13]:
![]() . (23)
. (23)
Под ![]() в (23)
понимается дипольный момент единицы объема в системе II:
в (23)
понимается дипольный момент единицы объема в системе II:
![]() .
(24)
.
(24)
Учитывая известное соотношение [16] между диэлектрической проницаемостью, и дипольным моментом единицы объема, находящегося в электрическом поле напряженностью Е:
![]() ,
,
из (24) получается:
![]() (25)
(25)
Решение (25) дает:
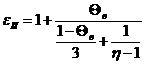 ,
,
откуда, с учетом (21), окончательно получается формула Оделевского:
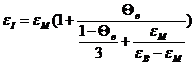 (26)
(26)
Для случая больших концентраций в матричной системе Оделевский использует решение токовой задачи обращенным методом сотов, приведенным в работе Е.В. Кувшинского. Суть этого метода заключается в следующем.
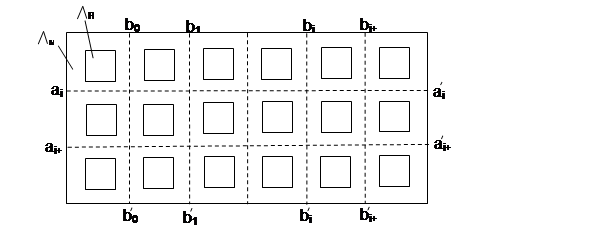 Рис. 2. Сечение матричной структуры
в виде кубической решетки [13]
Рис. 2. Сечение матричной структуры
в виде кубической решетки [13]
Рассмотрим металлическую матричную структуру,
показанную на рис. 2, где ![]() –
– ![]() – сечения эквивалентных поверхностей
плоскостью чертежа,
– сечения эквивалентных поверхностей
плоскостью чертежа, ![]() –
– ![]() – направление линий тока. Введем
тонкие непроводящие слои, образующие поверхность трубок тока, сечения которых
равны площади грани кубического включения. На рис. 3, а показан разряд
соответствующей элементарной ячейки и эквивалентная схема включения
проводимости.
– направление линий тока. Введем
тонкие непроводящие слои, образующие поверхность трубок тока, сечения которых
равны площади грани кубического включения. На рис. 3, а показан разряд
соответствующей элементарной ячейки и эквивалентная схема включения
проводимости.
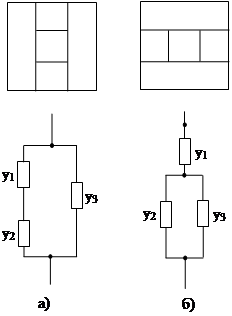 |
Рис. 3. Разрезы элементарных ячеек при сечении структуры, показанной на рис. 2, непроводящими (а) и сверхпроводящими (б) слоями [12]
При введении непроводящих слоев общая проводимость ![]() исходной системы, естественно,
снизится, т.е.
исходной системы, естественно,
снизится, т.е.
![]()
где: ![]() – проводимость системы с тонкими непроводящими
слоями.
– проводимость системы с тонкими непроводящими
слоями.
Предположим также, что вдоль эквипотенциальных
поверхностей (сечения ![]() на рис. 2) введены
весьма тонкие сверхпроводящие слои. Тогда (см. рис. 3,б) общая проводимость
системы должна возрасти, и теперь:
на рис. 2) введены
весьма тонкие сверхпроводящие слои. Тогда (см. рис. 3,б) общая проводимость
системы должна возрасти, и теперь:
![]() ,
,
где:
![]() – проводимость системы с тонкими
сверхпроводящими слоями.
– проводимость системы с тонкими
сверхпроводящими слоями.
В результате получается двойное неравенство:
![]() (27)
(27)
Смысл введения вспомогательных систем (рис. 3,а и рис.
3,б) заключается в том, что поле в них «кусочно – однородно», и потому возможен элементарный
расчет величин ![]() и
и ![]() .
.
Для системы рис. 3,а проводимость ![]() элементарной ячейки равна
элементарной ячейки равна
![]() (28)
(28)
где: ![]() =
=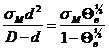 ;
;
![]() ;
;
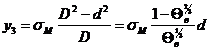 ;
;
![]() – удельная электрическая проводимость матрицы;
– удельная электрическая проводимость матрицы;
![]() – удельная электрическая проводимость
включений;
– удельная электрическая проводимость
включений;
D – расстояние между центрами кубических включений;
d – величина ребра кубического включения.
Для схемы рис. 3,б проводимость ![]() элементарной ячейки равна
элементарной ячейки равна
![]() ,
(29)
,
(29)
где: ![]() ,
, ![]() и
и ![]() – те же, что и в формуле (28).
– те же, что и в формуле (28).
После элементарных преобразований получается:
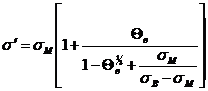 (30)
(30)
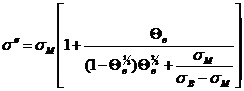 (31)
(31)
Сравнивая (30) и (31) между собой и с (26), можно
заключить, что решение для ![]() должно
иметь вид
должно
иметь вид
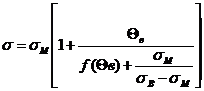 (32)
(32)
где: ![]() -
некоторая функция от относительной объемной концентрации включений.
-
некоторая функция от относительной объемной концентрации включений.
В соответствии с (27) функция ![]() должна удовлетворять следующему
неравенству:
должна удовлетворять следующему
неравенству:
![]() (33)
(33)
В области малых включений ![]() согласно
формуле (26):
согласно
формуле (26):
![]() (34)
(34)
В.И. Оделевский проверил, что это выражение годится
для случая больших концентраций ![]() .
.
Оделевский замечает также, что при ![]() функции
функции ![]() и
и
![]() имеют близкие значения, благодаря чему
требование соблюдения неравенства (27) является достаточно жестким. Отсюда
делается вывод, что функция
имеют близкие значения, благодаря чему
требование соблюдения неравенства (27) является достаточно жестким. Отсюда
делается вывод, что функция ![]() применима
во всей области возможных относительных объемных концентраций включений
применима
во всей области возможных относительных объемных концентраций включений ![]() , и поэтому для обобщенной проводимости
матричных смесей с кубическими включениями, центры которых образуют кубическую
решетку, а грани параллельны, справедлива формула:
, и поэтому для обобщенной проводимости
матричных смесей с кубическими включениями, центры которых образуют кубическую
решетку, а грани параллельны, справедлива формула:
 (35)
(35)
Помимо объемной задачи, подробное решение которой приведено выше, В.И. Оделевским получено также решение для случая плоской задачи, т.е. таких матричных структур, когда третья координата вследствие вытянутости включений может быть исключена из рассмотрения (например, включения в виде длинных параллельных призм или цилиндров).
Решение по вышеописанному методу Кувшинского для
случая больших концентраций в плоской задаче даст иной результат и для функции ![]() , а именно, для плоской задачи
, а именно, для плоской задачи
![]() (36)
(36)
Отличие (36) от (34) обуславливает и отличие общей формулы для обобщенной проводимости смесей матричной структуры в двухмерном случае. Для двухмерной задачи Оделевским получено соотношение:
 (37)
(37)
В (37) индекс «![]() »
указывает на принадлежность формулы для обобщенной проводимости
»
указывает на принадлежность формулы для обобщенной проводимости ![]() для случая вытянутых включений
(плоская задача).
для случая вытянутых включений
(плоская задача).
Отдельно рассмотрена В. Оделевским задача определения ОП статистической смеси.
Оделевский рассмотрел статистическую смесь с
невытянутыми изотропными включениями. Оделевский вводит вспомогательную систему
II с прежней геометрией, но с
диэлектрическими проницаемостями компонентов, уменьшенными в ![]() раз, где
раз, где ![]() -
диэлектрическая проницаемость исходной смеси, которая и подлежит определению. В
системе II диэлектрическая проницаемость i-го компонента равна
-
диэлектрическая проницаемость исходной смеси, которая и подлежит определению. В
системе II диэлектрическая проницаемость i-го компонента равна ![]() , где
, где ![]() -
истинная диэлектрическая проницаемость этого компонента. Вычисляя поляризацию
каждой частицы во вспомогательной системе II,
Оделевский полагает неизменным «внешнее» поляризующее поле напряженностью
-
истинная диэлектрическая проницаемость этого компонента. Вычисляя поляризацию
каждой частицы во вспомогательной системе II,
Оделевский полагает неизменным «внешнее» поляризующее поле напряженностью ![]() в системе. Полагая поле внутри частицы
равным полю внутри поляризованной сферы, для каждого из компонентов
индуцированный момент в единице объема системы II
равняется:
в системе. Полагая поле внутри частицы
равным полю внутри поляризованной сферы, для каждого из компонентов
индуцированный момент в единице объема системы II
равняется:
![]() ,
(38)
,
(38)
т.е. формально постулируется возможность наличия совокупности остальных частиц (кроме рассматриваемой i-й) в качестве непрерывной среды.
Так как
![]() ,
,
где индекс II указывает на вспомогательную систему II, то, с учетом (38)
![]() ,
,
что тождественно задаче Лорентца. Как видно, взаимодействие поляризованных частиц различных компонентов в выводе уравнения Оделевского для статической смеси не учитывается.
Согласно теореме пропорциональности во вспомогательной
системе II ![]() и
и ![]() .
Поэтому последнее уравнение дает
.
Поэтому последнее уравнение дает
![]() ,
(39)
,
(39)
или, переходя от электростатической аналогии к обобщенной проводимости,
![]() (40)
(40)
Метод введения вспомогательной системы заставляет оперировать с диэлектрическими проводимостями, меньшими 1, или, что то же самое, с отрицательными поляризуемостями. Формальным оправданием метода может служить применяемое в гравитационных расчетах введение отрицательных масс, т.е. такие представления – не более, чем удобный расчетный прием.
Для двухкомпонентных смесей из (40) получается громоздкое соотношение:
![]() (41)
(41)
где: ![]() .
.
Оделевским было проведено сопоставление результатов расчета по выведенным им формулам с результатами расчетов по другим известным формулам ТОП (Лорентца, Лихтенеккера, Вагнера), а также с экспериментальными данными. Из этого сопоставления [13] может быть сделан вывод о хорошем соответствии результатов теории В.И. Оделевского экспериментальным данным для смесей с сильно отличающимися по величине свойств компонентами, а также о лучшем совпадении теоретических и экспериментальных значений (по сравнению с другими формулами) во всей области концентраций компонентов в смеси при значительном различии (даже на несколько порядков) значений обобщенной проводимости компонентов.
Исследования Г.Н. Дульнева и Ю.П. Заричняка
Наиболее значимым в области ТОП в последнее время справедливо считать обобщения и новые результаты, описанные в работах Г.Н. Дульнева и Ю.П. Заричняка [7].
Дульнев и Заричняк классифицировали структуры несмешивающихся и химически не реагирующих компонентов по положениям границы раздела на 2 основные группы: структуры с вкраплениями (рис. 4,а) и структуры с взаимопроникающими компонентами (рис. 4,б). Своеобразный симбиоз двух основных типов структур, представленный на рис. 4,в,г, назван авторами классификации комбинированной структурой [7]. Само собой разумеется, что в пределах каждого из указанных типов структур может наблюдаться как хаотическое, так и упорядоченное включение компонентов.
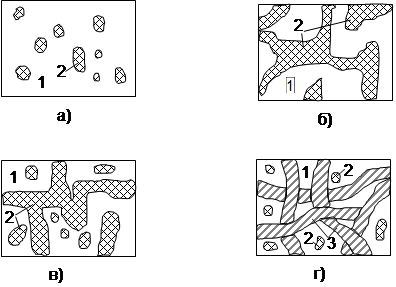 |
Рис. 4. Типы структур по Дульневу-Заричняку [7]
а) с вкраплениями 2 в матрице 1; б) с взаимопроникающими компонентами 1 и 2;
в) комбинированная двухкомпонентная; г) комбинированная трехкомпонентная
Характерной особенностью структур с вкраплениями является непрерывность связующего компонента (матрицы 1) в любом направлении и разрывное расположение вкраплений. В структуре с взаимопроникающими компонентами каждый из компонентов имеет непрерывную протяженность во всех направлениях.
Г.Н. Дульнев и Ю.П. Заричняк сформировали ряд очень
важных положений (названных ими правилами)
ТОП. Так, впервые в ТОП они указали, что упорядоченная структура может
рассматриваться как частный случай хаотической, а именно, ![]() систем с упорядоченной и хаотической
структурой равны друг другу, если структуры адекватны (в смысле принадлежности
к одинаковому типу модели – с вкраплениями, либо с взаимопроникающими
компонентами), а обобщенные проводимости и объемные концентрации компонентов
хаотической и упорядоченной структуры одинаковы.
систем с упорядоченной и хаотической
структурой равны друг другу, если структуры адекватны (в смысле принадлежности
к одинаковому типу модели – с вкраплениями, либо с взаимопроникающими
компонентами), а обобщенные проводимости и объемные концентрации компонентов
хаотической и упорядоченной структуры одинаковы.
Далее, вводя понятие элементарной ячейки как элемента
структуры, периодическое повторение которого в разных направлениях образует
систему с дальним порядком, Г.Н. Дульнев и Ю.П. Заричняк сформировали правило о том, что ![]() системы с дальним порядком равно
системы с дальним порядком равно ![]() элементарной ячейки этой системы. Это
правило вернее назвать теоремой (которую, естественно, можно доказать), однако
даже бездоказательное, интуитивное формулирование этой теоремы следует
признать важной вехой в развитии ТОП, т.к. практическая ценность содержащегося
утверждения несомненна: исследование и анализ сложного периодического
образования заменяется изучением простого единичного элемента – элементарной
ячейки структуры.
элементарной ячейки этой системы. Это
правило вернее назвать теоремой (которую, естественно, можно доказать), однако
даже бездоказательное, интуитивное формулирование этой теоремы следует
признать важной вехой в развитии ТОП, т.к. практическая ценность содержащегося
утверждения несомненна: исследование и анализ сложного периодического
образования заменяется изучением простого единичного элемента – элементарной
ячейки структуры.
Основное направление работ Г.Н. Дульнева и его учеников – прикладные задачи теплофизики: теплообмен в радиоэлектронной аппаратуре, теплопроводность сложных веществ и т.п. Однако Г.Н. Дульнев не замыкается в рамках теории теплопередачи и справедливо отражает значительно более широкое применение результатов своих исследований, развивая таким образом ТОП. Интересно, что и при решении тепловых задач авторы работы [7] постоянно используют метод электростатических аналогий, приводя исходную задачу к задаче расчета линейных электрических цепей.
При анализе сложных структур исследователи часто
используют дробление структуры, т. е. представляя исходную структуру
синтезированной из ряда простых. Этот прием позволяет дать аналитическое
описание свойств сложной структуры; решение находится из уравнений системы
определенным образом включенных в цепь проводимостей (или сопротивлений).
Пользуясь описанным широко распространенным приемом, Г.Н. Дульнев и Ю.П.
Заричняк, видимо, впервые (!) обратили внимание на зависимость конечного
решения основной задачи ТОП (т.е. определения величины эффективной обобщенной
проводимости смеси) от способа дробления структуры при анализе. В самом
деле, структуру, представленную двумя проекциями на рис. 5,а (куб в кубе),
можно условно разделить плоскостями А и Б на простые однородные составные части
по-разному: на рис. 5,б показано в двух проекциях дробление исходной структуры
плоскостями А и Б, параллельными вектору F поля обобщенных сил; на рис. 5,в
условные разделяющие плоскости А и Б перпендикулярны вектору ![]() (также показаны две проекции). Этим
различным способам дробления исходной двухкомпонентной структуры соответствуют
различные эквивалентные схемы включения в линейных электрических цепях, а
именно, для способа дробления структуры по рис. 5,б эквивалентная схема
представлена на рис. 6,а, а для способа дробления структуры по рис. 5,в – на
рис. 6,б.
(также показаны две проекции). Этим
различным способам дробления исходной двухкомпонентной структуры соответствуют
различные эквивалентные схемы включения в линейных электрических цепях, а
именно, для способа дробления структуры по рис. 5,б эквивалентная схема
представлена на рис. 6,а, а для способа дробления структуры по рис. 5,в – на
рис. 6,б.
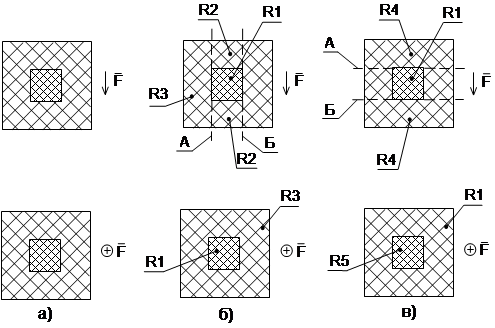 |
Рис. 5. Различные способы дробления структуры при анализе:
а) исходная структура; б) плоскости
дробления А и Б параллельны вектору ![]() поля
обобщенных сил; в) плоскости дробления А и Б перпендикулярны вектору
поля
обобщенных сил; в) плоскости дробления А и Б перпендикулярны вектору ![]() поля
поля
обобщенных сил
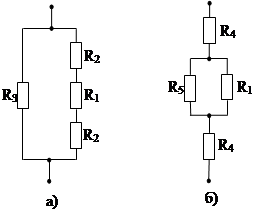
Рис. 6. Эквивалентные схемы включения сопротивлений в линейной электрической цепи при различных способах дробления исходной структуры:
а) дробление согласно рис. 5,б;б) дробление согласно рис. 5,в
Результат
расчета общего теплового сопротивления ![]() исходной
структуры зависит, таким образом, от способа разбиения, хотя разбиение – не
более чем абстрактный прием аналитического исследования. Для эквивалентных схем
рис. 6,а и рис. 6,б соответственно получается:
исходной
структуры зависит, таким образом, от способа разбиения, хотя разбиение – не
более чем абстрактный прием аналитического исследования. Для эквивалентных схем
рис. 6,а и рис. 6,б соответственно получается:
![]() ;
(42,а)
;
(42,а)
![]() ;
(42,б)
;
(42,б)
Принимая
во внимание, что тепловое сопротивление ![]() участка
однородной среды следующим образом выражается через геометрические размеры
участка
однородной среды следующим образом выражается через геометрические размеры ![]() и
и ![]() (
(![]() - длина пути теплового потока, т. е.
размер в направлении вектора теплового поля;
- длина пути теплового потока, т. е.
размер в направлении вектора теплового поля; ![]() -
площадь поперечного сечения рассматриваемого участка):
-
площадь поперечного сечения рассматриваемого участка):
![]() ,
,
где: ![]() - теплопроводность рассматриваемой
однородной среды,
- теплопроводность рассматриваемой
однородной среды,
из формул (42) можно получить выражения для эффективной теплопроводности рассматриваемой двухкомпонентной структуры типа «куб в кубе» в функции от теплопроводности исходных компонентов и концентрации компонентов в смеси.
Г.Н. Дульнев и Ю.П. Заричняк приходят к следующим формулам:
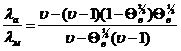 ;
(43,а)
;
(43,а)
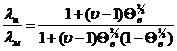 ;
(43,б)
;
(43,б)
где: ![]()
![]() – теплопроводность материала включения и
окружающей его матрицы соответственно;
– теплопроводность материала включения и
окружающей его матрицы соответственно;
![]() – относительная объемная концентрация включений
в рассматриваемой матричной структуре «куб в кубе».
– относительная объемная концентрация включений
в рассматриваемой матричной структуре «куб в кубе».
Индексы
«а» и «и» в формулах (42) и (43) при R и ![]() смеси
в целом указывают на различие способов дробления исходной структуры. Авторы
рассматриваемой теории назвали эти способы дробления соответственно адиабатными (рис. 5,б)
и изотермическими
(рис. 5,в) плоскостями. Видно, что при одинаковых значениях
смеси
в целом указывают на различие способов дробления исходной структуры. Авторы
рассматриваемой теории назвали эти способы дробления соответственно адиабатными (рис. 5,б)
и изотермическими
(рис. 5,в) плоскостями. Видно, что при одинаковых значениях ![]() и
и ![]() формулы
(43,а) и (43,б) дают различные результаты для расчетов эффективной
теплопроводности смеси.
формулы
(43,а) и (43,б) дают различные результаты для расчетов эффективной
теплопроводности смеси.
На наш
взгляд, условное обозначение эффективной обобщенной проводимости ![]() как
как ![]() («адиабатная»)
или
(«адиабатная»)
или ![]() («изотермическая») не совсем удачно, но
важно подчеркнуть, что Г.Н. Дульнев и Ю.П. Заричняк показали существенное
различие результатов расчета
(«изотермическая») не совсем удачно, но
важно подчеркнуть, что Г.Н. Дульнев и Ю.П. Заричняк показали существенное
различие результатов расчета ![]() от способа дробления структуры.
Понимая, что объективное свойство среды -
от способа дробления структуры.
Понимая, что объективное свойство среды - ![]() -
не должно зависеть от выбора условного метода подсчета величины значения в
рамках одних и тех же физических представлений, Г.Н. Дульнев и Ю.П. Заричняк
для определения
-
не должно зависеть от выбора условного метода подсчета величины значения в
рамках одних и тех же физических представлений, Г.Н. Дульнев и Ю.П. Заричняк
для определения ![]() предложили –
правда, без обоснования (!) –
следующую формулу:
предложили –
правда, без обоснования (!) –
следующую формулу:
![]() ,
(44)
,
(44)
где под ![]() и
и ![]() соответственно
понимается аналоги
соответственно
понимается аналоги ![]() и
и ![]() из формул (43,а) и (43,б).
из формул (43,а) и (43,б).
Проведя
ряд приближенных расчетов ![]() для
различных форм включений в кубической матрице, авторы рассматриваемой теории
сформулировали правило о том, что
форма невытянутых включений мало влияет на эффективную обобщенную проводимость
смеси. При этом, однако, авторы не привели данных по процентному различию результатов
расчетов
для
различных форм включений в кубической матрице, авторы рассматриваемой теории
сформулировали правило о том, что
форма невытянутых включений мало влияет на эффективную обобщенную проводимость
смеси. При этом, однако, авторы не привели данных по процентному различию результатов
расчетов ![]() для разных форм включений;
вообще же этот вывод, как и предыдущая формула (44), сформулированная в виде правила, представляются недостаточно
обоснованными в теории Г.Н. Дульнева и Ю.П. Заричняка.
для разных форм включений;
вообще же этот вывод, как и предыдущая формула (44), сформулированная в виде правила, представляются недостаточно
обоснованными в теории Г.Н. Дульнева и Ю.П. Заричняка.
Большой вклад внесли Г.Н. Дульнев и Ю.П. Заричняк в ТОП структур с взаимопроникающими компонентами; исследования таких структур выполнены ими весьма детально и всесторонне.
Базируясь
на упомянутом выше правиле о том,
что ![]() смеси в системе с дальним порядком
равна
смеси в системе с дальним порядком
равна ![]() элементарной ячейки, авторы
провели расчеты для
элементарной ячейки, авторы
провели расчеты для ![]() ячейки
двухкомпонентной смеси с взаимопроникающими компонентами. Восьмая часть ячейки,
показанная на рис. 7, идентифицируется с разнообразными элементарными ячейками
– как на рис. 8,а, так и на рис. 8,б – и, таким образом, может рассматриваться
как обобщающее представление структуры с взаимопроникающими компонентами.
ячейки
двухкомпонентной смеси с взаимопроникающими компонентами. Восьмая часть ячейки,
показанная на рис. 7, идентифицируется с разнообразными элементарными ячейками
– как на рис. 8,а, так и на рис. 8,б – и, таким образом, может рассматриваться
как обобщающее представление структуры с взаимопроникающими компонентами.
 |
Рис. 7. Восьмая часть элементарной ячейки структуры с взаимопроникающими компонентами
Для ![]() части ячейки (рис. 7) в работе [7]
дана формула связи относительной объемной концентрации
части ячейки (рис. 7) в работе [7]
дана формула связи относительной объемной концентрации ![]() с безразмерным параметром
с безразмерным параметром ![]() , где
, где ![]() -
ширина бруса упорядоченной решетки из материала с
-
ширина бруса упорядоченной решетки из материала с ![]() ,
L –
длина половины ребра куба элементарной ячейки (обозначения – см. на рис. 2.8).
Параметр С назван авторами
относительным размером бруса:
,
L –
длина половины ребра куба элементарной ячейки (обозначения – см. на рис. 2.8).
Параметр С назван авторами
относительным размером бруса:
![]() ,
, ![]() ,
(45)
,
(45)
причем,
при
![]() А=-1,
А=-1,
![]() ,
,
и
при ![]() А=1,
А=1,
![]() .
.
 |
|||
 |
|||
а) б)
Рис. 8. Различные виды элементарной ячейки модели с взаимопроникающими компонентами, восьмая часть которой имеет одно и то же представление, показанное на рис. 7
Обобщенная проводимость ![]() части ячейки при адиабатном дроблении
выражается выведенной Г.Н. Дульневым и Ю.П. Заричняком формулой:
части ячейки при адиабатном дроблении
выражается выведенной Г.Н. Дульневым и Ю.П. Заричняком формулой:
![]() , (46)
, (46)
где: ![]()
С – см. формулу (45).
Расчеты,
проведенные Дульневым-Заричняком, показали, что различие между ![]() и
и ![]() достигает
45% для случая
достигает
45% для случая ![]() и уменьшается
(примерно втрое) при
и уменьшается
(примерно втрое) при ![]() .
.
Пользуясь методикой построения эквивалентных электрических схем для расчета тепловых сопротивлений элементарных ячеек многокомпонентных смесей, Г.Н. Дульнев и Ю.П. Заричняк получили различные аналитические соотношения для определения эффективного значения обобщенной проводимости многокомпонентных систем с постоянным и переменным поперечным сечением компонентов.
Дульнев и Заричняк, исходя из выбранной ими методики расчета теплопроводности сложной структуры по схемам замещения тепловых сопротивлений электрическими, сформулировали еще одно важное правило для расчета обобщенной проводимости сложных смесей, а именно: любая многокомпонентная система может быть последовательно сведена к двухкомпонентной при расчете эффективной обобщенной проводимости.
Проведя
уточненные расчеты, учитывающие сопротивление линий тока в структуре с
взаимопроникающими компонентами, Дульнев и Заричняк получили следующую формулу
для ![]() :
:
![]() , (47)
, (47)
где: Ф – функция геометрии ячейки, определяющаяся из следующего приближенного соотношения:
![]() ,
,
![]() ,
,
![]() ,
,
С – параметр, связанный с
относительной объемной концентрацией ![]() второго
компонента следующим соотношением:
второго
компонента следующим соотношением:
![]() (48)
(48)
В
формуле (47) ![]() – обобщенная проводимость при так называемом
адиабатном дроблении элементарной ячейки условными плоскостями.
– обобщенная проводимость при так называемом
адиабатном дроблении элементарной ячейки условными плоскостями.
Для изотермического дробления Дульнев и Заричняк получили следующую зависимость:
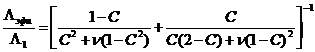 , (49)
, (49)
где: С – параметр, определенный соотношением (48).
Опять же
произвольно, без аргументированных
посылок, Дульнев и Заричняк предположили, что «точное» значение ![]() определяется как среднее арифметическое
из
определяется как среднее арифметическое
из ![]() и
и ![]() ,
т.е.
,
т.е.
![]() – см. аналогичную формулу (44).
– см. аналогичную формулу (44).
Г.Н. Дульневу и его ученикам (Заричняк, Тарновский) принадлежит, несомненно, наиболее весомый вклад в развитие ТОП в ее современном понимании.
Теории эффективных модулей в механике композиционных материалов
Исторически сложилось так, что различные исследователи, занимаясь теми или иными прикладными задачами, создавали различные теории определения эффективного значения какого-то определенного структурно-чувствительного параметра физико-механических смесей. Так, К. Лихтенеккер, О. Винер и более ранние исследователи, в основном, исследовали зависимость диэлектрической проницаемости смеси от параметров компонентов и геометрии структуры; Г.Н. Дульнев и его ученики, в основном, решали задачи по эффективной теплопроводности смесей и т.д. Как уже указывалось выше, только В.И. Оделевский и Г.Н. Дульнев сделали обобщение для различных случаев структурно-чувствительных свойств смесей, развив тем самым общую теорию, названную впоследствии теорией обобщенной проводимости (ТОП – согласно принятой нами аббревиатуре).
Так же «независимо» различными зарубежными и отечественными исследователями развивалась теория эффективных модулей композиционных материалов, являющаяся достаточно самостоятельным разделом механики композиционных материалов или, иначе, композитов. Неудивительно, что отсутствие общего подхода привело к повторению ряда результатов, уже известных в других теоретических дисциплинах (и этот факт еще раз говорит о значении создания общей теории – ТОП), хотя ряд довольно оригинальных методов и результатов, полученных в механике композитов, несомненно, заслуживает быть отмеченным в данном обзоре.
В основном, задачи определения эффективных модулей в механике композитов посвящены исследованиям модулей сдвига и упругости волокнистых, слоистых и других композиционных материалов, являющихся, согласно ранее данным определениям, физико-механическими смесями. Частным случаем таких смесей является исследование материалов с пустотами (порами), когда под включениями понимают материал с модулями, равными нулю или бесконечности.
Основной отличительной особенностью теории эффективных модулей в механике композитов от описанных выше теорий смесей является преимущественный отказ от попыток строго детерминированного определения единственного «эффективного» значения модулей композитов в пользу статистического определения «вилки» возможных допустимых значений параметра смеси в функции от параметров компонентов даже при известных или принятых в теоретических моделях геометрических соотношениях структуры или элементарной ячейки структуры. Это, безусловно, является важным шагом развития общей теории, и в дальнейшем будет использован именно такой «вилочный» подход. Важно лишь помнить о том, что теория будет иметь практическое применение и вообще практический смысл, если есть возможность на основе правдоподобных и непротиворечивых ограничений так «сузить» вилку допустимых (предсказываемых) значений эффективных модулей, чтобы предсказанные теоретически результаты могли стать основой будущих расчетов других параметров смеси с использованием эффективных модулей и – это главное! – достаточно надежно соответствовать опытным данным по исследованиям свойств смесей.
Отличные обзоры по общему состоянию проблемы теоретического определения эффективных модулей в механике гетерогенных смесей содержатся в работах М.Дж. Берана [3], Дж. Сендецки [15], Р. Кристенсена [11], Т.Д. Шермегора [21]; обзор работ, посвященных теории армированных полимеров, дан в работе В.В. Болотина [4].
Граничные
значения эффективных модулей многокопонентных композитов, полученные на основе
осреднения значений тензоров упругости и тензоров податливости (податливость –
параметр, обратный упругости, или, иначе, жесткости), получили соответственно
названия граничных значений по Фойхту ![]() [54]
и по Ройсу
[54]
и по Ройсу ![]() [51] – по фамилиям авторов
работ по такому осреднению значений тензоров упругости и податливости смеси.
[51] – по фамилиям авторов
работ по такому осреднению значений тензоров упругости и податливости смеси.
Выражения
![]() , (50)
, (50)
![]() ,
(51)
,
(51)
а также
![]() , (52)
, (52)
где: ![]() – относительные объемные концентрации
компонентов,
– относительные объемные концентрации
компонентов,
![]() – условное обозначение одного из модулей –
упругости (или Юнга) Е, объемного сжатия k , сдвига
– условное обозначение одного из модулей –
упругости (или Юнга) Е, объемного сжатия k , сдвига![]() ,
,
выражают предельные значения и вилку этих значений для обобщенной проводимости смесей и практически совпадают с неравенствами Винера – формула (9).
Из уже изложенного в предыдущих разделах материала понятно, что соотношения типа (52) имеют важное теоретическое значение, но, к сожалению, нулевое практическое. Поэтому все теоретические работы посвящены, в основном, «улучшению» пределов значений эффективных модулей (или, иначе, сужению вилки допустимых значений) в зависимости от геометрии структуры или каких-то других дополнительных данных о смеси.
Аналогом
допущений о значении эффективных модулей смеси, описанным выше при рассмотрении
работ Лихтенеккера – формула (20) – и Дульнева-Заричняка – формула (44) –
являются так называемое осреднение ![]() и
и ![]() смеси, предложенное впервые в механике
композитов Р. Хиллом [30]:
смеси, предложенное впервые в механике
композитов Р. Хиллом [30]:
![]() .
(2.60)
.
(2.60)
На самом же деле такое осреднение не следует считать каким-то прогрессивным шагом, ибо является, по сути, попыткой квазидетерминированного подхода к отысканию связи эффективного модуля смеси с модулями и концентрациями компонентов и отказом от «вилочного» подхода при нахождении допустимых граничных значений.
Для вычисления модулей Юнга смесей сложной структуры М. Такаянаги и С. Уэмура [53] предложили так называемый реологический подход, часто применявшийся в работах по ТОП Г.Н. Дульнева, когда строится схема замещения реального материала в виде сложной схемы последовательного и параллельного включения частиц компонентов. Результатом исследований Такаянаги-Уэмура стали следующие формулы:
![]() , (54,а)
, (54,а)
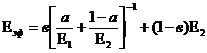 , (54,б)
, (54,б)
где: ![]()
![]() – относительное количество последовательно и
параллельно включенных элементов компонента 1,
– относительное количество последовательно и
параллельно включенных элементов компонента 1,
индексы 1 и 2 относятся к компонентам 1 и 2.
Понятно, что формулы типа (54) получают для вполне определенных схем включения элементов в общей схеме, и непонятно, как все же вычислять «а» и «в» для реальных структур. Поэтому ценность формул типа (54) также практически невысока.
Для случая малых концентраций включений в матрице существует ряд решений теоретической задачи об определении эффективных модулей двухкомпонентной смеси на основе так называемого вириального разложения матриц упругости С и податливости S, представляемых в виде [21]
![]() ;
;
![]() (55)
(55)
В (55) под ![]() понимается
меньшая из двух концентраций компонентов. Величины С и S представляют 6
понимается
меньшая из двух концентраций компонентов. Величины С и S представляют 6![]() 6 матрицы, компонентами которой
являются коэффициенты упругости
6 матрицы, компонентами которой
являются коэффициенты упругости ![]() и
податливости
и
податливости ![]() . Напряжение
. Напряжение ![]()
![]() и
деформации
и
деформации ![]() , согласно матричной схеме,
будут представлять собой векторы в шестимерном пространстве, т.е. их
компонентами будут
, согласно матричной схеме,
будут представлять собой векторы в шестимерном пространстве, т.е. их
компонентами будут ![]() и
и ![]() при i=1…6.
при i=1…6.
Поскольку при таком представлении трудно продвинуться дальше линейного приближения, этот метод расчета весьма ограничен и, как уже указывалось, применим практически лишь для задач о смесях с малой объемной концентрацией включений.
Одним из решений по методу вириального разложения являются приведенные в работе М.А. Кривоглаза и А.С. Черевко [10] соотношения:

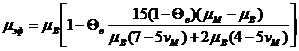 ,
(56)
,
(56)
где: ![]() и
и ![]() – объемный модуль и модуль сдвига
соответственно;
– объемный модуль и модуль сдвига
соответственно;
v – коэффициент Пуассона;
индексы «в» и «м» относятся к включению и матрице соответственно.
При линейном приближении вириального метода фактически принимается, что как в области вблизи включения, так и на достаточно больших удалениях от включения, постоянные упругости принимаются равными упругости матрицы. Дальнейшим уточнением модели являлось бы предположение о том, что на больших расстояниях от включения упругие свойства среды определяются эффективными модулями композита в целом. Такая модель получила название «самосогласованной», и результаты расчета по такой модели впервые были получены в работах А. Херши и Р. Хилла [29-33].
Для гранулированного композита Р. Хилл [31,32] получил следующее решение:
![]() ,
(57)
,
(57)
где: ![]() и
и
![]() – модули объемного сжатия по Фойхту и Ройссу
соответственно – см. формулы (50) и (51);
– модули объемного сжатия по Фойхту и Ройссу
соответственно – см. формулы (50) и (51);
![]() – модуль
сдвига, который в самосогласованной модели Хилла принят одинаковым как для
матрицы, так и для включения.
– модуль
сдвига, который в самосогласованной модели Хилла принят одинаковым как для
матрицы, так и для включения.
Из (57)
с учетом общеизвестных соотношений, связывающих модуль упругости Е, коэффициент
Пуассона v и модуль сдвига ![]() ,
получаются также следующие формулы:
,
получаются также следующие формулы:
![]() , (58)
, (58)
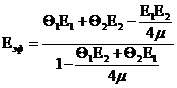 ,
(59)
,
(59)
Для слоистых композитов Р. Хилл [33] получил следующие зависимости для эффективных упругих постоянных композита:
![]() ,
(60)
,
(60)
![]() ,
(61)
,
(61)
![]() ,
(62)
,
(62)
![]() ,
(63)
,
(63)
где: ![]() – оценка по Ройссу (см. 51), т.е.
– оценка по Ройссу (см. 51), т.е.
![]() ;
;
индексы «![]() »
и «
»
и «![]() » относятся к модулям Юнга вдоль и
поперек слоев соответственно.
» относятся к модулям Юнга вдоль и
поперек слоев соответственно.
В дальнейшем Р. Хилл [29] и ряд других исследователей, о чем упоминает Дж. Сендецки [15], исследовали модель волокнистого композита на модели «цилиндр в цилиндре».
В работе Р. Хилла [34] для «самосогласованной» модели получены следующие выражения для эффективного модуля объемного сжатия, соответствующего дилатации в плоскости, перпендикулярной волокнам, а также модули сдвига поперек волокон и вдоль них.
Одной из самых значительных, можно сказать, этапных, работ по теоретическому определению вилки возможных значений эффективных модулей упругости и сдвига смесей, безусловно, следует считать работу Хашина и Штрикмана [28]. Практически все последующие работы ставили своей целью сравнивать вновь полученные расчетные формулы с вилкой Хашина-Штрикмана.
Граничные
значения для обобщенной проводимости ![]() двухкомпонентной
смеси по Хашину-Штрикману имеет вид:
двухкомпонентной
смеси по Хашину-Штрикману имеет вид:
![]() ,
(64)
,
(64)
![]() ,
(65)
,
(65)
![]() ,
(66)
,
(66)
где:
![]() и
и
![]() – минимальная и максимальная оценки
соответственно по методу Хашина-Штрикмана;
– минимальная и максимальная оценки
соответственно по методу Хашина-Штрикмана;
![]() .
.
Хашин и
Штрикман привели доказательство, что, если заданы лишь значения ![]() границы, даваемые формулами (64)…(66),
неулучшаемы [3]. Для «улучшения», т.е. сужения вилки (64), нужно задаться
дополнительными сведениями о геометрии структуры.
границы, даваемые формулами (64)…(66),
неулучшаемы [3]. Для «улучшения», т.е. сужения вилки (64), нужно задаться
дополнительными сведениями о геометрии структуры.
Рассматривая
соотношения Хашина-Штрикмана, представляется уместным сделать следующее
замечание. Если отвлечься от природы рассматриваемых явлений, легко заметить,
что формула (65) тождественна формуле Оделевского (35) для обобщенной
проводимости матричных смесей, если положить, что ![]() .
Если же
.
Если же ![]() , то вид формулы Оделевского
(35) совпадает с уравнением Хашина-Штрикмана (66). Знакомясь с результатами
исследований в какой-либо отрасли знаний, полезно постоянно сравнивать
формальный вид начальных и конечных соотношений с известными выводами из другой
области знаний. Мы постоянно проводим в данной работе эту мысль, которая
является, на наш взгляд, мощным аргументом в пользу развития ТОП на
аксиоматическом подходе, на феноменологической базе «одинаковые уравнения –
одинаковые решения».
, то вид формулы Оделевского
(35) совпадает с уравнением Хашина-Штрикмана (66). Знакомясь с результатами
исследований в какой-либо отрасли знаний, полезно постоянно сравнивать
формальный вид начальных и конечных соотношений с известными выводами из другой
области знаний. Мы постоянно проводим в данной работе эту мысль, которая
является, на наш взгляд, мощным аргументом в пользу развития ТОП на
аксиоматическом подходе, на феноменологической базе «одинаковые уравнения –
одинаковые решения».
М. Миллер [45], М. Беран [24] и другие исследователи получили на основе развития вариационного подхода, следующие соотношения:
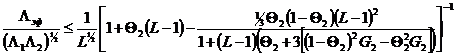 , (67,а)
, (67,а)
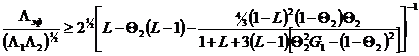 , (67,б)
, (67,б)
где:
![]() ,
т.е.
,
т.е. ![]() ,
,
![]() – числа, характеризующие форму ячеек включений
и матрицы.
– числа, характеризующие форму ячеек включений
и матрицы.
В
принципе ![]() могут быть вычислены как
определенные интегралы по формулам, данным М. Миллером [45]. В общем виде все
это громоздко и, если так можно выразиться, «ненаглядно». Миллер показал, что:
могут быть вычислены как
определенные интегралы по формулам, данным М. Миллером [45]. В общем виде все
это громоздко и, если так можно выразиться, «ненаглядно». Миллер показал, что:
![]() ,
(67,в)
,
(67,в)
и что ![]() соответствует
сферической форме включений,
соответствует
сферической форме включений, ![]() -
иглообразной форме,
-
иглообразной форме, ![]() форме диска. Если
форме диска. Если ![]() - объемная доля включений, то в
пределе
- объемная доля включений, то в
пределе ![]() при
при ![]() и при
и при ![]() границы
(67,а) и (67,б) совпадают.
границы
(67,а) и (67,б) совпадают.
Для простейшей модели двухфазного материала – симметричная
двухкомпонентная смесь (![]() ) рядом
исследователей [3] получено следующее соотношение:
) рядом
исследователей [3] получено следующее соотношение:
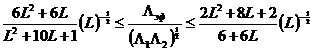 ,
(68)
,
(68)
Границы (68) лежат внутри интервала Хашина-Штрикмана и уменьшают его ширину примерно вдвое. Этот пример показывает, как уменьшается вилка Хашина-Штрикмана при учете дополнительной информации о структуре.
В работе
Г.Н. Савина и Л.П. Хорошуна [14] на основе методов теории случайных функций
получены обобщенные выражения для упругих постоянных стохастически армированных
материалов, которые при определенных значениях входящих в них величин сводятся
к рассмотренным выше соотношениям. Вводя в уравнения Дюамеля-Неймана,
связывающие напряжения, деформации и температуру компонентов, произвольные
постоянные ![]() и m вместо коэффициентов
и m вместо коэффициентов ![]()
![]() и
и![]() , Савин и Хорошун получили следующие
соотношения для объемного модуля
, Савин и Хорошун получили следующие
соотношения для объемного модуля ![]() , модуля
сдвига
, модуля
сдвига ![]() и коэффициента
температурного расширения
и коэффициента
температурного расширения ![]() двухкомпонентной
статической смеси:
двухкомпонентной
статической смеси:
![]() ,
(69,а)
,
(69,а)
![]() ,
(69,б)
,
(69,б)
![]() , (69,в)
, (69,в)
где: ![]() .
.
Из выражений (69,а) и (69,б) в предельных случаях получаются формулы Ройсса, Фойхта и Хашинв-Штрикмана.
Савин и
Хорошун показали также, что в случае ![]() ,
, ![]() формулы (69) тождественны решению на
основе уравнения совместности деформаций; в случае
формулы (69) тождественны решению на
основе уравнения совместности деформаций; в случае ![]() и
и
![]() формулы (69) тождественны решению на
основе уравнения совместности напряжений.
формулы (69) тождественны решению на
основе уравнения совместности напряжений.
При ![]() и
и ![]() из
(69,а) и (69,б) получится система уравнений для определения
из
(69,а) и (69,б) получится система уравнений для определения ![]() и
и ![]() ,
совпадающая с получаемой по методу «самосогласования».
,
совпадающая с получаемой по методу «самосогласования».
Учитывая
изложенное, можно считать уравнения (69) в некотором роде универсальными.
Однако не все ясно со значениями ![]() и т (и, конечно, п) в случае какой-либо дополнительной информации о структуре
регулярной смеси (а не просто стохастически армированной); вследствие этого
практическая ценность уравнений (69) не вполне ясна.
и т (и, конечно, п) в случае какой-либо дополнительной информации о структуре
регулярной смеси (а не просто стохастически армированной); вследствие этого
практическая ценность уравнений (69) не вполне ясна.
Во
многих теоретических работах рассматриваются упругие постоянные для некоторых
частных случаев соотношения концентраций компонентов и соотношений упругих
постоянных компонентов. Как отмечено в работах [21, 36], с практической (инженерной)
точки зрения все композиты могут быть условно разделены на три категории: 1)
композиции с высоким соотношением модулей включений и матрицы, т.е. ![]() ; этот случай включает в себя
большинство наполненных полимерных систем , причем, величина
; этот случай включает в себя
большинство наполненных полимерных систем , причем, величина ![]() может быть очень большой; 2)
композиции с малым отношением
может быть очень большой; 2)
композиции с малым отношением ![]() , например,
, например,
![]() <5; к таким композитам относятся
бетон и смеси металл-металл; 3) композиции с «мягким» включением, т.е.
<5; к таким композитам относятся
бетон и смеси металл-металл; 3) композиции с «мягким» включением, т.е. ![]() <1; предельным случаем являются
пористые материалы, когда
<1; предельным случаем являются
пористые материалы, когда ![]() =0.
=0.
Для ряда таких ограничений получены на основе приближенных методов расчета упругих постоянных достаточно наглядные и простые соотношения.
В работах [49, 26, 35] рассмотрена модель структуры в виде «куб в кубе». При нагружении такого композита нормальным однородным напряжением получена следующая приближенная формула [49]:
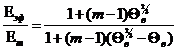 ,
(70)
,
(70)
где: т=![]() .
.
В случае пористой среды из (70) получается:
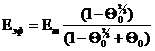 ,
(71)
,
(71)
где: ![]() – объемная концентрация пор.
– объемная концентрация пор.
В другом
предельном случае, полагая ![]() (идеально
жесткий наполнитель), из (71) получается:
(идеально
жесткий наполнитель), из (71) получается:
![]() .
(72)
.
(72)
Если на границе куба вместо однородного напряжения принять однородность нормального смещения, то вместо (70) получается [35]:
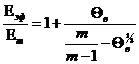 ,
(73)
,
(73)
откуда для пористой среды
![]() ,
(74)
,
(74)
а для жесткого наполнителя
![]() .
(75)
.
(75)
Как показали экспериментальные данные [21] , соотношение (70) дает лучшее приближение к эксперименту при т>>1, а при т<1 лучшее соответствие оказывается при расчетах по формуле (73).
В
работах Г.А. Ван Фо Фы [6] рассмотрен пористый материал с коэффициентом
Пуассона ![]() . При малой концентрации пор
получены следующие соотношения:
. При малой концентрации пор
получены следующие соотношения:
![]()
(76)
![]()
Из (76) для модуля Юнга получается:
![]() (77)
(77)
Как отмечено в [69], коэффициент концентрации напряжений для находящихся под растяжением пор, равен:
![]() .
.
Тогда (77) можно, с учетом v=0,2, представить следующим образом:
![]() (78)
(78)
При ![]() проведенная замена внесет определенную
погрешность, что для качественного анализа пористых материалов можно считать
допустимым.
проведенная замена внесет определенную
погрешность, что для качественного анализа пористых материалов можно считать
допустимым.
Говоря о
каких-либо допущениях, принимаемых при теоретических исследованиях модели,
нужно учитывать могущие возникнуть противоречия с известными теоретическими
результатами. Так, например, в работе [17] отмечено, что теория случайных
функций дает наилучшие результаты при вычислении упругих постоянных для больших
концентраций включений в текстурированных композитах (![]() ). Если же концентрация одного из
компонентов достаточно мала, то эффективные модули могут «выскочить» за вилку Хашина-Штрикмана.
). Если же концентрация одного из
компонентов достаточно мала, то эффективные модули могут «выскочить» за вилку Хашина-Штрикмана.
На хорошем уровне дано описание полученных А.Г. Фокиным и Т.Д. Шермегором результатов вычислений эффективных упругих модулей композитов в работе [20]. В этой работе приводятся результаты вычислений тензоров упругих модулей и податливостей с помощью перенормировки уравнений равновесия и несовместности. Во внимание приняты все многочастичные взаимодействия, однако расчет проведен в приближении учета только сингулярных частей производных функций Грина, что эквивалентно гипотезе однородности случайных составляющих полей напряжений и деформаций в пределах зерна.
Деформирование неоднородных твердых тел сопровождается возникновением в материале упругого поля, случайная составляющая которого, вообще говоря, обладает неоднородностью в пределах зерна. Это является причиной того, что связь между случайной и регулярной составляющими пока является нелокальной и описывается некоторой совокупностью интегральных операторов. Отмеченная нелокальность существенно усложняет проблему вычисления эффективных упругих постоянных и многоточечных моментных функций упругого поля. Лишь в некоторых частных случаях квазиоднородное деформирование приводит к однородности упругого поля в пределах зерна. Последнее имеет место для объемной составляющей упругого поля материала, в котором неоднородностью обладает лишь модуль всестороннего объемного сжатия К [18], а также для деформированных слоистых структур [19].
В работе
[20] с учетом всех многочастичных взаимодействий получены выражения для
определения эффективных модулей объемного сжатия К и сдвига ![]() ; при этом точные значения производных
функций Грина уравнений равновесия и несовместности заменены некоторыми
приближенными выражениями, что эквивалентно переходу от неоднородного в
пределах зерна упругого поля к однородному. Окончательно, используя принцип
согласования [1], А.Г. Фокин и Т.Д. Шермегор получили систему уравнений:
; при этом точные значения производных
функций Грина уравнений равновесия и несовместности заменены некоторыми
приближенными выражениями, что эквивалентно переходу от неоднородного в
пределах зерна упругого поля к однородному. Окончательно, используя принцип
согласования [1], А.Г. Фокин и Т.Д. Шермегор получили систему уравнений:
![]() ,
(79,а)
,
(79,а)
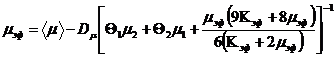 , (79,б)
, (79,б)
из которых
для конкретных случаев можно определить ![]() и
и
![]() (знак
(знак ![]() ,
как и ранее, означает усреднение по объему).
,
как и ранее, означает усреднение по объему).
Значения
![]() и
и ![]() ,
найденные из системы уравнений (79), всегда лежат внутри вилки допустимых
значений (52), а в ряде случаев – и внутри вилки Хашина-Штрикмана – см.
уравнение (64).
,
найденные из системы уравнений (79), всегда лежат внутри вилки допустимых
значений (52), а в ряде случаев – и внутри вилки Хашина-Штрикмана – см.
уравнение (64).
Для
случая ![]() решение системы уравнений (79)
дает:
решение системы уравнений (79)
дает:
![]() ,
,
что совпадает с формулой Лихтенеккера (12).
Из этого примера мы опять ясно видим связь уравнений ТОП с выведенными на совсем другой фундаментальной основе уравнений механики гетерогенных систем.
В работе [5] выведены формулы для ряда параметров гетерогенных смесей (коэффициента теплопроводности, коэффициента диффузии, коэффициента температурного расширения, упругих постоянных), а по сути – обобщенной проводимости, без принимаемого обычного ограничения о малости зоны микронеоднородностей. Предполагается, что локальные характеристики образуют непрерывное эргодическое однородное случайное поле. Конечные формулы получены для случая сильно изотропных поликристаллов. Авторы данной работы отметили большую сложность решения, а конечные результаты почти совпадают с методами борновского приближения (метод малого параметра) и по методу самосогласования. Естественно, решение лежит внутри границ Ройсса-Фойхта.
Попытка сужения вилки допустимых значений по Хашину-Штрикману сделана в работе Г.А.Ермакова, А.Г. Фокина и Т.Д. Шермегора [8]. Решение Ермакова-Фокина-Шермегора является дальнейшим развитием вариационного метода. В отличие от подхода Хашина-Штрикмана учтены дополнительные требования, которым должны удовлетворять виртуальные деформации при использовании приближения об однородном в фазе поле. Авторы цитируемой работы считают, что наложение этих требований обеспечивает решение в более узком диапазоне, чем даваемые уравнениями (64)…(66), полученными Хашином и Штрикманом. Границы вилки для допустимых значений эффективного модуля упругости рассмотрены на примерах п-компонентной смеси изотропных фаз (компонентов) и нетекстурированных поликристаллов кубической и гексагональной систем.
По Ермакову-Фокину-Шермегору:
![]() ,
(80)
,
(80)
где:
![]() ,
(81)
,
(81)
![]() ,
(82)
,
(82)
![]() – граничные значения вилки Хашина-Штрикмана,
выражающиеся соответственно уравнениями (65) и (66).
– граничные значения вилки Хашина-Штрикмана,
выражающиеся соответственно уравнениями (65) и (66).
Если учесть определения граничных значений по Фойхту и Ройссу – формулы (50) и (51) соответственно – то уравнения Ермакова-Фокина-Шермегора могут быть переписаны в виде:
![]() ,
(81,а)
,
(81,а)
![]() ,
(82,а)
,
(82,а)
где:
![]() и
и
![]() – граничные значения по Фойхту и Ройссу
соответственно.
– граничные значения по Фойхту и Ройссу
соответственно.
В громадном количестве работ, посвященных экспериментальным исследованиям по определению упругих постоянных композитов, полученные опытные данные сопоставляются с результатами теоретических исследований различных авторов. При этом, в первую очередь, общая корректность экспериментально полученных данных проверяется «попаданием» в вилку Ройсса-Фойхта (52). Далее устанавливается, лежат ли полученные значения в «вилке» Хашина-Штрикмана; затем сопоставляются данные эксперимента с какой-то известной (или предложенной) теоретической зависимостью и путем общего анализа (в основном, качественного), следует обоснование применимости к рассматриваемому конкретному случаю того или иного соотношения.
В целом можно отметить, что формальное совпадение соотношений для структурно чувствительных свойств смесей, полученных для различных параметров среды из различных отраслей прикладной науки, обуславливает правомерность и полезность существование самостоятельной общей теории – теории обобщенной проводимости.
Знакомясь с результатами создания теории того или иного структурно чувствительного свойства смесей в различных областях прикладной науки, можно заметить общую методологическую основу, заключающуюся в следующем. Сначала опираются на т.н. «фундаментальные соотношения» (например, классические уравнения электростатики – при исследовании диэлектрической проницаемости, или теплофизики – при исследовании теплопроводности смесей; классические тензорные уравнения для описания упругих свойств сплошной среды и т.д.), затем, в связи с невозможностью получения точных решений получающихся уравнений (вследствие недостаточности исходных данных), вводятся некоторые упрощения для получения аналитических решений, т.е. по сути от т.н. «классического подхода» остаются лишь исходные соотношения, теряющие свою «фундаментальность» по мере введения упрощающих положений. При этом в каждой из отраслей науки приходится учитывать свои специфические особенности.
Аксиоматическая ТОП
В противовес вышеуказанному подходу автором настоящего исследования была предложена аксиоматическая теория обобщенной проводимости (аксиоматическая ТОП), базирующаяся всего на двух исходных постулатах (аксиомах) – соотношениях типа (50) и (51) – формулах Фойхта и Ройсса соответственно, определяющих предельные ОП физико-механической смеси при ориентации границы раздела компонентов параллельно и перпендикулярно направлению вектора обобщенной силы соответственно. В каждой соответствующей области физики (электростатика, теплофизика, акустика, механика сплошных сред и т.д.) такие соотношения выводятся на основе общих уравнений в стационарных полях. Однако при построении общей ТОП эти соотношения постулируются. При этом оказывается возможным получение строгих математических решений при исследовании смесей сколь угодно сложной структуры. Более того, такой общий подход позволяет получить решение ряда задач, которые кажутся неразрешимыми без каких-либо дальнейших упрощений в той или иной области физики и её прикладных приложениях.
Общая методология построения аксиоматической ТОП изложена автором в работе [22].
На базе аксиом параллельного и последовательного соединения (имеющих вид соотношений по Фойхту и Ройссу соответственно) автором выведены соотношения для ОП двухкомпонентных смесей в функции от уравнения границы раздела сред.
Пусть единичная ячейка регулярной структуры двухкомпонентной
смеси размерами ![]()
![]()
![]() имеет
вид, показанный на рис. 9.
имеет
вид, показанный на рис. 9.
Рис. 9. К расчету ![]() смеси с
раздельным включением компонентов (плоская задача)
смеси с
раздельным включением компонентов (плоская задача)
Тогда значение ОП ![]() смеси (для
плоской задачи) лежит в следующем интервале:
смеси (для
плоской задачи) лежит в следующем интервале:
 , (83)
, (83)
где: ![]() ;
;
![]() ,
, ![]() – ОП компонентов условно названных «включение»
и «матрица» соответственно (см. рис. 9);
– ОП компонентов условно названных «включение»
и «матрица» соответственно (см. рис. 9);
![]() ,
, ![]() – размеры ячейки структуры;
– размеры ячейки структуры;
ось ![]() ориентирована
параллельно, а ось
ориентирована
параллельно, а ось ![]() – перпендикулярно направлению действия
обобщенной силы (вектор
– перпендикулярно направлению действия
обобщенной силы (вектор ![]() на рис. 9);
на рис. 9);
![]() ,
,![]() ,
,![]() ,
,![]() – уравнения границ раздела компонентов в осях
– уравнения границ раздела компонентов в осях ![]() и
и ![]() .
.
В случае объемной задачи уравнение (83) принимает следующий вид:
 (84)
(84)
где: ![]() ,
,![]() ,
,![]() ,
,![]() – уравнения плоскостей раздела компонентов в
объемной ячейке смеси регулярной структуры с раздельным включением компонентов.
– уравнения плоскостей раздела компонентов в
объемной ячейке смеси регулярной структуры с раздельным включением компонентов.
Для статистических смесей (смесей
иррегулярной структуры) автором аксиоматической ТОП предложен ряд моделей, из
которых можно отметить модель «представительного» объема, на основе которой
получаются расчетные соотношения для ОП смеси (![]() ), образующие еще более узкую «вилку»,
чем определяемая формулами Хашина- Штрикмана (64) … (66), а именно,
), образующие еще более узкую «вилку»,
чем определяемая формулами Хашина- Штрикмана (64) … (66), а именно,
![]() (85)
(85)
где: ![]() ,
,
![]() – ОП смеси по формулам (50) и (51)
соответственно, т.е. ОП смеси по Фойхту
– ОП смеси по формулам (50) и (51)
соответственно, т.е. ОП смеси по Фойхту ![]() и
ОП смеси по Ройссу ;
и
ОП смеси по Ройссу ;
![]() – относительная объемная концентрация одного из
компонентов, условно названного «включением» (для «матрицы», соответственно,
– относительная объемная концентрация одного из
компонентов, условно названного «включением» (для «матрицы», соответственно, ![]() ).
).
Значение общей теории обобщенной проводимости трудно переоценить в связи с широчайшим и повсеместным внедрением во все сферы человеческой деятельности композиционных материалов, являющихся, по сути, физико-механическими смесями различных компонентов.
Резюмируя, отметим, что теории обобщенной проводимости, зарождавшиеся и развивавшиеся в различных отраслях естественных наук (причем, иногда «параллельно» в различных отраслях прикладной науки), за почти полтора века (с момента появления первых работ по электростатике) прошли серьёзный путь от разрозненных исследований различных авторов до создания общей теории, применимой к самым различным физическим характеристикам сложных систем (смесей, композитов), обладающих свойством структурной чувствительности – диэлектрическая и магнитная проницаемость, теплопроводность, модули упругости, сдвига и т.п., ибо, по определению, ОП – это свойство смеси, определяемое не только концентрациями компонентов в смеси, но и ориентацией границ раздела компонентов смеси в соответствующем силовом поле.
Рецензенты:
Айрапетян В.С., д.т.н., доцент, профессор, заведующий кафедрой специальных устройств и технологий ФГБОУ ВПО «Сибирский государственный университет геосистем и технологий», г. Новосибирск;
Легкий В.Н., д.т.н, доцент, заведующий кафедрой автономных информационных и управляющих систем НГТУ, г .Новосибирск.
Библиографическая ссылка
Эдвабник В.Г. К ТЕОРИИ ОБОБЩЕННОЙ ПРОВОДИМОСТИ СМЕСЕЙ // Современные проблемы науки и образования. 2015. № 1-2. ;URL: https://science-education.ru/ru/article/view?id=19855 (дата обращения: 26.02.2026).



