В настоящее время разрабатываются проекты подводных судов для обеспечения эксплуатации месторождений углеводородов на шельфе арктических морей. Это обусловлено тем, что ледовая обстановка может меняться. При наступлении неблагоприятной ситуации судно может погрузиться под воду и продолжить снабжение буровой электроэнергией.
Следует отметить, что возможность погрузиться обусловлена добычей сырья на достаточной глубине.
Рассмотрим процессы моделирования взаимодействия судна со льдом при погружении. Заметим, что теоретическое решение этой задачи пока не получено из-за сложности физических процессов полного пролома ледяного покрова.
Классическая теория моделирования, разработанная Ю.А. Шиманским и Л.М. Ногидом, предъявляет к модели ледяного покрова следующие требования [4]:
![]() ;
; ![]() ;
; ![]() , (1)
, (1)
где ![]() - модуль геометрического подобия объекта взаимодействующего со льдом;
- модуль геометрического подобия объекта взаимодействующего со льдом;
h – толщина ледяного покрова;
![]() – предел прочности льда на изгиб;
– предел прочности льда на изгиб;
E – изгибный модуль упругости льда;
![]() – плотность льда;
– плотность льда;
![]() – коэффициент Пуассона льда.
– коэффициент Пуассона льда.
Индексами «н» и «м» обозначены натура и модель соответственно.
Модель ледяного покрова, полностью удовлетворяющая всем условиям моделирования, пока не найдена. Актуальным остается вопрос частичного подобия и связанного с ним метода пересчета результатов на натуру.
Для моделирования ледяного покрова используют модели искусственного льда, в которых прочность льда уменьшена таким образом, чтобы удовлетворить соотношению. Однако такое моделирование требует дорогостоящей технологии изготовления модельного льда и не позволяет полностью смоделировать все условия.
В НГТУ им. Р.Е. Алексеева на кафедре “Кораблестроения” был разработан метод моделирования в естественном льду, который обладает повышенной прочностью, чем требует строгая теория моделирования [4]. При моделировании обеспечивается равенство безразмерных прогибов, подобие параметров изгиба пластины на упругом основании, цилиндрической жесткости и напряженно-деформированного состояния льда. При этом картина разрушения льда в плане будет подобна, следовательно, одинаковыми будут число и расположение точек контакта объекта со льдом.
Отметим, что описанный метод моделирования не противопоставляется более строгому методу, основанному на подборе материала модели льда. Однако, он позволяет расширить объемы модельных исследовании, используя для них открытые бассейны и естественные водоемы, а также производить испытания крупномасштабных и полунатурных моделей.
Сразу следует заметить, что естественный лед обладает повышенной прочностью, чем требует строгая теория моделирования, поэтому широкое распространение получило мнение о невозможности его использования в качестве модели ледяного покрова.
Идея использования натурального льда состоит в попытке компенсации повышенной прочности меньшей толщиной [2].
Пересчет на натуру осуществляется по следующим зависимостям [1]:
![]() (2)
(2)
![]() , (3)
, (3)
![]() , (4)
, (4)
где ![]() – масштаб модулей упругости,
– масштаб модулей упругости,
![]() – геометрический масштаб,
– геометрический масштаб,
![]() – скорость деформирования натурного и модельного ледяного покрова,
– скорость деформирования натурного и модельного ледяного покрова,
![]() – проломная нагрузка для натурного и модельного льда.
– проломная нагрузка для натурного и модельного льда.
Справедливость изложенного метода моделирования проверялась на моделях речных ледоколов проекта Р-47 выполненных в масштабах 1:27, 1:18, 1:13,5 и проекта 1105 в масштабе 1:50, морского ледокола R – класса в масштабе 1:40 и некоторых других.
Испытания показали удовлетворительную сходимость с натурными данными.
Пересчет сопротивления для широкого диапазона масштабов моделей судов ![]() , а также для масштабной серии ледокола проекта Р-47 не выявили, сколько-нибудь заметного масштабного эффекта.
, а также для масштабной серии ледокола проекта Р-47 не выявили, сколько-нибудь заметного масштабного эффекта.
Были проведены исследования погружения вмороженных в лед серии унифицированных моделей с целью определения влияния отношения длины судна к ширине ![]() , площади ватерлинии, солености льда, угла наклона борта к ватерлинии на способность судна погружаться. По результатам испытаний были получены зависимости, с помощью которых могут быть получены данные по проломному усилию для судов с характеристиками, отличными от моделей и для новых ледовых условий. Методика пересчета испытаний моделей объекта с систематически изменяемыми характеристиками базируется на теории моделирования деформирования и разрушения ледяного покрова.
, площади ватерлинии, солености льда, угла наклона борта к ватерлинии на способность судна погружаться. По результатам испытаний были получены зависимости, с помощью которых могут быть получены данные по проломному усилию для судов с характеристиками, отличными от моделей и для новых ледовых условий. Методика пересчета испытаний моделей объекта с систематически изменяемыми характеристиками базируется на теории моделирования деформирования и разрушения ледяного покрова.
Схематизированные модели подводных судов были выполнены из стальных труб диаметром Æ168 мм толщиной t=4 мм и разных длин l1=500 мм; l2=750 мм; l3=1000 мм; l4=1500 мм с возможностью уточнения масштаба моделей в ходе проектирования натуры. С торцов трубы закрывались водонепроницаемыми заглушками, а внутри заполнялись вспенивающимся пенопластом. Сверху на трубах устанавливались площадки для крепления моделей к динамометру и ручки для переноса модели. Схемы моделей приведены на рис. 1 и 2. Модели закреплялись к штоку пресса и вмораживались в лед при разной осадке, что соответствовало форме борта близкой к вертикальной а) и наклонной б), в) и соответственно запасу плавучести для этих случаев 20%, 35%,50%.
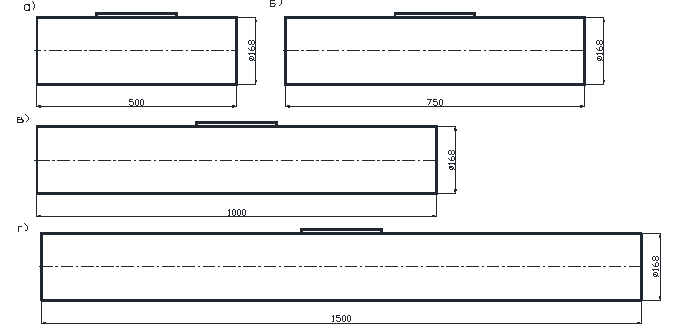
Рис 1. Схемы моделей подводного судна
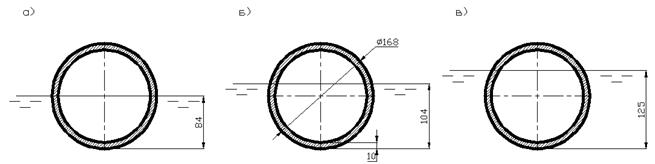
Рис 2. Схема вмораживания моделей в лед
Модельные испытания проводились в специальном ледовом опытовом стенде, расположенном на открытом воздухе. Более полное описание стенда дано в [5].
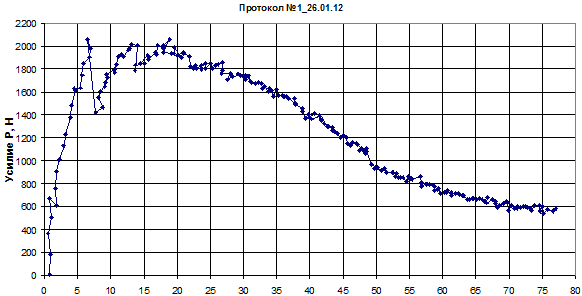
Испытания проводились в пресном льду естественного состава при отрицательных температурах воздуха. Ледовый бассейн заполнялся пресной водой, под пресс устанавливалась модель судна, закреплялась к штоку пресса и оставалась в воде (для заданной осадки) при намораживании льда требуемой толщины. Пример диаграммы разрушения показан на рис. 3.
Прогиб льда w, мм
Рис. 3. Пролом льда 26.01.12 г.
Длина модели в эксперименте на рис.3 L=750мм, осадка T=84мм, толщина льда h=28мм.
Испытания проводились для толщин модели льда ~10 мм, ~20 мм, ~30 мм, ~40 мм.
Для аппроксимации проломного усилия предложена формула [2]
![]() (5)
(5)
где![]() – коэффициент удельной энергии разрушения льда при погружении вмерзшего подводного судна, кПа;.
– коэффициент удельной энергии разрушения льда при погружении вмерзшего подводного судна, кПа;.
![]() – коэффициент, учитывающий влияние отношения длины нагрузки к ширине нагрузки.
– коэффициент, учитывающий влияние отношения длины нагрузки к ширине нагрузки.
![]() – коэффициент, учитывающий влияние площади нагрузки.
– коэффициент, учитывающий влияние площади нагрузки.
![]() – средняя прочность льда на изгиб в условиях опыта,
– средняя прочность льда на изгиб в условиях опыта, ![]() МПа.
МПа.
![]() – параметр упругого основания при изгибе ледяной пластины,
– параметр упругого основания при изгибе ледяной пластины,
Е – модуль упругости льда, принято Е=5×106МПа,
m – коэффициент Пуассона для льда, m=0,36,
r – плотность воды, , r=1,000 т/м3
g – ускорение свободного падения, g=9,81м/с2.
Полученные данные при определении влияния L/B и площади объекта использовались для определения проломной нагрузки подводного судна.
Планирование эксперимента в полном объеме затруднено. Это связано с неизбежной случайностью толщины ледяного поля в момент проведения испытания. Прогноз толщины намораживаемого льда базируется на времени и температуре воздуха. Но случайные метеорологические факторы (влажность, давление, динамика температуры, ветер) вносят свой вклад в фактическую толщину модели ледяного покрова, которая определяется сразу после разрушения ледяной пластины.
Соотношения геометрических параметров моделей имеют необходимый диапазон изменчивости, но конкретные соотношения параметров проектируемого объекта могут не совпадать с дискретным рядом моделей. Поэтому экспериментальные данные сначала подвергаются предварительной обработке. Строятся диаграммы в координатах сила – прогиб. Численные характеристики диаграмм аппроксимированы полуэмпирическими зависимостями, учитывающими существенные факторы процесса деформирования и разрушения льда. Например, проломное усилие описывается уравнениями вида (5). Затем рассчитываются кривые для моделей с параметрами вариантов натуры. Затем в заданном диапазоне проектируемого объекта, заданных его характеристиках выполняется пересчет данных на натуру.
Пересчет толщины ледяного покрова и проломного усилия выполняется по формулам (2) и (3). Физико-механические характеристики льда при пересчете берутся для модели и натуры соответственно. Для учета влияния ледовых условий на облик и конструктивные особенности подводного судна используется формула расчета проломного усилия, полученная на основе анализа ледовых испытаний (3).
Уравнение (5) показывает, что к снижению проломной нагрузки или к увеличению толщины проламываемого ледяного покрова при погружении приводит уменьшение площади ватерлинии надводного положения, а также уменьшение отношения длины к ширине L/B. Эта формула описывает экспериментальные данные. Для пересчета на натуру необходимо определить масштаб пересчета по длине натуры и модели и воспользоваться формулами (2) и (3).
Получены нижние пределы толщин проламываемого льда. Это связано с тем, что методы пересчета не в полной мере адекватно отражают современное состояние вопроса.
Для конкретного проекта подводного судна должны быть разработаны таблицы и графики, позволяющие принимать эксплуатационные решения о необходимости погружения при вмерзании в лед. Необходимо контролировать соленость воды, температуру воздуха и толщину ледяного покрова.
При моделировании взаимодействия судна с ледяным полем при погружении встает вопрос о моделировании силы адгезии льда к металлу корпуса судна. Адгезия зависит [1,3] от солености льда, материала корпуса, характера взаимодействия и других факторов.
При испытаниях моделей в ледовых условиях адгезию трудно смоделировать и пересчитать на натурные условия, поэтому важно установить разрушается ли ледяной покров от изгибных напряжений или же (если адгезия мала) просто соскальзывает вниз вдоль кромки льда. Поэтому, важно определить степень ее влияния на процесс моделирования погружения натурного судна.
Сила адгезии натурного и модельного судна можно определить по формулам
![]() (6)
(6)
![]() (7)
(7)
где ![]() – напряжение сцепления материала со льдом,
– напряжение сцепления материала со льдом,
![]() – периметр натурного судна и модели по действующую ватерлинию.
– периметр натурного судна и модели по действующую ватерлинию.
При моделировании погружения в естественном льду используется лед уменьшенной толщины, чем это требуется по классической теории моделирования.
Подставляя формулу (2) в (6) и (7) получим:
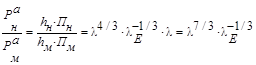 (8)
(8)
Проведенные в бассейне измерения модуля деформации ![]() тонкого пресноводного льда и сопоставления с натурными данными, указывают на его зависимость от толщины льда [1]. Эту зависимость в широком диапазоне можно аппроксимировать формулой
тонкого пресноводного льда и сопоставления с натурными данными, указывают на его зависимость от толщины льда [1]. Эту зависимость в широком диапазоне можно аппроксимировать формулой
![]() (9)
(9)
где ![]() – коэффициент пропорциональности.
– коэффициент пропорциональности.
Поэтому будем полагать, что масштаб ![]() при испытании в естественном льду равен [3]
при испытании в естественном льду равен [3]
![]() (10)
(10)
Подставляя (10) в (8) получим
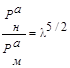 (11)
(11)
Из формулы (11) видно, что пересчет модельных результатов производится по масштабу в меньшей степени, чем при пересчете разрушения от изгиба. Однако, как показали результаты эксперимента по пролому вмороженной в лед пластины, усилия смерзания кратно превышают усилия ломки ледяного покрова изгибом. Адгезия стали корпуса со льдом настолько велика, что в любом случае удерживающие от погружения подводного судна усилия определяются проломной нагрузкой ледяного покрова.
Так, по результатам пересчета экспериментальных данных на натуру, величина проломной нагрузки для ледяного покрова толщиной 1,0м для судна длиной 82м и шириной 13м равна 6012кН. Сила адгезии того же судна при касательных напряжениях 0,5МПа [1], составляет 95000кН.
Ряд опытов [1] показывает, что соленость воды более 15‰ практически не влияет на величину адгезии, а при меньшей солености увеличивает ее. При солености 20-30‰ можно считать адгезию постоянной, но в модельных опытах в пресноводном льду, эта величина будет выше.
В результате можно сделать выводы:
- полностью выполнить все условия моделирования не удается. Производится моделирование по частичным критериям.
- разрушение при погружении энергомодуля происходит от изгиба, моделированием адгезии можно пренебречь.
- уменьшение площади ватерлинии надводного положения, а также уменьшение отношения длины к ширине L/B приводит к уменьшению проломной нагрузки.
- метод моделирования в естественном льду позволяет расширить объемы модельных исследований, используя для них открытые бассейны и естественные водоемы, а также производить испытания крупномасштабных и полунатурных моделей.
Рецензенты:
Химич В.Л., д.т.н., профессор, заведующий кафедры «Энергетические установки и тепловые двигатели» НГТУ им. Р.Е. Алексеева, г. Нижний Новгород;
Захаров Л.А. д.т.н., профессор кафедры «Энергетические установки и тепловые двигатели» НГТУ им. Р.Е. Алексеева, г. Нижний Новгород.
Библиографическая ссылка
Грамузов Е.М., Зуев В.А., Ларин А.Г. МОДЕЛИРОВАНИЕ ВЗАИМОДЕЙСТВИЯ ПОДВОДНОГО СУДНА СО ЛЬДОМ ПРИ ПОГРУЖЕНИИ // Современные проблемы науки и образования. 2015. № 1-2. ;URL: https://science-education.ru/ru/article/view?id=19842 (дата обращения: 04.03.2026).



