Оптические системы широко используются для решения ряда практических задач: получение информации о микромире (микроскопы), получение информации о мегамире (телескопы), фоторегистрация объектов на поверхности земли с помощью летательных аппаратов, фоторегистрация отдельных объектов, сцен с помощью фотоаппаратов, фотокамер. Основное ограничение связано с явлением дифракции света на входном зрачке оптических систем. Оно переводит точечные объекты в дифракционные максимумы, угловой размер которых зависит от апертуры входного зрачка оптической системы. Возможность разрешения двух светящихся точек определяется критерием Рэлея, согласно которому дифракционный максимум второй светящейся точки должен находиться на угловом расстоянии, превышающем половину углового размера основного дифракционного максимума первой светящейся точки /2,4/. При фоторегистрации протяженных объектов с помощью оптических систем явление дифракции искажает границы объектов и яркостный рельеф фотоизображения объектов. В настоящее время для уменьшения искажающего влияния дифракции при получении информации с помощью оптических систем, как правило, увеличивают апертуру входного зрачка. Однако размеры апертуры часто ограничены техническими возможностями.
В настоящей работе рассмотрены возможности цифровой обработки видеоизображений точечных источников света, в виде дифракционных максимумов, в оптических системах. Основой являются положения теории оптимального приема /5,6/, существенно дополненные разработками Балтийского федерального университета им. И.Канта (БФУ им. И.Канта) /3/. Дополнения касаются технологии решения задачи разрешения двух или более подобных сигналов. Функционал правдоподобия преобразовывается в другой вид, и его минимизация проводится методом перебора в пространстве неэнергетических параметров. Этим достигается высокое разрешение подобных сигналов.
Основные теоретические положения
Разрешающая способность оптических приборов ограничена явлением дифракции света. В результате дифракции на входном зрачке оптической системы точечный источник света преобразуется в протяженный объект – дифракционное распределение света. Угловая ширина главного максимума определяется известным выражением /2,4/:
![]() 1
1
Где ![]() длина волны,
длина волны, ![]() – радиус входного зрачка оптической системы.
– радиус входного зрачка оптической системы.
При наличии двух точечных источников света согласно критерию Рэлея их главные дифракционные максимумы будут наблюдаться раздельно, если угловое различие точечных источников ![]() . Таким образом, разрешающая способность оптических приборов ограничена предельным углом
. Таким образом, разрешающая способность оптических приборов ограничена предельным углом ![]() . Этим условием определяется разрешающая способность микроскопов, телескопов, глаза человека, т.е. всех оптических приборов, световой поток которых ограничен входным зрачком.
. Этим условием определяется разрешающая способность микроскопов, телескопов, глаза человека, т.е. всех оптических приборов, световой поток которых ограничен входным зрачком.
Рассмотрим технологию решения задачи оценки параметров вначале одного точечного источника света. Оптическая система преобразует световой поток в дифракционный максимум, который может быть представлен выражением.
![]() 2
2
Где ![]() – амплитуда напряженности поля светового потока,
– амплитуда напряженности поля светового потока, ![]() – угловое положение точечного источника света,
– угловое положение точечного источника света, ![]() – функция Бесселя первого порядка,
– функция Бесселя первого порядка,
![]() – волновое число.
– волновое число.
![]() – шумовая добавка. Она характеризуется нормальным распределением с дисперсией
– шумовая добавка. Она характеризуется нормальным распределением с дисперсией ![]() , средним значением, равным нулю и интервалом корреляции
, средним значением, равным нулю и интервалом корреляции ![]() . Запишем на основании (2) логарифм функции правдоподобия /3,5,6/:
. Запишем на основании (2) логарифм функции правдоподобия /3,5,6/:
![]() 3
3
Штрихами отмечены оценочные параметры сигнала.
Логарифм функции правдоподобия является условной плотностью распределения, максимум которой определяет наиболее правдоподобные оценки параметров сигнала. В связи с этим продифференцируем (3) по амплитуде ![]() и приравняем дифференциал нулю. В результате получим корреляционную функцию принятого сообщения и копии сигнала с единичной амплитудой:
и приравняем дифференциал нулю. В результате получим корреляционную функцию принятого сообщения и копии сигнала с единичной амплитудой:
![]() , 4
, 4
где ![]()
Максимум ![]() определяет оценку амплитуды
определяет оценку амплитуды ![]() и оценку углового положения
и оценку углового положения ![]() . Математическое ожидание от выражения (4) в максимуме является несмещенным:
. Математическое ожидание от выражения (4) в максимуме является несмещенным:
![]() 5
5
Оценим дисперсию параметров ![]() и
и ![]() . Для этого получим элементы двумерной информационной матрицы Фишера в соответствии с выражением (6) /3/:
. Для этого получим элементы двумерной информационной матрицы Фишера в соответствии с выражением (6) /3/:
![]() 6
6
Где ![]() – вектор параметров сигнала.
– вектор параметров сигнала.
В результате двойного дифференцирования логарифма функции правдоподобия согласно (6) по ![]() и
и ![]() получим информационную матрицу Фишера:
получим информационную матрицу Фишера:
![]() 7
7
Где ![]() ;
; ![]() ;
; ![]()
Коэффициенты ![]() равны нулю вследствие произведения симметричной и антисимметричной подинтегральной функции. Вычисляя диагональные элементы матрицы, обратной к информационной матрице Фишера, получим дисперсию амплитуды
равны нулю вследствие произведения симметричной и антисимметричной подинтегральной функции. Вычисляя диагональные элементы матрицы, обратной к информационной матрице Фишера, получим дисперсию амплитуды ![]() и дисперсию углового положения точечного источника
и дисперсию углового положения точечного источника ![]() :
:
![]() ;
; ![]() 8
8
Таким образом, метод максимального правдоподобия позволяет дать оценку углового положения точечного источника света. Эта оценка не зависит от размера дифракционного пятна. Она определяется с точностью, определяемой дисперсией углового положения источника света. Вместо дифракционного пятна (протяженного объекта) в результате данной обработки можно получить точечное изображение, угловое положение которого случайно и характеризуется дисперсией.
Рассмотрим случай дифракции двух точечных источников света на круглом отверстии радиуса ![]() . В этом случае распределение света в зависимости от угла дифракции будет представлено в виде суммы двух дифракционных максимума (сигнала) типа (2):
. В этом случае распределение света в зависимости от угла дифракции будет представлено в виде суммы двух дифракционных максимума (сигнала) типа (2):
![]() 9
9
Где ![]() – угловые положения точечных источников света.
– угловые положения точечных источников света. ![]() – амплитудные значения точечных источников света.
– амплитудные значения точечных источников света.
Обозначим для краткости записи:
![]() ;
; ![]() 10
10
и запишем логарифм функции правдоподобия на основании (9):
![]() 11
11
Штрихами отмечены оценочные параметры сигналов.
При наличии двух и более сигналов в принятом сообщении минимизация (11) не приводит к однозначному решению. Покажем это. Математическое ожидание от функционала правдоподобия равно следующему:
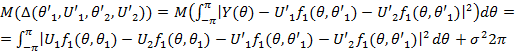 12
12
Подинтегральное выражение в (12) допускает ряд оценочных значений параметров сигналов минимизирующих функционал правдоподобия. Если сигнал в принятом сообщении один, то минимизация функционала правдоподобия (12) однозначна.
Дифференцируя (11) по ![]() и
и ![]() , и приравнивая дифференциалы нулю, получим систему уравнений правдоподобия:
, и приравнивая дифференциалы нулю, получим систему уравнений правдоподобия:
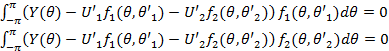 13
13
Используя эти уравнения, как условия, преобразуем логарифм функции правдоподобия к виду:
![]() 14
14
Математическое ожидание от преобразованного функционала правдоподобия приводит к однозначной его минимизации:
![]()
![]() 15
15
Амплитуды ![]() находятся при этом из уравнений правдоподобия (12):
находятся при этом из уравнений правдоподобия (12):
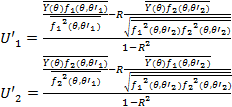 16
16
Где ![]() – нормированный коэффициент корреляции между двумя функциями.
– нормированный коэффициент корреляции между двумя функциями.
Черта сверху означает интегрирование по параметру ![]() .
.
Если угловое различие между дифракционными максимумами удовлетворяет критерию Рэлея (1), тогда коэффициент корреляции близок к нулю и выражения (16) совпадают с выражениями типа (4).
Если угловое различие меньше, чем определено в (1), тогда согласно классическим представлениям (критерий Рэлея) светящиеся точки сливаются вместе. Коэффициент корреляции в этом случае будет отличен от нуля и решения находятся по значению минимума поверхности функционала ![]() в двумерном пространстве углов
в двумерном пространстве углов ![]() и
и ![]() (14). В точке минимума поверхности функционала правдоподобия согласно (15) оценочные значения амплитуд и углов равны:
(14). В точке минимума поверхности функционала правдоподобия согласно (15) оценочные значения амплитуд и углов равны: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Оценим дисперсии углового положения двух светящихся точек и дисперсии их амплитудных значений напряженности поля. Для этого продифференцируем логарифм функции правдоподобия по параметрам ![]() и
и ![]() два раза. Получим элементы информационной матрицы Фишера:
два раза. Получим элементы информационной матрицы Фишера:
![]() 17
17
Где ![]() ,
, ![]() ,
, ![]() .
.
Определяя диагональные элементы матрицы, обратной к информационной матрице Фишера, получим дисперсии амплитуд от первой и второй светящихся точек ![]() ,
, ![]() :
:
![]() ,
, ![]() ,
, ![]() 18
18
Аналогично можно получить дисперсии угловых положений светящихся точек![]() ,
, ![]() . В этом случае информационная матрица Фишера будет:
. В этом случае информационная матрица Фишера будет:
![]() 19
19
Где![]() ,
, ![]() ,
, ![]()
Определяя диагональные элементы обратной матрицы, получим:
![]() ,
, ![]() ,
, ![]() 20
20
Таким образом, дисперсии угловых положений светящихся точек зависят от отношений сигнал/шум и взаимной корреляции дифракционных максимумов. Дисперсии будут минимальны, когда ![]() = 0. Однако, если отношение сигнал/шум достаточно большое (более 15 дБ), тогда при приемлемых дисперсиях коэффициент корреляции может достигать значения 0.9 и выше. Это сильно перекрывающиеся дифракционные максимумы.
= 0. Однако, если отношение сигнал/шум достаточно большое (более 15 дБ), тогда при приемлемых дисперсиях коэффициент корреляции может достигать значения 0.9 и выше. Это сильно перекрывающиеся дифракционные максимумы.
Предварительные результаты модельных расчетов
Изложим результаты предварительных модельных исследований вопросов разрешения двух точечных источника света. На рис.1 показаны два дифракционных максимума, полученных при следующих параметрах: амплитуды сигналов![]() ,
, ![]() , угловые положения источников света
, угловые положения источников света![]() – меняется линейно от значения
– меняется линейно от значения ![]() до
до ![]() с шагом
с шагом ![]() . При этом обеспечивается условия ортогональности двух дифракционных максимумов (
. При этом обеспечивается условия ортогональности двух дифракционных максимумов (![]() и условия неортогональности (
и условия неортогональности (![]() ). Относительный размер входного зрачка системы
). Относительный размер входного зрачка системы ![]() .
.
На рис. 1 дифракционные максимумы находятся в области их ортогональности (![]() . Максимумы и их положения позволяют оценить (точечная оценка) амплитуды и угловые положения двух точечных источников света:
. Максимумы и их положения позволяют оценить (точечная оценка) амплитуды и угловые положения двух точечных источников света:
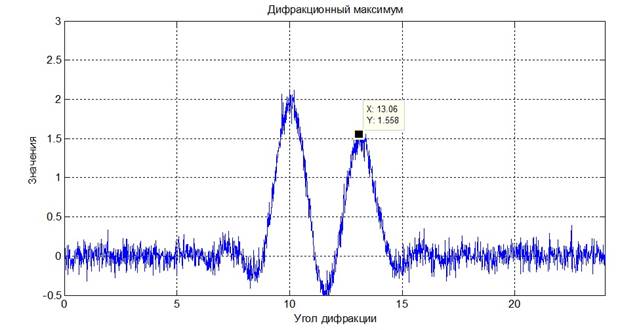
Рис.1. Дифракционные максимумы двух точечных источника света
На рис. 2 показаны два дифракционных максимума в области их неортогональности, когда угловые положения равны ![]() . Разрешить источники света в этом случае согласно критерию Рэлея невозможно:
. Разрешить источники света в этом случае согласно критерию Рэлея невозможно:
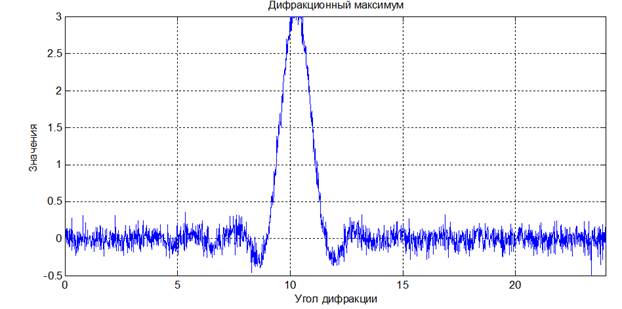
Рис. 2. Два дифракционных максимума в области их неортогональности (Ө1=100,Ө2=10.80). Максимумы сливаются
Возможность решения задачи разрешения двух точечных источника света методом максимального правдоподобия, как в области ортогональности, так и в области неортогональности дифракционных максимумов, показана на рис. 3. По горизонтальной оси отложена разность между угловыми положениями источников света в градусах. По вертикали показаны оценки углового положения первого источника света (![]() ) и оценки линейно меняющихся угловых положений второго источника света: (
) и оценки линейно меняющихся угловых положений второго источника света: (![]() ).
).
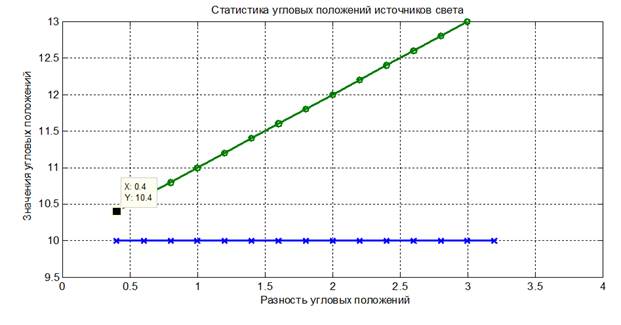
Рис.3. Зависимость угловых положений источников света от разности угловых положений
Как видно из рисунка два источника света вполне разрешаются даже при угловом различии ![]() . Это соответствует коэффициенту корреляции между дифракционными максимумами ~0.9.
. Это соответствует коэффициенту корреляции между дифракционными максимумами ~0.9.
На рис. 4 показаны раздельные оценки амплитуд двух точечных источников света при использовании метода максимального правдоподобия:
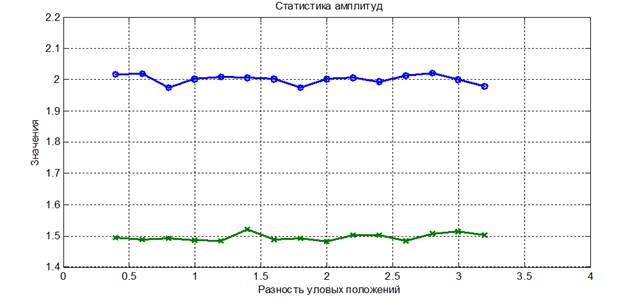
Рис. 4. Оценки амплитуд в зависимости от разности угловых положений точечных источников света
Таким образом, с помощью модельных расчетов показано, что метод максимального правдоподобия обеспечивает увеличения разрешения двух точечных источников света в оптических системах в ~4 раза по сравнению с Рэлеевским разрешением.
Заключение
Изложим кратко результаты настоящей работы.
1. На основе положения теории оптимального приема создан метод обработки дифракционных максимумов, позволяющий увеличить разрешающую способность оптических систем:
- получены основные выражения, определяющие оптимальный алгоритм обработки дифракционных максимумов;
- получены выражения для дисперсии оценочных параметров точечных источников света.
2. Показано с помощью модельных расчетов, что созданный метод обработки позволяет увеличить разрешение двух точечных источника света в оптических системах по сравнению с Рэлеевским разрешением в ~4 раза.
Рецензенты:
Захаров В.Е., д.ф.-м.н., профессор, заведующий кафедрой радиофизики и информационной безопасности Балтийского федерального университета им. И. Канта Минобрнауки, г. Калининград;
Никитин М.А., д.ф.-м.н., профессор, профессор кафедры физики БФУ им. И. Канта, г. Калининград.
Библиографическая ссылка
Мешков С.С., Бабинович А.И., Пахотин В.А. ЦИФРОВАЯ ОБРАБОТКА ВИДЕОИЗОБРАЖЕНИЙ ОТДЕЛЬНЫХ СВЕТЯЩИХСЯ ТОЧЕК В ОПТИЧЕСКИХ СИСТЕМАХ // Современные проблемы науки и образования. 2015. № 1-2. ;URL: https://science-education.ru/ru/article/view?id=19820 (дата обращения: 26.02.2026).



