Применение базисов безизбыточной системы оснований ПСКВ в цифровой обработке сигналов позволяет повысить скорость и точность обработки, кроме того, ПСКВ увеличивает информационную надежность за счет обнаружения ошибки и ее коррекции.
Если на диапазон возможного изменения кодируемого множества полиномов наложить ограничения, то есть выбрать k из n оснований ПСКВ (k<n), то это позволит осуществлять разбиение полного диапазона ![]() расширенного поля Галуа
расширенного поля Галуа ![]() на два непересекающихся подмножества.
на два непересекающихся подмножества.
Первое подмножество называется рабочим диапазоном и определяется выражением
![]()
Многочлен ![]() с коэффициентами из поля
с коэффициентами из поля ![]() будет считаться разрешенным в том и только в том случае, если он является элементом нулевого интервала полного диапазона
будет считаться разрешенным в том и только в том случае, если он является элементом нулевого интервала полного диапазона ![]() , то есть принадлежать диапазону
, то есть принадлежать диапазону ![]() .
.
Второе подмножество ![]() , определяемое произведением
, определяемое произведением ![]() контрольных оснований
контрольных оснований ![]() ,
,
задает совокупность запрещенных комбинаций. Если ![]() является элементом второго подмножества, то считается, что данная комбинация содержит ошибку. Таким образом, местоположение полинома
является элементом второго подмножества, то считается, что данная комбинация содержит ошибку. Таким образом, местоположение полинома ![]() относительно двух данных подмножеств позволяет однозначно определить, является ли кодовая комбинация
относительно двух данных подмножеств позволяет однозначно определить, является ли кодовая комбинация ![]() разрешенной, или содержит ошибочные символы.
разрешенной, или содержит ошибочные символы.
Нулевизация заключается в последовательном вычитании из исходного полинома, представленного в модулярном коде, некоторых минимальных полиномов - констант нулевизации таких, что полином А(z)последовательно преобразуется в полином вида
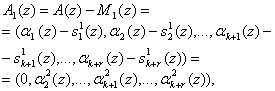
где
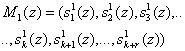 - константа нулевизации по первому основанию p1(z).
- константа нулевизации по первому основанию p1(z).
Затем из полученный результата вычитается следующая константа нулевизации для получения полинома
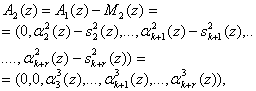
где
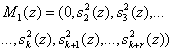 - константа нулевизации по второму основанию p2(z),
- константа нулевизации по второму основанию p2(z),
и так далее. Продолжая данный процесс в течение k итераций, получается
![]() .
.
Применение метода нулевизации позволяет последовательно получать наименьший полином, кратный сначала ![]() , затем полином – кратный
, затем полином – кратный ![]() , и в конечном итоге – кратный рабочему диапазону
, и в конечном итоге – кратный рабочему диапазону ![]() .
.
Если в результате последовательного выполнения процедуры нулевизации будет получен нулевой результат, т.е. xk+1(z)=0, xk+2(z)=0, …, xk+r(z)=0,
то это свидетельствует, что исходная комбинация A(z), представленная в модулярном коде, не содержит ошибок. В противном случае – модулярный код A(z) – содержит ошибки.
Основным недостатком метода нулевизации является последовательный характер вычислительного процесса. Это обусловлено прежде всего тем, что константы нулевизации представляют собой наименьшие возможные числа вида:
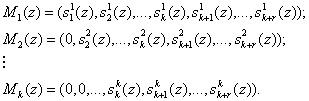
где
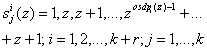 .
.
Повысить скорость выполнения процедуры нулевизации можно за счет модификации констант нулевизации ![]() . Оставляя неизменным условие невыхода константы нулевизации
. Оставляя неизменным условие невыхода константы нулевизации ![]() за пределы рабочего диапазона
за пределы рабочего диапазона ![]() , возьмем в качестве последних значения произведение остатков рабочих оснований на величину ортогональных базисов безизбыточной системы оснований
, возьмем в качестве последних значения произведение остатков рабочих оснований на величину ортогональных базисов безизбыточной системы оснований
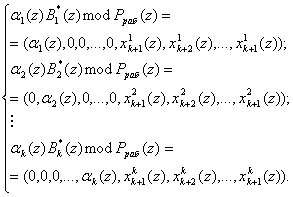
где ![]() - ортогональный базис, безизбыточной системы оснований; i=1,2,…,k.
- ортогональный базис, безизбыточной системы оснований; i=1,2,…,k.
Тогда если положить условие, что ![]() , где
, где ![]() , то полином
, то полином ![]() согласно китайской теореме об остатках (КТО) можно представить в виде
согласно китайской теореме об остатках (КТО) можно представить в виде
![]() .
.
Каждое слагаемое выражения (9) представляет собой:
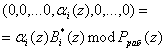 ,
,
Подставим выражения (8) в равенство (10). Получаем:
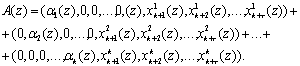
Следовательно, значения остатков по контрольным основаниям будут определяться
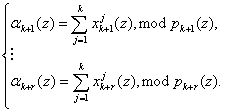
Значит, разность полинома A(z) и модифицированных констант нулевизации ![]() , i=1, 2,…, k, псевдоортогональных форм, полученных согласно (4.5), задаёт величину нормированного следа полинома
, i=1, 2,…, k, псевдоортогональных форм, полученных согласно (4.5), задаёт величину нормированного следа полинома
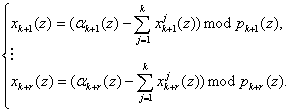
Исходя из условия, что модифицированные константы нулевизации ![]() представляют собой ортогональные базисы безизбыточной системы оснований ПСКВ, то операция нулевизации (13) может быть реализована параллельно.
представляют собой ортогональные базисы безизбыточной системы оснований ПСКВ, то операция нулевизации (13) может быть реализована параллельно.
Для уменьшения объема хранимых значений констант нулевизации ![]() , i=1, 2,…, k, представим остатком числа αi(z) в виде:
, i=1, 2,…, k, представим остатком числа αi(z) в виде:
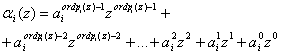 ,
,
где ![]() элементы поля GF(2); j =0, 1, …, ord pi(z)-1.
элементы поля GF(2); j =0, 1, …, ord pi(z)-1.
Тогда справедливо:
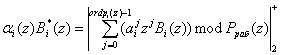 .
.
Поэтому вместо хранения ![]() констант нулевизации
констант нулевизации ![]() достаточно определить ord pi(z) констант.
достаточно определить ord pi(z) констант.
Таким образом, два контрольных основания позволяют 100% обнаружить ошибку, а одно контрольное основание – 95% обнаружения ошибки.
Библиографическая ссылка
Калмыков И.А., Емарлукова Я.В. ОБНАРУЖЕНИЕ И КОРРЕКЦИЯ ОШИБОК В КОДАХ ПОЛИНОМИАЛЬНОЙ СИСТЕМЫ КЛАССОВ ВЫЧЕТОВ НА ОСНОВЕ НУЛЕВИЗАЦИИ // Современные проблемы науки и образования. 2006. № 2. ;URL: https://science-education.ru/ru/article/view?id=197 (дата обращения: 05.03.2026).



