Известно, строгого решения поставленной задачи не имеется. Теория конусообразования Маскета – Чарного исходит из допущения, что отклонение поверхности раздела двух фаз от первоначальной плоской формы не влияет на распределение потенциала скоростей фильтрации в нефтяной части пласта [1, 2]. Строгое решение было бы возможным, если бы был известен профиль конуса. Еще большие трудности представляет задача о предельных безводных дебитах газовых скважин в условиях нелинейного закона фильтрации, когда решения о распределении потенциала вообще не имеется.
Обычно в таких случаях безразмерный предельный безводный дебит для газовой скважины определяют по нефти, а предельную депрессию рассчитывают по хорошо известной двухчленной формуле для нелинейного закона фильтрации. Это первое допущение. Вторым допущением при этом является то, что добавочные фильтрационные сопротивления принимаются из решения притока к несовершенной скважине, что ведет к завышению предельных размерных дебитов.
Для более строгого подхода к решению этой задачи добавочные фильтрационные сопротивления надо принимать из условия предельно- устойчивого границы двух жидкостей. Рассмотрим эту задачу.
Принимаем двухзонную схему притока (см. рисунок 1). Для зоны пространственного притока I имеем дифференциальное уравнение ![]() .
.
Умножая левую и правую части на плотность газа ρ(Р) и выражая ее по уравнению состояния реального газа в осредненных параметрах вязкости ![]() и коэффициента сверхсжимаемости газа Z(
и коэффициента сверхсжимаемости газа Z(![]() , разделяя переменные, в интегральной форме получаем:
, разделяя переменные, в интегральной форме получаем:
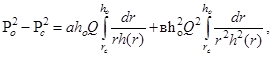 (1)
(1)
где
![]() (2)
(2)
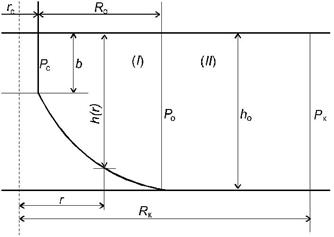
Рис.1. Двухзонная схема притока к несовершенной скважине, обусловленного нелинейным законом фильтрации
Границу![]() раздела в вертикальном сечении (конус) будем аппроксимировать специальной функцией, изображение которой называется «Локоном Аньези» [1]
раздела в вертикальном сечении (конус) будем аппроксимировать специальной функцией, изображение которой называется «Локоном Аньези» [1]
![]() (3)
(3)
Zo – ордината вершины конуса в предельно-устойчивом положении (см. рисунок), определяемая для соответствующего безразмерного предельного дебита [2, 3, 4, 5].
В формулах (2) l – коэффициент макрошероховатости, остальные обозначения общеприняты. Внося (3) в (1), интегрируя и делая ряд преобразований, получаем:
![]() (4)
(4)
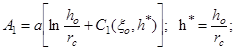 (5)
(5)
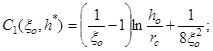 (6)
(6)
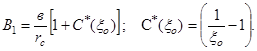 (7)
(7)
Для зоны плоско-радиального притока II (см. рисунок) имеем:
![]() (8)
(8)
![]() (9)
(9)
Решая совместно (4) и (8) и учитывая (5) и (9), получаем:
![]() (10)
(10)
где
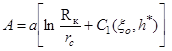 ; (11)
; (11)
![]() (12)
(12)
Чтобы рассчитать предельную депрессию по формуле (8), необходимо вначале определить предельный безводный дебит Q=Qпр.
В соответствии с формулой (19) для двухзонной схемы притока (при m=1 и Ro=ho) имеем:
![]() ;
; ![]() ∆ρ=ρв-ρг; (13)
∆ρ=ρв-ρг; (13)
![]()
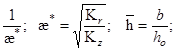
где:
q(ρ,![]() ) – безразмерный предельный безводный дебит, определяемый по таблицам или графикам [3, 4, 5];
) – безразмерный предельный безводный дебит, определяемый по таблицам или графикам [3, 4, 5];
ρв и ρг – плотности воды и газа в пластовых условиях.
Внося (13) в (10) и учитывая (11), (12) и (2), после ряда преобразований получаем формулу для расчета предельной депрессии в виде:
![]() (14)
(14)
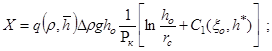 (15)
(15)
![]() . (16)
. (16)
Преимущество формулы (14) перед другими известными состоит в том, что она учитывает добавочные фильтрационные сопротивления, обусловленные предельно-устойчивым положением конуса подошвенной воды, и уточняет результаты расчета путем использования двухзонной схемы притока, что в конечном счете приводит к увеличению расчетных значений предельного дебита Qпр и предельной депрессии ∆Рпр.
Проанализируем формулы добавочных фильтрационных сопротивлений (6) и (12), обусловленных относительным вскрытием, по линейному и нелинейному законам фильтрации на конкретном примере. Принимаем исходные данные: ho=10 м; rс=0,1 м; ρ=1; ![]() =0,5;
=0,5; ![]()
По таблице [3, 4, 5] находим безразмерный предельный дебит ![]() и соответствующую ему безразмерную ординату вершины конуса
и соответствующую ему безразмерную ординату вершины конуса ![]() , что составляет размер высоты вершины от ГВК Ук=3,25 м. По формуле (6) определяем С1(
, что составляет размер высоты вершины от ГВК Ук=3,25 м. По формуле (6) определяем С1(![]() =1,629; по формуле (12) имеем С2(
=1,629; по формуле (12) имеем С2(![]() =1,307.
=1,307.
По таблице [6, 7] определяем фильтрационные сопротивления, обусловленные притоком к несовершенной скважине, с любым дебитом: С1(![]() и
и ![]() .
.
Как видим, завышение последних над первым и в данном примере в 2 раза. Очевидно, и в других случаях завышение останется существенным. Такое явление вполне объяснимо. При дебитах выше предельных деформированная поверхность раздела двух жидкостей, относительно быстро продвигаясь по оси скважины, претерпевает «точку возврата» [2] и начинается прорыв воды к забою, вызывающий большие фильтрационные сопротивления. В то время как, предельные безводные дебиты, значительно уменьшающие скорости фильтрации, обеспечивают плавное обтекание «холмообразного» поднятия первоначально плоского раздела двух жидкостей, резко снижая фильтрационные сопротивления.
Интересно отметить и тот факт, что фильтрационное сопротивление (6), характеризующее приток по линейному закону, также является функцией одних и тех же параметров (![]() , что и при притоке к несовершенной скважине с какими угодно дебитами. Фильтрационное сопротивление С2(
, что и при притоке к несовершенной скважине с какими угодно дебитами. Фильтрационное сопротивление С2(![]() оказывается по величине обратно пропорциональной величине ординаты вершины конуса
оказывается по величине обратно пропорциональной величине ординаты вершины конуса ![]() , которая определяется относительным вскрытием
, которая определяется относительным вскрытием ![]() Чем меньше
Чем меньше ![]() тем меньше
тем меньше ![]()
Следует заметить, что в приведенном нами примере пласт принимался однородно-изотропным, т.е. коэффициент анизотропии æ*=1 при ![]() =Ro/æ* ho=1 (Rо=hо). М. Маскет и И. А. Чарный при ρ≥1 рекомендуют принимать размер зоны пространственного движения, равным Rо=1÷2hо.
=Ro/æ* ho=1 (Rо=hо). М. Маскет и И. А. Чарный при ρ≥1 рекомендуют принимать размер зоны пространственного движения, равным Rо=1÷2hо.
Исследуем формулу (3), записав ее в безразмерном виде:
![]() (17)
(17)
где:
![]() (18)
(18)
Принимаем æ*=2, тогда зона пространственного движения Rо=5 м при толщине пласта hо=10 м; при ![]() м и
м и ![]() получаем
получаем ![]() =0,9846, следовательно,
=0,9846, следовательно, ![]() м. Как видим, практически уравнение (17) условию на контуре зоны пространственного движения удовлетворяет. При
м. Как видим, практически уравнение (17) условию на контуре зоны пространственного движения удовлетворяет. При ![]() из (17), получаем
из (17), получаем ![]() т.е. получаем точно размер ординаты вершины конуса.
т.е. получаем точно размер ординаты вершины конуса.
Выводы
Рассмотренный метод существенно уточняет решение задач теории конусообразования, позволяет построить профиль конуса, оценить остаточные запасы углеводородов в удельном объеме дренирования и определить приближенно зону пространственной фильтрации в анизотропных пластах. Функция (17), называемая «Локон Аньези», вполне приемлема для описания профиля конуса воды в предельно устойчивом состоянии.
Рецензенты:
Грачев С. И., д.т.н., профессор, заведующий кафедрой «Разработка и эксплуатация нефтяных и газовых месторождений», Институт геологии и нефтегазодобычи, ФГБОУ ВПО ТюмГНГУ, г. Тюмень;
Леонтьев С. А., д.т.н., профессор, профессор кафедры «Разработка и эксплуатация нефтяных и газовых месторождений», Институт геологии и нефтегазодобычи, ФГБОУ ВПО ТюмГНГУ, г. Тюмень.
Библиографическая ссылка
Каширина К.О. МЕТОДИКА РАСЧЕТА ДОБАВОЧНЫХ ФИЛЬТРАЦИОННЫХ СОПРОТИВЛЕНИЙ, ОБУСЛОВЛЕННЫХ ПРЕДЕЛЬНО-УСТОЙЧИВЫМ ПОЛОЖЕНИЕМ КОНУСА ПОДОШВЕННОЙ ВОДЫ, И ПРЕДЕЛЬНОЙ ДЕПРЕССИЕЙ ПРИ НЕЛИНЕЙНОМ ЗАКОНЕ ФИЛЬТРАЦИИ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=19659 (дата обращения: 12.03.2026).



