При вытеснении вязкопластичной нефти (ВПН) теплоносителями, как известно, образуются две области (зоны): в первой, происходит вытеснение холодной неразогретой нефти теплоносителем; во второй, вытесняется разогретая нефть. Считается, что первая зона определяется гидродинамическим фронтом вытеснения, вторая – тепловым фронтом. Первый фронт вытеснения опережает второй. Во второй зоне вытеснения «горячая» нефть изменяет первоначальные физические свойства: плотность, динамическая вязкость, начальный градиент давления нефти уменьшаются, коэффициент подвижности нефти возрастает.
Для практических инженерных расчетов и моделирования процессов вытеснения пользуются лабораторными данными, характеризующими зависимости физических свойств нефти от температуры. Для теоретических приложений удобнее использовать функциональные зависимости, которые качественно описывают изменение параметров, что не всегда соответствуют полученным экспериментальным значениям. Поскольку начальный градиент давления и вязкость зависят от температуры, то для определения поля температур в зоне 2 возникает необходимость решения системы уравнений параболического типа, описывающего распределение температуры, и трансцендентных уравнений, характеризующих зависимость физических параметров от температуры.
Изменение температуры в пласте при закачке теплоносителя зависит от пространственных координат и времени.
Уравнение теплопроводности в общем виде имеет вид:
(1)
, 
, 
(2)
где vn,vb – скорости фильтрации нефти и воды; g – начальный градиент давления в зоне совместной фильтрации; λT – коэффициент теплопроводности; k – коэффициент абсолютной проницаемости; kb* , kn* – относительные фазовые проницаемости; μn,b(T) – коэффициенты динамической вязкости нефти и воды.
где сb, cn, cTf – удельные теплоемкости воды, нефти и твердой фазы; ρb , ρn, ρTf – плотности воды, нефти и твердой фазы; T – температура в зоне 2; s – коэффициент водонасыщенности; m – коэффициент пористости; vT – скорость распространения тепла за счет теплопроводности.
Распределение давлений нефти и воды в зоне теплового воздействия 2 для плоскорадиальной фильтрации определяется из уравнения аналогичного уравнению пьезопроводности В.Н. Щелкачева
. (3)
Здесь i=b,n соответствуют воде и нефти, pi – давления воды и нефти, ϰi – коэффициенты пьезопроводности воды и нефти, зависящие от динамической вязкости. Если начало координат совпадает с забоем нагнетательной скважины, то 
меньше нуля. Поэтому в скобках взят знак «+». Заметим, что термин начальный градиент давления справедлив только в том случае, когда g постоянен, не зависит от температуры. В данном случае это величина переменная и зависит от температуры
(4)
где ΔТ=Т-Т0, Т0 – начальная пластовая температура; g0 – начальный градиент давления, соответствующий изотермическому процессу и определяемый либо лабораторными методами, либо в результате обработки гидродинамических исследований скважин. Второе более достоверно [2]. Параметр αg – определяется по результатам интерпретации лабораторных исследований. По данным сотрудников Ухтинского госуниверситета αg=0,1-0,4 1/град.
Для поршневого вытеснение нефти уравнение (1) примет вид:
Здесь 
– коэффициент температуропроводности за счет теплопроводности, 
– коэффициент, учитывающий изменение температуры в результате конвекции.
Запишем искомое уравнение в цилиндрических координатах, при условиях: Т не зависит от угловой координаты, сжимаемостью воды пренебрегаем
(5)
В отличие от модели Ловерье в уравнении (5) учитывается изменение температуры пласта по вертикали – толщине пласта. Зададимся постоянным потоком тепла qT на забое нагнетательной скважины. Решая (5) методом интегральных преобразований [3], получим
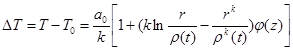(6)
,
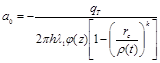(7)
Здесь qT – скорость теплового потока, кДж/с; h –половина толщины пласта; k,n – числовые параметры, определяемые из сопоставления фактических и расчетных данных; ρ(t) – радиус теплового фронта (при r≤ρ(t) горячей водой вытесняется разогретая нефть с меньшей вязкостью); rc – радиус скважины. 
, m – коэффициент открытой пористости; s – коэффициент водонасыщенности; λn,λb – коэффициенты теплопроводности нефти и воды. Заметим, что интегрирование (5) необходимо для определения переменного радиуса фронта теплового вытеснения, но это уже другая статья.
Подставляя (6) в (4), после преобразований, получим зависимость g от координат и времени:
, 
, 
(8)
В зоне 2 теплового вытеснения 
r изменяется в интервале от rc до ρ(t). При r=ρ(t) и z=0 функция F имеет максимум, F(ρ(t),o,t)=1 и g=g0. При z=h, что соответствует кровле пласта φ*=0,75, r=ρ2(t), F(ρ2(t),h,t)=1, причем ρ(t)>ρ2(t) . Тепловое вытеснение на кровле пласта (z=h) отстает от теплового вытеснения на нейтральной линии (z=0). Минимальное значение функция F принимает при r=rc на забое нагнетательной скважины.
Отметим, что функция F и ее производная работают только в зоне 2 теплового вытеснения, и при r≥ρ(t) тождественно равны: F=1, F/r=0.
Изменения градиента g как функции координат приведены в таблице 1.
Пример 1. Дано αg=0,11/град, g0=0,45МПа/м, qT=8кДж/с,λ1=0,0043 кДж/(м*с*град),ρ(t)=100м, к=2, h=10м, rc=0,1м, 
.
Таблица 1
Изменения градиента g как функции координат
|
|
x |
0,001 |
0,01 |
0,05 |
0,1 |
0,25 |
0,623 |
0,75 |
1 |
||
|
z |
a0 |
β0 |
ϕ(z) |
g, МПа/м |
|||||||
|
0 |
-31,20 |
1,56 |
1,00 |
9,3E-10 |
1,2E-06 |
1,9E-4 |
0,0016 |
0,026 |
0,268 |
0,363 |
0,45 |
|
10 |
-41,61 |
2,08 |
0,75 |
1,6E-09 |
2,1E-06 |
3,9Е-4 |
0,0027 |
0,043 |
0,45 |
|
|
Вблизи забоя нагнетательной скважины g практически равен нулю, фильтрация происходит по закону Дарси. По мере удаления к забоям добывающих скважин значения градиента g возрастают, скорость фильтрации подчиняется обобщенному закону Дарси с учетом начального градиента (2). Здесь g является величиной переменной, определяемой соотношением (8).
Другими физическими параметрами, существенно зависящим от изменения температуры, являются коэффициенты динамической вязкости. Необходимость подобных исследований возникает при непоршневом вытеснении нефти теплоносителем. Из уравнения (1) видно, что скорости фильтрации нефти и воды (2) в разогретой зоне 2 оказывает влияние на распределения поля температур и на продвижение теплового фронта вытеснения.
Для определения зависимости μn от координат воспользуемся исследованиями профессора В.И. Кудинова и его сотрудников о зависимости вязкости нефти Гремихинского месторождения от температуры, начальная температура равна 280С, начальная вязкость 116 мПас. На рис.3 [4] выделена область эффективных температур залежи А-4, соответствующая интервалу 60-700 С, при T > 700C вязкость изменяется незначительно. Функциональная зависимость вязкости от температуры не приводится. Анализируя имеющиеся результаты, на графике можно выделить три участка: первый – соответствующий низким температурам, второй – соответствующий области эффективных температур, третий – соответствующий высоким температурам. Исходя из вышесказанного, функциональную зависимость динамической вязкости от ΔТ, представим в виде трех экспоненциальных функций:
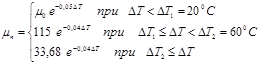или 
(10)
где μ0 – динамическая вязкость холодной нефти; aμi, αμi – параметры, определяемые интерпретацией лабораторных замеров. Третья формула (10) i=3 соответствует призабойной зоне пласта нагнетательной скважины. По мере удаления от ПЗП температура уменьшается до области эффективных температур i=2, вязкость рассчитывается по второму соотношению (10). Наконец вблизи теплового фронта вытеснения r≤ρ(t) работает первая формула (10).
После преобразований получим формулы аналогичные (8) i=1,2,3:
, 
, 
(11)
Поскольку вязкость в (2) стоит в знаменателе, то для расчетов удобнее пользоваться обратными функциями,
.
По данным [5] динамическая вязкость закачиваемой в пласт горячей воды гораздо меньше, чем вязкость в нормальных условиях μb0 Изменение динамической вязкости воды зависит от давления, минерализации и может уменьшиться с ростом температуры до пяти раз. В связи с этим на скорость фильтрации закачиваемой воды будет существенно влиять изменение температуры, которое по аналогии с предыдущим получим в виде:
, 
, 
,
Обратная функция Fb* равна
(12)
Рассмотрим произведение функций Φ(x,z)=F(x,z)*Fb*(x,z), которое будет использовано в дальнейшем, 
.
(13)
График функции приведен на рисунке 1. Данные для расчетов взяты из примера 1, αb=0,012 1/С0. Наименьшее значение Φ(x,z) соответствует 
отлично от нуля, максимальное – при 
, равно 1 имеет место на границе теплового фронта. Причем при z=h, на кровле пласта, максимум Φ(x,z) достигается с запаздыванием. Производная функции по r ведет себя также как и производная функции F(x,z).
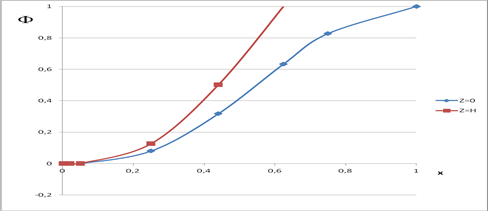
Рис. 1. График функции Φ(x,z) для z=0 и z=h
При закачке в пласт теплоносителя должны соблюдаться соотношения между физическими свойствами горячей воды, ФЕС пласта и технологическими показателями: приемистостью Q, скоростью теплового потока qT . Для вывода таких соотношений используем непрерывность скорости фильтрации закачиваемой в пласт воды 
Градиент давления в зонах возмущения 1 и 2 при постоянной приемистости на забое нагнетательной скважины Q по аналогии с решением, приведенным в [6], имеет вид:
Для ρ(t) ≤r≤ρb(t) g=g0, для rc ≤r≤ρ(t) g=g0F(r,z). Здесь ρb(t) – радиус гидродинамического фронта вытеснения, ρ(t) – радиус теплового фронта вытеснения. Скорость фильтрации vr на границах фронтов вытеснения и на забое нагнетательной скважины. Для r=ρb(t) и g=g0 vr=0. Значения vr(ρ) и vr(rc) должны быть больше нуля. В результате получим
, (14)
Где kb – коэффициент фазовой проницаемости воды, 
>2 – отношение радиусов гидродинамического и теплового фронтов вытеснений.
В работе [7] приведена формула, связывающая приемистость и скорость теплового потока 
, где сb, ρplb – удельная теплоемкость и плотность воды соответственно. После подстановки в (15), получим условие, связывающее технологические показатели и физические параметры:
(15)
Пример 2. Пусть kb =200*10-15м2, сb=4,15кДж/(кг*град), ρplb=1000(кг/м3), ΔТс=3000 С, остальные необходимые данные берутся из примера 1. После расчетов получим, что условия (14) и (15) выполняются для Q> 40м3/сут.
Зачем нужны условия (14)-(15)? Еще в середине 50-х годов прошлого века один из сотрудников Н.Винера доказал теорему, что для любой программы (программного продукта) найдется такой набор входных (исходных) данных, что полученный результат будет неверный. Поэтому для предварительной оценки и моделирования физических процессов следует проводить проверку на совместимость вводимых физических параметров.
Рассмотренное тепловое вытеснение нефти в однородном пласте по модифицированной модели Ловерье, может быть обобщено для неоднородного по проницаемости пласта, состоящего из гидродинамически несвязанных прослоев. При наличии гидродинамической связи, кроме изменения температуры по толщине пласта, следует учитывать функции перетоков флюидов между пропластками разной проницаемости.
Рецензенты:
Грачев С.И., д.т.н., профессор, заведующий кафедрой «Разработка и эксплуатация нефтяных и газовых месторождений», Институт геологии и нефтегазодобычи, ФГБОУ ВПО ТюмГНГУ, г. Тюмень;
Леонтьев С.А., д.т.н., профессор, профессор кафедры «Разработка и эксплуатация нефтяных и газовых месторождений», Институт геологии и нефтегазодобычи, ФГБОУ ВПО ТюмГНГУ, г. Тюмень.
Библиографическая ссылка
Коротенко В.А., Кушакова Н.П., Забоева М.И., Александров М.А. ЗАВИСИМОСТЬ ФИЗИЧЕСКИХ ПАРАМЕТРОВ ВЯЗКОПЛАСТИЧНОЙ НЕФТИ ОТ ТЕРМОБАРИЧЕСКИХ УСЛОВИЙ И КООРДИНАТ // Современные проблемы науки и образования. – 2015. – № 1-1. ;URL: https://science-education.ru/ru/article/view?id=19657 (дата обращения: 25.04.2024).