Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Каширина К.О. 1

---

1 ФГБОУ ВПО «Тюменский государственный нефтегазовый университет»

Задача притока пластовых жидкостей к горизонтальным скважинам, дренам и трещинам рассматривалась многими авторами в различной постановке. Совместное развитие техники бурения и технологии эксплуатации горизонтальных скважин сделало вполне реальным их широкое практическое применение с существенной технико-экономической эффективностью. Горизонтальное бурение всё ещё остаётся проблематичным делом, требующее во многих нефтедобывающих регионах проводить сравнительные технико-экономические анализы для скважин с вертикальными и горизонтальными стволами. Представленная методика рекомендуется при составлении проектов разработки месторождений и в условиях интенсивного существующего горизонтального бурения. В отличие от вертикальных скважин проблема притока к горизонтальным стволам является более сложной в виду неоднородности характера линий тока в области дренирования. Имеющиеся аналитические решения о притоке жидкости и газа к горизонтальным стволам и несовершенным галереям (вертикальным трещинам) требуют тщательного их анализа и изучения с тем, чтобы обосновано использовать то или иное решение в конкретной ситуации.

Статья в формате PDF

184 KB

сетка горизонтальных скважин

вертикальные трещины ГРП

оптимальные размеры сетки

1. Азиз Х., Сеттери Э. Математическое моделирование пластовых систем. – М., Недра. – 1982. – 408 с.

2. Вахитов Г. Г. И др. Освоение месторождений с помощью многозабойных горизонтально-разветвлённых скважин. В сб. “Исследования в области технологии и техники добычи нефти”. ВНИИ. – М., 1976. – Вып. 54. – С. 3-14.

3. Выбор геометрии рационального размещения горизонтальных скважин в пласте. – ЭИ, серия: Нефтепромысловое дело (заруб. опыт). – ВНИИОНГ – 1994. – вып. 7. – С. 1-11 (Реферат ст. Suprinovich R., Butler R. M. The choice of pattent size and shape for regular arrays of horizontal wells // J. of Canad. Thecnol. – 1992, 1. – Vd.31, №1. – p. 39-44).

4. Европейцев Р. К. и др. О строительстве в Западной Сибири первой горизонтальной скважины // «Нефтепромысловое хозяйство». – 1986. - №12. – С. 8-12.

5. Леви Б. И., Темнов Г. Н., Евченко В. С., Санкин В. М. Применение горизонтальных скважин на месторождениях ПО Красноленинскнефтегаз. Обзор инф. сер. «Нефтепромысловое дело». – М.: ВНИИОНГ, 1993. – 69 с.

6. Телков А. П., Краснова Т. Л. Расчёт оптимального положения и дебита горизонтальной скважины, дренирующей нефтегазовую залежь с подошвенной водой.// Геология, геофизика и разработка нефтяных месторождений. – 1997. - №6. – С. 34.

На основании имеющихся теоретических исследований и накопленного практического опыта многие авторы выделяют следующие основные объекты, которые целесообразно разрабатывать горизонтальными стволами: маломощные пласты (5...10 м) с низкой проницаемостью с целью увеличения коэффициента продуктивности; нефтенасыщенные пласты с подошвенной водой и верхним газом с целью ограничения прорыва конусов воды и газа и увеличения коэффициента извлечения; трещиновато-пористые пласты с развитой вертикальной трещиноватостью; залежи высоковязких нефтей и битумов, шельфовые и труднодоступные продуктивные зоны; залежи, в которых осуществляется поддержание пластового давления с целью создания эффективного линейного фронта вытеснения.

Одним из основных вопросов является обоснование рациональной геометрии области дренирования, т. е. оптимизация сетки размещения горизонтальных стволов. Кроме того, выбор протяжённости горизонтального ствола также требует реального обоснования, зависящего от применяемого оборудования при бурении, конструкции скважины, характеристики пласта и др.

Следует заметить, что все аналитические решения о притоке к горизонтальной скважине являются приближёнными. Одни авторы рассматривают горизонтальную скважину как линию стоков, другие, в лучшем варианте, как вертикальную трещину, высотой равной диаметру скважину. Что касается плотности расхода на единицу потока, то все аналитические решения построены в предположении одинаковой плотности (расхода на единицу длины горизонтального ствола). Известны также работы [2,4,5], авторы которых предполагали два явно отличных временных периода при дренировании пласта – начальный период с круговым радиальным притоком к поверхности ствола в вертикальной плоскости и поздний период с горизонтальным и псевдорадиальным или линейным притоком. Однако, как отмечают некоторые исследователи [3 и др.], первый период является малым по сравнению с общим сроком эксплуатации скважины. При этом, допущение о радиальном (псевдорадиальном) притоке к линейному стоку во втором периоде может трактоваться как адекватный процесс притока к неограниченному по протяжённости горизонтальному стволу. Но если скважина дренирует ограниченный пласт, то эквипотенциали не могут быть правильными по форме окружностями или эллипсами. В этом случае поле линий тока и поле эквипотенциалей становятся более сложными. Супрунович и Батлер [3] рассматривают задачу оптимизации размеров площади дренирования (сетку скважин) в зависимости от площади и длины и горизонтального ствола в следующей постановке. Предполагается псевдостационарный поток в двухмерной модели. Площадь нефтеносности пласта разбивается на ряд прямоугольников одинаковой формы, в центре которой симметрично сторон и располагается горизонтальная скважина длиной (рисунок 1).

Вследствие симметрии рассмотрение задачи ограничивается четвертью площади дренирования и отыскивается оптимальная сетка размещения скважин (оптимальное соотношение длины и ширины прямоугольной площади дренирования), позволяющая получать наибольший дебит скважины.

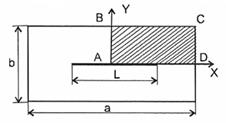
Рис. 1. Схема прямоугольной площади дренирования с центральным расположением горизонтального ствола

При этом решается плоская задача притока к горизонтальной скважине, описываемого уравнением

(1)

при граничных условиях, когда градиенты давления по нормали к сторонам прямоугольника равны нулю ( при и при ), т. е. границы прямоугольника принимаются непроницаемыми.

Поскольку ни на подошве, ни на кровле граничные условия не задаются, то авторы [3], строго говоря, решают плоскую задачу в режиме истощения залежи, принимая единичную толщину пласта () в качестве вертикальной трещины, а в последствии при определении дебита трещины и горизонтального ствола учитывают как толщину пласта, так и конвергенцию вертикального потока.

В уравнении (1) приняты следующие обозначения: – дебит скважины, – коэффициент вязкости, – коэффициент проницаемости пласта по горизонтали, – площадь дренирования, – депрессия на пласт, – пластовое давление, – среднее давление на контуре скважины.

Приводя уравнение (1) к безразмерному виду и заменяя его системой конечно-разностных уравнений с использованием пентадиагональной матрицы блока и способа решения, изложенного в книге А. Сеттери и К. Азиза [1], Р. Супрунович и Р. Батлер получили следующую приближённую формулу для расчёта наибольшего дебита горизонтального ствола и вертикальной трещины ГРП единичной высоты, соответствующего оптимальным размерам площади дренирования в форме прямоугольника.

(2)

где – безразмерный параметр (функция фильтрационного сопротивления) определяется асимптотическим выражением

при . (3)

При заданных параметрах и оптимальные размеры прямоугольника определяются по формулам:

; . (4)

Итак, в двухмерном пласте горизонтальная скважина рассматривается как линия стока, а в трёхмерном пространстве как вертикальная трещина. При этом предполагается, что форма сетки размещения горизонтального ствола остаётся той же самой.

В соответствии с формулой Дюпюи параметр для вертикальной скважины через площадь дренирования выразится как

(5)

а эффективность вертикальной трещины определяется кратностью отношения

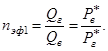(6)

Приток к горизонтальному стволу в трёхмерном пространстве подобен притоку к вертикальной трещине, но линии тока при этом должны конвергировать к поверхности скважины, вызывая дополнительное падение давления на преодоление фильтрационного сопротивления, как для вертикальной трещины. Чтобы избежать трудности при непосредственном решении этой задачи численным способом, авторы [3] использовали известную аппроксимацию, предложенную Ю. П. Борисовым. В соответствии с этим было найдено выражение для падения давления за счёт вертикальной конвергенции

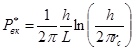, (7)

где

– толщина пласта.

Теперь дебит горизонтальной скважины будет определяться формулой

. (8)

Для однородно-анизотропного пласта в формулу (7) надо ввести коэффициент анизотропии , т. е. Вместо принять:

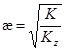; , (9)

где и – соответственно коэффициенты проницаемости по горизонтали и вертикали пласта.

Эффективность горизонтальной скважины по отношению к вертикальной скважине составит

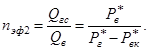(10)

Эффективность вертикальной трещины по отношению к горизонтальной скважине выражается соотношением

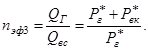(11)

Пример. Приняв исходные параметры: æ=3,3; 15м площади дренирования 8; 16; 32; 64 га; длину горизонтальной скважины 500; 200м, требуется рассчитать оптимальные размеры и сетки размещения горизонтальных стволов, вертикальных трещин и сравнительную их эффективность.

Расчёты, произведённые по формулам (3) - (7), (10) и (11), представлены в таблице 1. На рисунке 2 показано изменение эффективности работы горизонтальной скважины по сравнению с вертикальной в зависимости от длины и площади дренирования .

Из графиков и таблицы видно, что с уменьшением площади дренирования и увеличением протяжённости скважины эффективность возрастает. Так при плотности сетки 8 га с размером прямоугольника 575 и 139 м, что соответствует условному эквивалентному радиусу дренирования 160 м для вертикальной скважины, увеличение дебита для горизонтальной скважины составляет почти 13 раз, а для вертикальной трещины 51 раза, и для вертикальной трещины по сравнению с горизонтальной скважиной 4 раза.

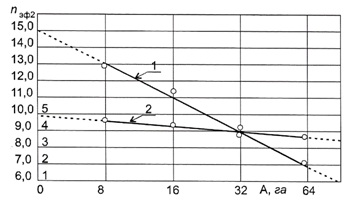
Рис. 2. Изменение эффективности работы горизонтальной скважины по сравнению с вертикальной (м; м)

Таблица 1

Результаты расчёта оптимальных размеров сетки размещения горизонтальных стволов и вертикальных трещин и их эффективность при исходных параметрах ,

Примечание:

– эффективность трещины разрыва по отношению к вертикальной скважине;

– эффективность горизонтального ствола по отношению к вертикальному;

– эффективность трещины разрыва по отношению к горизонтальной скважине.

Следует отметить, что сравнительная оценка эффективности горизонтальной скважины и вертикальной трещины одинаковой длины произведена сугубо на теоретической основе в предположении, что следует из постановки задачи – “нулевой” ширины трещины. Для реальной трещины эффективность очевидно существенно возрастёт.

На рисунке 3 представлена сравнительная оценка эффективной работы трещины разрыва и горизонтальной скважины по отношению к вертикальной скважине при параметре , выражающим удельную площадь дренирования.

Заметим также, что приведённая методика не рассматривает рациональное размещение горизонтальной скважины относительно ВНК или ГНК. Эта задача рассмотрена в работе [6].

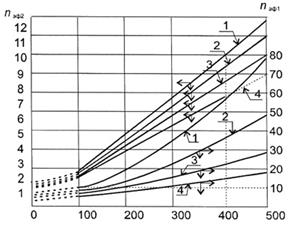
Рис. 3. Изменение эффективности работы трещин разрыва и горизонтальной скважины по сравнению с вертикальной при параметре А (га): 1-8, 2-16, 3-32, 4-64.

Выводы

- Разработанная методика определения оптимальных размеров сетки размещения горизонтальных скважин приемлема доля практических расчётов и может быть использована для оценки эффективности использования горизонтальных скважин и в другой постановке решения задач (см. размеры и в таблице 1);

- Эффективность работы горизонтальной скважины и вертикальной трещины возрастает с увеличением их протяжённости и уменьшением площади дренирования (уплотнения сетки скважин);

- Линейная зависимость соотношений дебитов при фиксированных значениях длины горизонтального ствола даёт возможность прогнозировать эффективность работы горизонтальной скважины для различных значений площади дренирования ;

- Приведённые формулы для расчёта дебитов соответствуют режиму истощения замкнутой залежи; для других условий следует использовать соответствующие формулы, вытекающие из постановки задач.

Рецензенты:

Грачев С.И., д.т.н., профессор, заведующий кафедрой «Разработка и эксплуатация нефтяных и газовых месторождений», Институт геологии и нефтегазодобычи, ФГБОУ ВПО ТюмГНГУ, г. Тюмень;

Леонтьев С.А., д.т.н., профессор, профессор кафедры «Разработка и эксплуатация нефтяных и газовых месторождений», Институт геологии и нефтегазодобычи, ФГБОУ ВПО ТюмГНГУ, г. Тюмень.

Библиографическая ссылка