Одной из наиболее актуальных задач имитационного моделирования эргатических систем является определение передаточных функций объекта и оператора. Однако возможность решения этой задачи ограничивается действием в целостной системе организмического принципа (исключается возможность непосредственной параметрической идентификации; возможно лишь последовательное уточнение параметров итеративным методом). При работах по созданию тренажных и обучающих комплексов для подготовки операторов различных транспортных систем [1,6,7] выяснилось, что эффективным способом решения задач параметрической идентификации является использование инженерных методов аппроксимации корреляционных функций (позволяют определить приближенные аналитические выражения спектральной плотности). Здесь корреляционная функция представляется в виде кусочно-линейной функции (алгебраическая сумма типовых треугольных корреляционных функций). Каждая типовая корреляционная функция определяется двумя параметрами - ![]() и
и ![]() . Имеем:
. Имеем:
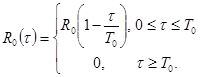
Отметим, ![]() . Каждой типовой треугольной корреляционной функции
. Каждой типовой треугольной корреляционной функции ![]() соответствует спектральная плотность
соответствует спектральная плотность
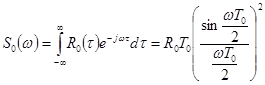 .
.
Введя 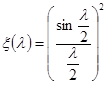 , получим
, получим ![]() .
.
Если ![]() с достаточной степенью точности аппроксимируется алгебраической суммой
с достаточной степенью точности аппроксимируется алгебраической суммой ![]() типовых треугольных корреляционных функций
типовых треугольных корреляционных функций ![]() , то:
, то:
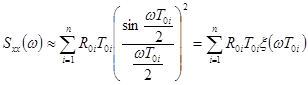 .
.
Точность определения спектральной плотности тем выше, чем меньше расхождение между корреляционными функциями: действительной и результирующей аппроксимированной. При этом несоответствие в значениях функции для малых ![]() будет преимущественно вызывать отклонение в значениях спектральной плотности при больших
будет преимущественно вызывать отклонение в значениях спектральной плотности при больших ![]() .
.
Взаимная спектральная плотность ![]() в общем случае является комплексной величиной:
в общем случае является комплексной величиной:
![]() ;
;
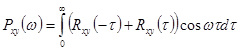 ,
, 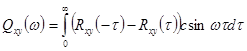
(![]() - четная функция, а
- четная функция, а ![]() - нечетная).
- нечетная).
Введя ![]() ,
, ![]()
(![]()
![]()
![]()
![]()
![]() ),
),
получим
![]() =
=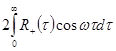 ,
, ![]() =
=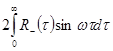 . (1)
. (1)
В силу четности ![]() ее можно рассматривать как некоторую корреляционную функцию. Сравнивая далее выражение (1) для
ее можно рассматривать как некоторую корреляционную функцию. Сравнивая далее выражение (1) для ![]() с формулой
с формулой
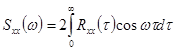 ,
,
видим, что они по форме совпадают. Следовательно, для вычисления ![]() по
по ![]() можно воспользоваться одним из методов приближенного вычисления спектральной плотности, которые рассмотрели ранее.
можно воспользоваться одним из методов приближенного вычисления спектральной плотности, которые рассмотрели ранее.
Рассмотрим методы приближенного вычисления мнимой части взаимной спектральной плотности (аппроксимация корреляционной функции ![]() типовыми корреляционными функциями): метод типовых треугольных и метод типовых экспоненциальных корреляционных функций.
типовыми корреляционными функциями): метод типовых треугольных и метод типовых экспоненциальных корреляционных функций.
Сначала рассмотрим метод типовых треугольных корреляционных функций. Наиболее удобно и просто ![]() аппроксимировать кусочно-линейной функцией. Тогда в качестве типовых корреляционных функций могут быть взяты треугольные корреляционные функции. При этом функция
аппроксимировать кусочно-линейной функцией. Тогда в качестве типовых корреляционных функций могут быть взяты треугольные корреляционные функции. При этом функция ![]() приближенно представляется в виде алгебраической суммы какого-либо числа типовых треугольных корреляционных функций. Мнимая часть
приближенно представляется в виде алгебраической суммы какого-либо числа типовых треугольных корреляционных функций. Мнимая часть ![]() взаимной спектральной плотности будет также приближенно представляться в виде алгебраической суммы функций от
взаимной спектральной плотности будет также приближенно представляться в виде алгебраической суммы функций от ![]() , соответствующих типовым треугольным функциям.
, соответствующих типовым треугольным функциям.
Если, как и ранее типовую треугольную функцию обозначить ![]() , то:
, то:
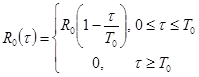
введя функцию ![]() , определяемую формулой, аналогичной (1), получим:
, определяемую формулой, аналогичной (1), получим:
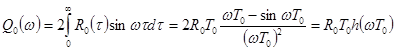 ,
, ![]() .
.
Если ![]() , то
, то
![]() .
.
Метод экспоненциальных корреляционных функций аналогичен методу типовых экспоненциальных корреляционных функций, использованному для аппроксимации корреляционных функций. Для положительных ![]() функция
функция ![]() представляется в виде суммы типовых экспоненциальных корреляционных функций
представляется в виде суммы типовых экспоненциальных корреляционных функций
![]() ,
,
где ![]() – некоторые коэффициенты,
– некоторые коэффициенты, ![]() ;
; ![]() – целые числа.
– целые числа.
Заметим, так как ![]() , то
, то ![]() . Все формулы, полученные ранее для вычисления
. Все формулы, полученные ранее для вычисления ![]() , остаются в силе. Получим:
, остаются в силе. Получим:
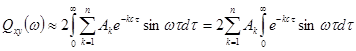
или
![]() .
.
В силу того, что полученная таким образом ![]() есть нечетная функция, то эта формула пригодна для вычисления
есть нечетная функция, то эта формула пригодна для вычисления ![]() при
при ![]() .
.
Таким образом, алгоритм решения уравнения идентификации в частотной области сводится к последовательному выполнению указанных ниже процедур.
1.Вычисление дискретных значений автокорреляционной функции
![]() ,
,
где интервал реализации ![]() , шаг по времени
, шаг по времени ![]() , интервал корреляции
, интервал корреляции ![]() связаны соотношениями:
связаны соотношениями:
![]() ;
; ![]() ;
; ![]() .
.
2. Построение графика ![]() .
.
3. Кусочно-линейная аппроксимация графика ![]() .
.
4. Построение графиков типовых треугольных корреляционных функций; определение ![]() и
и ![]() .
.
5. Вычисление
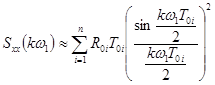 ,
, ![]() .
.
6. Вычисление дискретных значений взаимной корреляционной функции
![]() .
.
7. Вычисление
![]() .
.
8. Построение графика ![]() .
.
9. Кусочно-линейная аппроксимация графика ![]() .
.
10. Построение графиков типовых треугольных корреляционных функций; определение
![]() и
и ![]() .
.
11. Вычисление
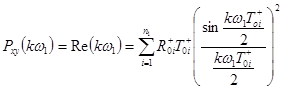 .
.
12. Вычисление
![]() .
.
13. Построение графика ![]() .
.
14. Кусочно-линейная аппроксимация графика ![]() .
.
15. Построение графиков типовых треугольных корреляционных функций; определение ![]() и
и ![]() .
.
16. Вычисление
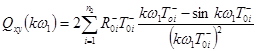 .
.
17. Вычисление вещественной частотной характеристики
![]() .
.
18. Вычисление мнимой частотной характеристики
![]() .
.
19. Вычисление амплитудной частотной характеристики
![]() .
.
20. Вычисление фазовой частотной характеристики
![]() .
.
21. Аппроксимация амплитудной частотной характеристики типовыми звеньями.
22. Построение фазовой характеристики.
Предложенный алгоритм использовался при построении когнитивной модели управляющих воздействий оператора в эргатической системе [2…5].
Рецензенты:
Родионов Ю.В., д.т.н., профессор, декан автомобильно-дорожного института ПГУАС, заведующий кафедрой «Эксплуатация автомобильного транспорта», г. Пенза;
Логанина В.И., д.т.н., профессор, зав. кафедрой «Управление качеством и технологии строительного производства» Пензенского государственного университета архитектуры и строительства, г. Пенза.
Библиографическая ссылка
Гарькина И.А., Данилов А.М., Сухов Я.И. АЛГОРИТМ РЕШЕНИЯ УРАВНЕНИЯ ИДЕНТИФИКАЦИИ В ЧАСТОТНОЙ ОБЛАСТИ ПО ТИПОВЫМ ТРЕУГОЛЬНЫМ КОРРЕЛЯЦИОННЫМ ФУНКЦИЯМ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=19647 (дата обращения: 13.02.2026).



