Современный уровень развития промышленных объектов, таких как производство этилена и пропилена, требует комплексного подхода при использовании методов и средств автоматического контроля и управления параметров технологических процессов [1].
В настоящее время подавляющее большинство контуров функционирует в сложных структурах систем регулирования, которые содержат перекрестные связи в объекте регулирования. Настройки каждого контура существенно зависят от характеристик других контуров, в том числе от параметров настройки регуляторов в этих контурах.
В том случае, если в многомерной системе неправильно настроен один контур, чаще всего это проявляется в появлении периодических колебаний одной частоты с разными амплитудами и фазами во всех взаимодействующих контурах. Предопределить такой контур с регулятором, который часто называют корневым контуром, является весьма трудной задачей. Кроме того, в современных условиях эксплуатации автоматизированных систем управления технологическим процессом инженер, занимающийся настройкой регуляторов, отвечает за несколько сотен контуров регулирования. Попытки устранения возникающих в системе предаварийных ситуаций приведут только к простым приемам, заключающимся в ослаблении настройки регуляторов. При этом будет снижаться качество работы системы, однако функционирование процесса в таких условиях допустимо [2].
Итак, можно заключить, что настройка таких систем является довольно сложной задачей, а для того, чтобы получить параметры модели, рекомендуется нанести возмущение выбранной формы регулирующим органом при отключенном регуляторе и записать переходный процесс.
Следовательно, для того чтобы получить параметры настройки, необходимо организовать и провести на действующих промышленных установках эксперимент с выводом объекта из нормального режима работы на довольно длительное время, что может привести к невосполнимым экономическим затратам для предприятия.
Применение нечетких логических систем в различных отраслях промышленности является высокоэффективным направлением развития современных предприятий, при этом не заменяя обычной техники управления, а дополняя ее методологией реализации стратегий многосвязного управления [3].
Таким образом, предлагается повысить качество систем регулирования путем использования оптимальных нелинейных управляющих устройств, которые изменяют параметры настройки регуляторов в зависимости от значений регулируемой переменной и позиционера регулирующего органа. При этом модель объекта описывается линейным уравнением.
Исходя из вышесказанного, поставим задачу реализации и исследования различных систем управления, а именно:
1) одноконтурная система управления с ПИ-регулятором;
2) каскадная система управления с основным и вспомогательным регуляторами;
3) система управления на базе нечеткой логики.
В качестве объекта регулирования выбрали поддержание уровня конденсата в вертикальном трубчатом испарителе узла дистилляции производства полиэтилена высокой плотности.
Кроме того, для реализации системы управления предлагается использовать промышленный контроллер UDC 2500 компании Honeywell. Рассматриваемый программируемый контроллер обладает объемом памяти программы 12 шагов, а также возможностью использования алгоритмов нечеткой логики.
Структурная схема моделей вышеобозначенных систем управления, выполненная в программном комплексе Matlab, изображена на рисунке 1.
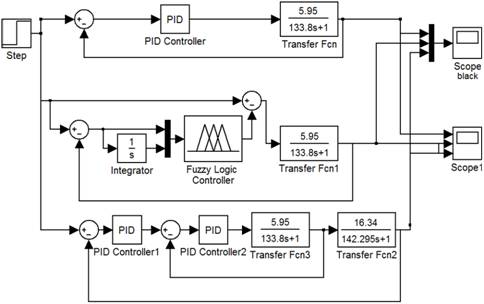
Рис. 1. Структурная схема одноконтурной, каскадной систем управления и система управления с ПИ-подобным нечетким регулятором
Проектирование регуляторов для объектов управления проводили в интерактивной системе для анализа линейных и нелинейных динамических систем Simulink. Данная система является надстройкой программного продукта MatLab и представляет собой графическую среду имитационного моделирования, позволяющую при помощи блок-диаграмм в виде направленных графов строить динамические модели, включая дискретные, непрерывные и гибридные, нелинейные и разрывные системы.
В случае одноконтурной и каскадной систем управления были определены параметры регулирования, обеспечивающие регулирование выходной величины объекта с требуемой точностью.
Система управления с нечетким регулятором выполнена при помощи алгоритма Мамдани на основе пяти правил. Данный алгоритм описывает несколько последовательно выполняющихся этапов. При этом каждый последующий этап получает на вход значения, полученные на предыдущем шаге:
1) формирование базы правил;
2) фаззификация;
3) активация подзаключений;
4) агрегирование подусловий;
5) аккумулирование заключений;
6) дефаззификация.
Кроме того, ввели две входные переменные «X1» и «X2» и выходную переменную «Out» и построили функции принадлежности для термов используемых переменных (рис. 2).
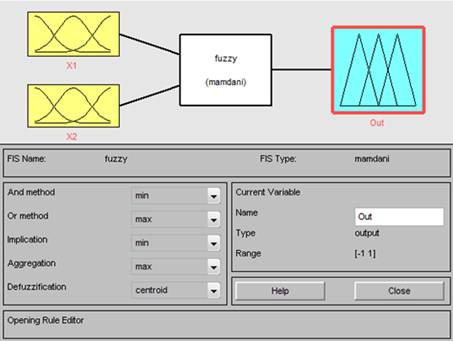
Рис. 2. Входные и выходные переменные нечеткого регулятора
При настройке нечеткого регулятора воспользовались правилами, которые приведены в таблице 1.
Таблица 1
Правила настройки нечеткого регулятора
|
№ |
Правило нечеткого регулятора |
|
1 |
Если (X1 = okay), то (Out = Z) |
|
2 |
Если (X1 = low), то (Out = LP) |
|
3 |
Если (X1 = high), то (Out = LN) |
|
4 |
Если (X1 = okay) и (X2 = positive), то (Out = SP) |
|
5 |
Если (X1 = okay) и (X2 = negative), то (Out = SN) |
После этого сформировали обозначенные правила в блоке настройки правил пакета FuzzyLogic (рис. 3).
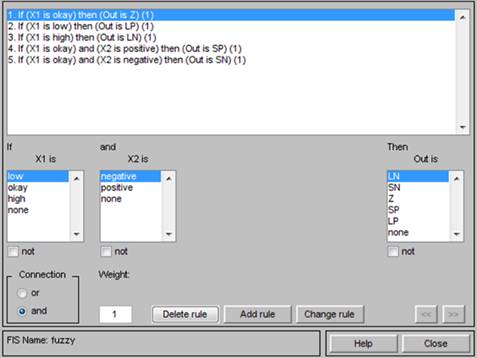
Рис. 3. Блок настройки правил
Экспортировав настройки регулятора в рабочее пространство программной среды MatLab и указав данные настройки в помещенном в окне Simulink регуляторе, получили систему управления с нечетким регулятором.
На следующем этапе необходимо сравнить качество регулирования спроектированных систем управления. Для этого требуется получить кривые переходного процесса посредством подачи на них ступенчатого воздействия. В программной среде Simulink данную функцию выполняет блок «Step».
Кроме того, для удобства графического представления переходных процессов изобразили их в одной координатной плоскости, использовав при этом мультиплексор «Mux», и в разных. В качестве приемника сигналов использовали осциллограф «Scope», который позволяет строить графики исследуемых сигналов в функции во времени [5].
Так, подав единичное ступенчатое воздействие на одноконтурную, каскадную систему и систему с нечетким регулятором, получили изображенные на рисунке 4 графики переходных процессов.
1 – одноконтурная автоматическая система регулирования; 2 – каскадная система регулирования; 3 – система регулирования с ПИ-подобным нечетким регулятором
Рис. 4. Графики переходных процессов
Анализ переходных процессов произвели по основным прямым показателям качества. Полученные показатели свели в таблицу 2.
Таблица 2
Прямые показатели качества переходных процессов
|
Показатель качества |
Одноконтурная система регулирования |
Каскадная система регулирования |
Система регулирования с нечетким регулятором |
|
Статическая ошибка |
0 |
0 |
0,016 |
|
Время регулирования |
9,5 |
4,5 |
3,9 |
|
Перерегулирование |
0,349 |
0,176 |
0 |
|
Степень затухания |
0,865 |
1 |
1 |
Таким образом, было определено, что подбором типов и форм функций принадлежности можно также улучшить и качество управления при использовании нечеткого регулятора в системе автоматического управления.
В результате получившихся показателей качества получили, что система управления с нечетким регулятором в отличие от одноконтурной и каскадной системы при применении к исследуемому объекту обладает нулевым перерегулированием и меньшим временем регулирования. Однако управление при помощи нечеткого логического аппарата характеризуется наличием небольшой статической ошибки по сравнению с классическими аналоговыми системами управления, а также с системами управления на базе нейронных сетей и статистических методов [3, 4].
Рецензенты:
Баширов М.Г., д.т.н., профессор, заведующий кафедрой ЭАПП филиала ФГБОУ ВПО УГНТУ, г. Салават;
Жирнов Б.С., д.х.н., профессор, заведующий кафедрой ХТП филиала ФГБОУ ВПО УГНТУ, г. Салават.
Библиографическая ссылка
Вильданов Р.Г., Панфилов В.В., Аслаев Р.Р. ИССЛЕДОВАНИЕ И РЕАЛИЗАЦИЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ НА ОСНОВЕ НЕЧЕТКОЙ ЛОГИКИ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=19590 (дата обращения: 12.03.2026).



