Как отмечено авторами в работах [1, 9, 12], кинематические параметры являются одной из составляющих группы параметров механизмов любого вида, оказывающих непосредственное влияние на работоспособность приводов технологического оборудования. Процесс модернизации и развития промышленного потенциала РФ в условиях импортозамещения выводит на первый план потребность формирования приводов технологического оборудования на базе механизмов, обладающих достаточно простой структурой, образованной минимально возможным числом подвижных звеньев и кинематических пар. Техническим объектам с перечисленными свойствами соответствуют механизмы с замкнутой системой тел качения (ЗСТК). Механизмы данного вида обладают структурой, образованной совокупностью двух колец с дорожками качения, замкнутой системой тел качения с диаметрами равной или разной величины и сепаратором (водило). Тела качения могут обладать гладкими рабочими поверхностями (фрикционные) [1, 3-12] или поверхностями с выступами (зубчатые) [2]. Наличие сепаратора в структуре механизмов с ЗСТК позволяет исключить контакт тел качения друг с другом, обеспечив между ними наличие зазора. Передача движения между звеньями в этом случае осуществляется посредством непосредственного контакта тел качения с дорожками качения обоих колец.
Коллектив авторов проводит исследования геометрических, кинематических и силовых параметров приводов технологического оборудования, разработанных на базе эпициклических механизмов с ЗСТК с диаметрами разной (эксцентриковые) [1, 2, 5, 8, 9, 11, 12] или равной (соосные) [3, 4, 6, 7, 10, 12] величины. В ходе исследований установлено: структуры механизмов данного вида содержат замкнутые системы тел качения, следовательно, задача определения номинальных величин геометрических параметров механизмов должна решаться при начальных условиях, что исходные параметры являются постоянными величинами больше нуля при наличии или отсутствии зазора между телами качения [1, 5, 8, 12]. Однако дальнейшие исследования показали, что для решения задачи по определению номинальных величин геометрических параметров при данных условиях необходим ввод поправки в расчет, считая один из исходных параметров величиной переменной. Вариация значениями радиуса тел качения и зазора не позволяет достичь требуемого результата. В этом случае получаем, что решение задачи имеет два возможных направления ввода поправки, либо по радиусу дорожки качения наружного кольца, либо по радиусу дорожки качения внутреннего кольца. Это обстоятельство необходимо учитывать также при определении скоростей скольжения, оказывающих непосредственное влияние на передаточные отношения механизмов данного вида. В работах [1, 9, 12] авторами предложен алгоритм решения поставленной задачи при ведущем наружном кольце и вводе поправки в расчет номинальных величин геометрических параметров по радиусу дорожки качения этого же звена. Однако ранее было выявлено, что задача по определению номинальных величин геометрических параметров механизмов с ЗСТК имеет два направления ввода поправки. Это означает, что для более полного выявления свойств механизмов данного вида необходимо реализовать анализ влияния направления ввода поправки на величины скоростей скольжения точек контакта звеньев механизмов с ЗСТК.
Настоящее исследование проводится с целью совершенствования алгоритма определения скоростей скольжения точек контакта звеньев эпициклических механизмов с ЗСТК с диаметрами разной величины для любого вида симметричной структурной схемы при ведущем наружном кольце и обоих направлений ввода поправки в расчет номинальных величин геометрических параметров. Это дает возможность выполнить анализ влияния направления ввода поправки на величины скоростей скольжения точек контакта звеньев механизмов данного вида. Полученные результаты позволят формировать привода технологического оборудования на базе планетарных механизмов с замкнутой системой тел качения, обладающих требуемыми свойствами и кинематическими параметрами.
Методы исследования, применяемые в настоящей работе, основаны на принципах кинематического анализа эпициклических механизмов при использовании положений геометрии и тригонометрии.
Рассмотрим пример определения величин скоростей скольжения точек контакта i-ого тела качения с дорожками качения обоих колец механизма с ЗСТК с диаметрами разной величины для обоих направлений ввода поправки в расчет номинальных величин геометрических параметров. Для этого составим расчетную модель (рис. 1) и примем следующие исходные условия и обозначения: наружное кольцо является ведущим звеном, сепаратор выступает в качестве выходного звена, внутреннее кольцо остановлено; ![]() ,
, ![]() – дорожки качения внутреннего и наружного колец; RВ, RН, ОВ и OН – радиусы и геометрические центра дорожек качения внутреннего и наружного колец; e – эксцентриситет; С – сепаратор (водило);
– дорожки качения внутреннего и наружного колец; RВ, RН, ОВ и OН – радиусы и геометрические центра дорожек качения внутреннего и наружного колец; e – эксцентриситет; С – сепаратор (водило); ![]() – зазор между телами качения; r0, r1, ri, 0, 1, i и
– зазор между телами качения; r0, r1, ri, 0, 1, i и ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() – радиусы, геометрические центра и точки контакта максимального, первого и i-ого тел качения с дорожками качения наружного и внутреннего колец; XВ OВ YВ – неподвижная система координат жестко связанная с внутренним кольцом; XН OВ YН, Xi i Yi и XВi iВ YВi – подвижные системы координат жестко связанные с наружным кольцом и i-ым телом качения;
– радиусы, геометрические центра и точки контакта максимального, первого и i-ого тел качения с дорожками качения наружного и внутреннего колец; XВ OВ YВ – неподвижная система координат жестко связанная с внутренним кольцом; XН OВ YН, Xi i Yi и XВi iВ YВi – подвижные системы координат жестко связанные с наружным кольцом и i-ым телом качения; ![]() – угловая координата наружного кольца в неподвижной системе координат XВ OВ YВ;
– угловая координата наружного кольца в неподвижной системе координат XВ OВ YВ; ![]() и
и ![]() – угловые координаты точки i-ого тела качения в подвижных системах координат Xi i Yi; и XВi iВ YВi.
– угловые координаты точки i-ого тела качения в подвижных системах координат Xi i Yi; и XВi iВ YВi.
Анализ расчетной модели механизма с ЗСТК при рассматриваемых условиях показывает, что двойная точка контакта i-ого тела качения с дорожкой качения наружного кольца образована совпадением точек ![]() и
и ![]() расположенных на поверхностях обоих контактирующих звеньев, которые в статическом состоянии механизма с ЗСТК совпадают. При движении звеньев точки
расположенных на поверхностях обоих контактирующих звеньев, которые в статическом состоянии механизма с ЗСТК совпадают. При движении звеньев точки ![]() и
и ![]() будут перемещаться с разными линейными скоростями. В этом случае положение точки
будут перемещаться с разными линейными скоростями. В этом случае положение точки ![]() , принадлежащей дорожке качения наружного кольца в подвижной системе координат XН OВ YН, определяется при помощи радиус-вектора
, принадлежащей дорожке качения наружного кольца в подвижной системе координат XН OВ YН, определяется при помощи радиус-вектора
![]() (1)
(1)
где ![]() – матрица поворота дорожки качения наружного кольца с угловой координатой
– матрица поворота дорожки качения наружного кольца с угловой координатой ![]() ;
; ![]() – радиус-вектор определяющий положение точки
– радиус-вектор определяющий положение точки ![]() принадлежащей дорожке качения наружного кольца в неподвижной системы координат XВ OВ YВ [9].
принадлежащей дорожке качения наружного кольца в неподвижной системы координат XВ OВ YВ [9].
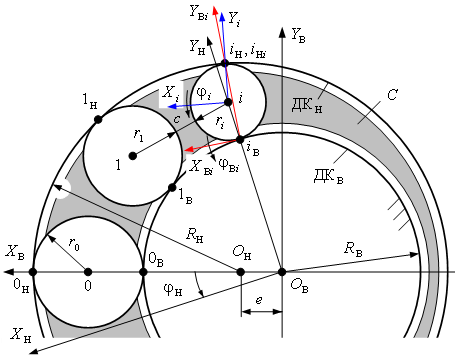
Рис. 1. Расчетная модель механизма с замкнутой системой тел качения с диаметрами разной величины при ведущем наружном кольце
Абсолютное движение точки ![]() принадлежащей i-ому телу качения разложим на два составляющих движения. Первым является относительное вращательное движение вокруг оси, проходящей через его центр c угловой координатой
принадлежащей i-ому телу качения разложим на два составляющих движения. Первым является относительное вращательное движение вокруг оси, проходящей через его центр c угловой координатой ![]() . Вторым является вращательное движение центра i-ого тела качения вокруг оси, проходящей через мгновенный центр скоростей (точки
. Вторым является вращательное движение центра i-ого тела качения вокруг оси, проходящей через мгновенный центр скоростей (точки ![]() ) с угловой координатой
) с угловой координатой ![]() . Тогда положение точки
. Тогда положение точки ![]() принадлежащей i-ому телу качения в подвижной системе координат XН OВ YН , определяется при помощи радиус-вектора
принадлежащей i-ому телу качения в подвижной системе координат XН OВ YН , определяется при помощи радиус-вектора
![]() (2)
(2)
где ![]() и
и ![]() – матрицы поворота i-ого тела качения относительно
– матрицы поворота i-ого тела качения относительно
точек ![]() и
и ![]() .
.
Абсолютное скольжение в зоне контакта i-ого тела качения с дорожкой качения наружного кольца определим как
![]() (3)
(3)
Следуя работе [9], подставим (1) и (2) в равенство (3) и выполним ряд преобразований. В результате получим формулу для определения скоростей скольжения точек контакта звеньев механизмов с ЗСТК
![]() (4)
(4)
Слагаемые, содержащиеся в формуле (4), определяются посредством решения системы параметрических уравнений, имеющей следующий вид
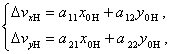 (5)
(5)
где
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
По формуле (4) с учетом выражений (5-9) выполнен расчет величин скоростей скольжения точек контакта тел качения с дорожкой качения наружного кольца механизма с ЗСТК с диаметрами разной величины для всех видов симметричных структурных схем с учетом обоих направлений ввода поправки. При вычислениях считаем, что RН = 100 мм, RВ = 50 мм, е = 6 мм, с = 6 мм, угловая скорость наружного кольца ?Н = 50 с-1. С целью повышения эффективности процесса вычислений авторами разработано программное обеспечение в виде программного комплекса «Эксцентрик», зарегистрированного в Реестре программ для ЭВМ Федеральной службы по интеллектуальной собственности Российской Федерации (РОСПАТЕНТ № 2012614197). По полученным результатам построены диаграммы скоростей скольжения (рис. 2).
Анализ диаграмм (рис. 2) показывает, что независимо от вида симметричных структурных схем и направления ввода поправки в расчет номинальных величин геометрических параметров механизмов с ЗСТК рост значений радиусов тел качения приводит к снижению величин скоростей скольжения. Различия в видах кривых скоростей скольжения объясняются особенностями состава структуры каждого вида механизма с ЗСТК. Так, вид кривых 1 соответствует наличию в структуре механизма на горизонтальной оси симметрии максимального и минимального тел качения. Особенность кривых 2 является следствием расположения на горизонтальной оси симметрии только максимального тела качения. Кривые скоростей скольжения 3 соответствуют наличию в структуре механизма с ЗСТК на горизонтальной оси симметрии только минимального тела качения, а для кривых 4 характерно отсутствие на горизонтальной оси симметрии и максимального, и минимального тел качения. При этом кривые 1 и 2, а также 3 и 4 имеют схожий вид независимо от направления ввода поправки.
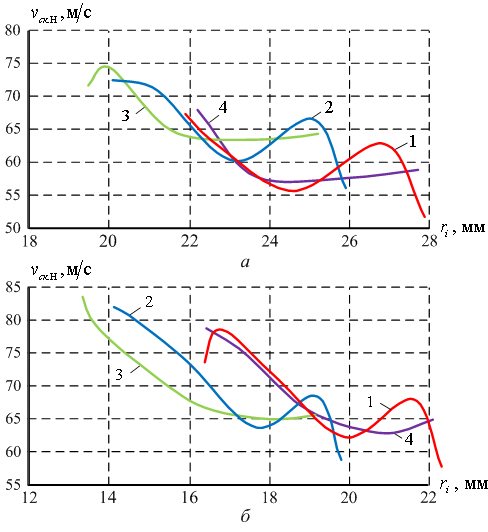
Рис. 2. Диаграммы скоростей скольжения точек контакта звеньев механизмов с ЗСТК с диаметрами разной величины
Ввод поправки в расчет по радиусу дорожки качения внутреннего кольца вызывает увеличение радиусов тел качения, что приводит к снижению величин скоростей скольжения двойных точек контакта (рис. 2, а). При вводе поправки по радиусу дорожки качения наружного кольца имеют место противоположные процессы, т. е. наблюдается рост значений скоростей скольжения (рис. 2, б) при схожем их количестве в структуре механизмов с ЗСТК. При принятых условий расчета минимально возможные значения скоростей скольжения имеют место для кривых 1, а максимально возможные значения скоростей скольжения соответствуют кривым 3 для любого направления ввода поправки.
Заключение. В результате получена формула для расчета величин скоростей скольжения точек контакта тел качения с дорожкой качения наружного кольца для любого вида симметричной структурной схемы механизма с замкнутой системой тел качения с диаметрами разной величины, а также установлены диапазоны их возможных значений и характер изменения в зависимости от направления ввода поправки. Выявлено, что ввод поправки в расчет номинальных величин геометрических параметров механизмов с ЗСТК по радиусу дорожки качения внутреннего кольца приводит к снижению величин скоростей скольжения точек контакта тел качения с дорожкой качения наружного кольца. Это позволяет формировать привода технологического оборудования на базе эпициклических механизмов с замкнутой системой тел качения, обладающих требуемыми свойствами и кинематическими параметрами.
Рецензенты:
Бронов С.А., д.т.н., доцент, профессор кафедры систем искусственного интеллекта, Институт космических и информационных технологий ФГАОУ ВПО «Сибирский федеральный университет», Красноярск;
Носков М.В., д.ф-м.н., профессор, Институт космических и информационных технологий ФГАОУ ВПО «Сибирский федеральный университет», г. Красноярск.
Библиографическая ссылка
Мерко М.А., Меснянкин М.В., Мерко И.С., Колотов А.В., Митяев А.Е., Кайзер Ю.Ф., Лысянников А.В., Лысянникова Н.Н., Белякова С.А., Литвинов П.С. ВЛИЯНИЕ НАПРАВЛЕНИЯ ВВОДА ПОПРАВКИ НА ВЕЛИЧИНЫ СКОРОСТЕЙ СКОЛЬЖЕНИЯ ТОЧЕК КОНТАКТА ЗВЕНЬЕВ МЕХАНИЗМОВ С ЗСТК С ДИАМЕТРАМИ РАЗНОЙ ВЕЛИЧИНЫ ПРИ ВЕДУЩЕМ НАРУЖНОМ КОЛЬЦЕ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=19569 (дата обращения: 13.02.2026).



