Современное развитие техники и технологии заставляет разработчиков гидросистем применять жидкости с характеристиками, отличающимися по реологическим свойствам от ньютоновских жидкостей для обеспечения более широких возможностей проектируемых изделий. При разработке гидропневмодемпферов находят применение специальные жидкости – магнитные и ферромагнитные рабочие жидкости (РЖ) [6]. Другим примером использования неньютоновских жидкостей служит нефтедобывающая отрасль промышленности, где в качестве основных рабочих жидкостей при добыче нефти служат псевдопластичные жидкости [2].
Определение потерь на трение в подобных задачах – важный вопрос, так как информация о потерях на трение дает возможность провести более точные расчеты характеристик создаваемой технической системы, а также снизить затраты, связанные с содержанием применяемой техники, и повысить ее ресурс.
В настоящее время для развития промышленности необходимо сформировать методику определения потерь на трение и местного сопротивления для неньютоновских жидкостей. Задачу определения потерь на трение по длине для псевдопластичных жидкостей в гладкой круглой трубе необходимо решить в первую очередь. Ряд зарубежных исследований также связаны с изучением подобной задачи [6, с. 3-5].
Работа по исследованию реологических свойств жидкостей является частью НИР № Э34 от 30 апреля 2014 г., выполняемой в настоящее время.
Данная статья посвящена составлению и проверке методики определения потерь на трение в гидравлически гладкой круглой трубе (т.е. когда шероховатость стенки не оказывает влияния на характер движения и потери на трение по длине трубы [5]) для псевдопластичных жидкостей и ее анализу. В рамках данной статьи также рассмотрен способ анализа характеристик рабочих жидкостей, применяемых буровых растворов, для верификации полученной методики.
1. Характеристика рабочих жидкостей
Многообразие моделей жидкости, встречающихся в практической деятельности человека, представлено на рис. 1 [8], где они разбиты по характерному признаку – закону, связывающему касательное напряжение, возникающее в жидкости, и скорость деформации сдвига.
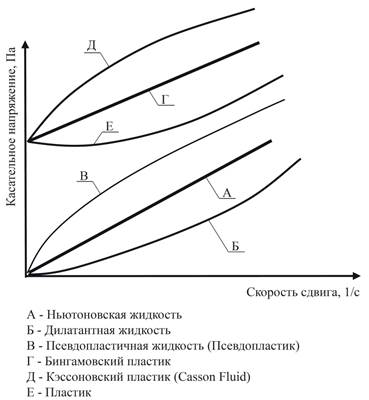
Рис. 1. Графики, отражающие свойства жидкости.
Примеры жидкостей приведены в таблице 1.
Таблица 1
Тип жидкости
|
Тип кривой |
Пример жидкости |
|
А |
Вода, масла (гидравлическое, моторное и др.) |
|
Б |
Растворы сахара и крахмалы |
|
В |
Большинство продуктов питания, глины, жидкий цемент и буровые растворы |
|
Г |
Продукты питания, содержащие высокий уровень жиров (сливочное масло, маргарин, шоколад, майонез и др.) |
|
Д |
Жидкости, содержащие твердые частицы (расплавленный шоколад и кровь) |
|
Е |
Пластики |
Графические зависимости (рис. 1) определяет аналитическое выражение [3; 4]
![]() (1)
(1)
В уравнении (1): ![]() – касательное напряжение; для кривых «А», «Б» и «В»
– касательное напряжение; для кривых «А», «Б» и «В»![]() = 0 – предел текучести при скорости сдвига, равной 0;
= 0 – предел текучести при скорости сдвига, равной 0; ![]() – мера консистенции жидкости;
– мера консистенции жидкости; ![]() – скорость сдвига; n – характеризует степень неньютоновского поведения материала от поведения ньютоновской жидкости [4; 5].
– скорость сдвига; n – характеризует степень неньютоновского поведения материала от поведения ньютоновской жидкости [4; 5].
Соотношение (1) представляет собой обобщенный реологический закон.
Для ньютоновских жидкостей (рис. 1, зависимость «А») уравнение (1) принимает вид
![]() (2)
(2)
В уравнении (2): μ – коэффициент динамической вязкости; Y – расстояние, измеряемое от центра трубы в направлении стенки; u – значение скорости на расстоянии Y; ![]() – скорость сдвига; t – время; lx – длина пути в направлении скорости движения u [4; 5].
– скорость сдвига; t – время; lx – длина пути в направлении скорости движения u [4; 5].
В качестве рабочей жидкости при исследовании был взят раствор (линейный гель), применяемый на практике псевдопластичной жидкости с характеристиками, которые были установлены экспериментально.
2. Определение параметров исследуемой жидкости
Для исследуемой псевдопластичной жидкости было проведено измерение параметра кажущейся динамической вязкости (далее вязкости). Измерение вязкости производилось с помощью прибора – реометра Fann 35 [9].
Реометр позволяет проводить полномасштабные исследования реологических свойств среды с низкой вязкостью при высоких скоростях сдвига.
Вид экспериментальных характеристик исследуемой жидкости приведен на рис. 2, 3. Экспериментальные зависимости были найдены при температуре окружающей среды (температуре жидкости), равной 23 °С. Более подробно методика по определению параметров исследуемой жидкости будет представлена в последующих статьях.
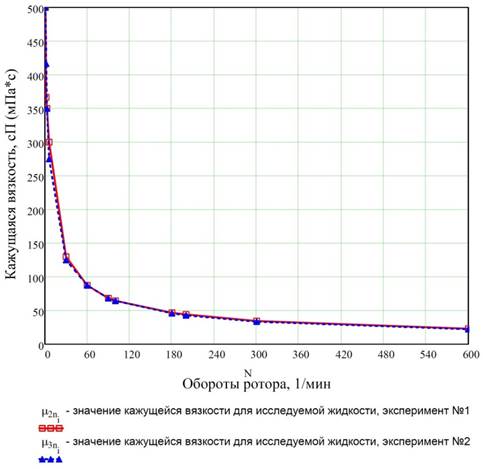 а
а
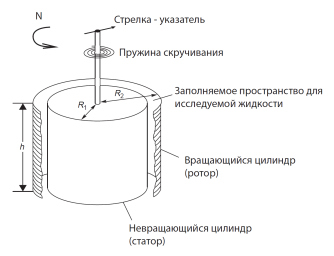 б
б
Рис. 2: а – характеристика исследуемой жидкости. Зависимость: «Кажущаяся вязкость – обороты вращения ротора-вискозиметра»; б – принципиальная схема соосно - цилиндрического вискозиметра.
Между ротором и статором пространство заполняется исследуемой жидкостью. Подробный расчет прибора и режимов его работы по определению реологических свойств жидкости будет приведен в последующих статьях (работах).
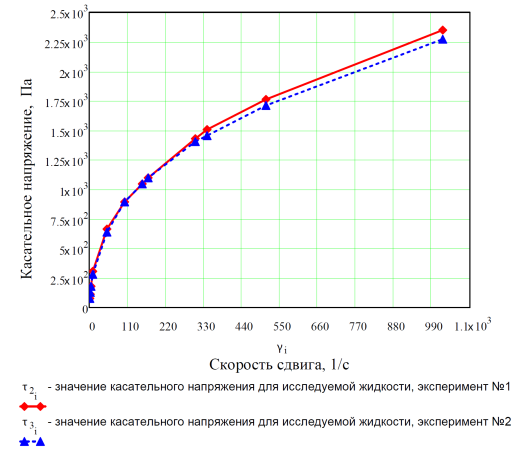
Рис. 3. Характеристика исследуемой жидкости. Зависимость: «Касательное напряжение – скорость сдвига».
Полученные с помощью прибора значения кажущейся вязкости![]() , коэффициентов
, коэффициентов ![]() и
и ![]() [9] используются в созданной методике.
[9] используются в созданной методике.
Коэффициенты n и k были подобраны по графику рис. 3, используя соотношение (1), так, коэффициент n=0,415, а коэффициент k=2,596 Па![]() сn.
сn.
Найденные значения необходимо ввести в качестве исходных данных при моделировании течения псевдопластичной жидкости в программе ANSYS.
3. Составление математической модели
Согласно [5], при турбулентном течении рабочей жидкости в трубах профиль скорости описывается степенным законом
![]() (3)
(3)
где s – показатель, зависящий от числа Рейнольдса [5]; R – внутренний радиус проходного сечения трубы; Y – расстояние, измеряемое от центра трубы в направлении стенки; u – значение скорости на расстоянии Y; U – максимальная скорость жидкости.
Значение средней скорости жидкости определяется по следующему выражению:
![]() ,
,
где Q – расход рабочей жидкости, А – площадь проходного сечения канала трубы.
Если представить отношение средней скорости ![]() к максимальной U, то получили
к максимальной U, то получили
![]()
(4)
Определяя максимальную скорость U из уравнения (4) и подставляя его в (3), и учитывая выражение для средней скорости ![]() , получили вид уравнения для профиля скорости в гладкой трубе:
, получили вид уравнения для профиля скорости в гладкой трубе:
![]()
В качестве предварительной оценки можно воспользоваться сведениями для изучения характеристик неньютоновских жидкостей согласно [3; 4; 7; 8].
Согласно [3; 4; 8] и [7], интегральная зависимость для потери давления по длине – ![]() , как функция коэффициента сопротивления трения cf, для гладкой круглой трубы для неньютоновских жидкостей определяется выражением
, как функция коэффициента сопротивления трения cf, для гладкой круглой трубы для неньютоновских жидкостей определяется выражением
где L – длина участка трубы, на котором определяется потеря давления на трении; D ‑ внутренний диаметр проходного сечения трубы, D = 2R; ρ – плотность жидкости.
Обобщенное число Рейнольдса [3; 4]:
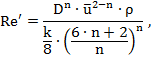 (7)
(7)
является весьма удобным для нахождения перепада давлений в трубе. Для всех неньютоновских жидкостей применяют обобщенное число Рейнольдса в качестве оценки турбулизации потока, которое учитывает реологические свойства исследуемой жидкости.
В соотношении (7): n =![]() , а k =
, а k = ![]()
В свою очередь, для определения коэффициента ![]() необходимо воспользоваться соотношением вида [5]:
необходимо воспользоваться соотношением вида [5]:
![]() (8)
(8)
где a и b являются функциями ![]() и определяются по таблице 2.
и определяются по таблице 2.
Реологические параметры жидкости ![]() и
и ![]() - близки по смыслу к n и k [3; 4].
- близки по смыслу к n и k [3; 4].![]() – показатель консистенции жидкости и характеризует степень разжиженности материала (чем выше k’, тем более вязкой является жидкость),
– показатель консистенции жидкости и характеризует степень разжиженности материала (чем выше k’, тем более вязкой является жидкость), ![]() – показатель, характеризующий отклонение физических свойств материала от поведения ньютоновской жидкости – показатель поведения жидкости. Чем сильнее отличие
– показатель, характеризующий отклонение физических свойств материала от поведения ньютоновской жидкости – показатель поведения жидкости. Чем сильнее отличие ![]() от 1 (больше единицы для дилатановских жидкостей и меньше единицы для псевдопластиков), тем с большим основанием можно рассматривать данную жидкость как неньютоновскую [3; 4].
от 1 (больше единицы для дилатановских жидкостей и меньше единицы для псевдопластиков), тем с большим основанием можно рассматривать данную жидкость как неньютоновскую [3; 4].
Таблица 2
Зависимость коэффициентов a и b в уравнении (8) от числа ![]()
|
|
a |
b |
|
0,2 |
0,0646 |
0,349 |
|
0,3 |
0,0685 |
0,325 |
|
0,4 |
0,0712 |
0,307 |
|
0,6 |
0,0740 |
0,281 |
|
0,8 |
0,0761 |
0,263 |
|
1,0 |
0,0779 |
0,250 |
|
1,4 |
0,0804 |
0,231 |
|
2,0 |
0,0826 |
0,213 |
Применяя интерполяцию значений параметров a и b таблицы 2, получили функции для их определения в зависимости от любого значения параметра n’. Для определения интерполяционных зависимостей параметров a и b воспользовались стандартными функциями программы MathCAD, вид которых следующий:
![]()
![]()
![]()
![]()
где ![]() ,
, ![]() – векторы коэффициентов для построения аппроксимирующего полинома второй степени, требуемого функцией interp; 0,65 – параметр, определяющий размер отрезков полинома аппроксимирующей функции. Было выбрано минимальное значение, при котором возможна аппроксимация. Данный параметр задает степень сглаженности данных.
– векторы коэффициентов для построения аппроксимирующего полинома второй степени, требуемого функцией interp; 0,65 – параметр, определяющий размер отрезков полинома аппроксимирующей функции. Было выбрано минимальное значение, при котором возможна аппроксимация. Данный параметр задает степень сглаженности данных. ![]() или
или ![]() , определяемые через функцию interp – функцию интерполирования в точке x по исходным векторам
, определяемые через функцию interp – функцию интерполирования в точке x по исходным векторам ![]() или
или ![]() и коэффициентам сплайна
и коэффициентам сплайна ![]() или
или ![]() , соответственно.
, соответственно. ![]() – интерполяционная зависимость для ряда значений «a», таблица 2, а
– интерполяционная зависимость для ряда значений «a», таблица 2, а ![]() – интерполяционная зависимость для ряда значений «b», таблица 2.
– интерполяционная зависимость для ряда значений «b», таблица 2.
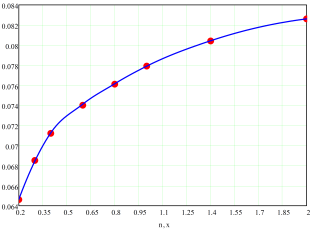
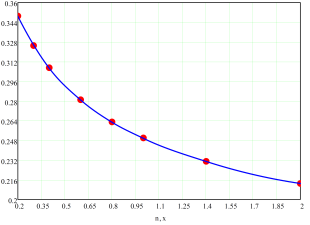
Зависимости функций ![]() и
и ![]() приведены на рис. 4.
приведены на рис. 4.
 а
а
 б
б
Рис. 4: а – интерполяция коэффициента «а» таблицы 2; б – интерполяция коэффициента «b» таблицы 2.
Коэффициент ![]() можно также определить по графику зависимости
можно также определить по графику зависимости ![]() , приведенному на рис. 5 [4; 7].
, приведенному на рис. 5 [4; 7].
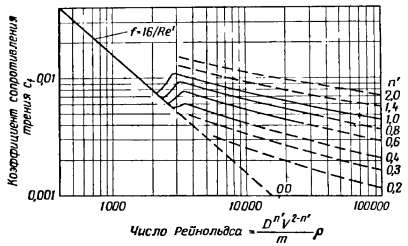
Рис. 5. График зависимости коэффициента сопротивления трения cf для ламинарного и турбулентного течений неньютоновских жидкостей.
___ – области опытных значений;
- - - – области экстраполированных значений.
m – знаменатель в выражении (7).
Применяя первый способ определения коэффициента сопротивления трения cf (аналитический способ определения коэффициента сопротивления трения cf), получили значение потери давления по длине ![]() . При втором способе определения коэффициента cf (графический способ определения коэффициента сопротивления трения cf) получили
. При втором способе определения коэффициента cf (графический способ определения коэффициента сопротивления трения cf) получили ![]() .
.
Для определения потерь, вызванных гидравлическим сопротивлением по длине, и верификации результатов для разных рабочих жидкостей была создана численная модель. Ее создание включает в себя следующие этапы.
1. Построение модели канала трубы в программе Pro/Engineer и ее передача в среду ANSYS.
2. Создание «сетки» для модели канала экспериментальной трубы [1; 10]. Метод построения «сетки»: MultiZone; тип «сетки»: Hexa; количество слоев: 10, «сгущение» слоев задано неравномерным, густота сдвинута к стенке для учета погрешности слоев.
Результат приведен на рис. 6.
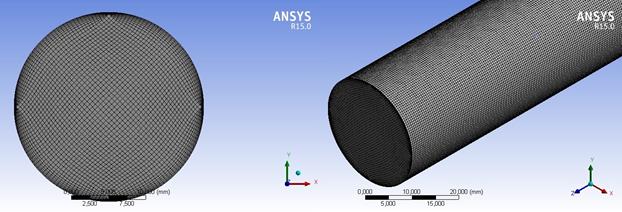
Рис. 6. «Сетка» для модели канала экспериментальной трубы.
Для криволинейных, и в частности для цилиндрических, поверхностей рекомендуется применять сетку типа O-Grid, т.е. сетку в виде совокупности блоков, которая выстраивает линии в виде буквы «О». При помощи данной сетки повышается качество элементов, расположенных на непрерывной кривой или поверхности [1].
С помощью метода построения MultiZone производится операция построения топологии на геометрии, затем в автоматическом режиме строится поверхностная блочная структура трубы. Далее поверхностные блоки преобразуются в объемные. Полученная структура обладает очень важным свойством параметризации. В любой момент можно изменить параметры гексаэдрической сетки вокруг объекта и перестроить ее, поэтому данный метод очень удобен для решения задач [1; 10].
Для определения величины размера сетки воспользовались следующими соотношениями [1]. Из выражения для безразмерного расстояния от стенки трубы определили размерное расстояние от стенки трубы [1]
![]()
где ![]() - безразмерное расстояние от стенки трубы [1], приняли равным 30,
- безразмерное расстояние от стенки трубы [1], приняли равным 30, ![]() – эквивалентный коэффициент динамической вязкости,
– эквивалентный коэффициент динамической вязкости, ![]() – плотность жидкости.
– плотность жидкости.
![]() – динамическая скорость, определяемая по следующему соотношению [1; 3]
– динамическая скорость, определяемая по следующему соотношению [1; 3]
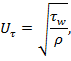
где ![]() – касательное напряжение на стенке, вычисляемое по зависимости [1]
– касательное напряжение на стенке, вычисляемое по зависимости [1]
![]()
![]() – определили по соотношению (8).
– определили по соотношению (8).
Эквивалентный коэффициент динамической вязкости ![]() определили из соотношения
определили из соотношения
![]()
Используя приведенные соотношения, определили величину ![]() . Величину размера ячейки сетки назначали равной 0,5 мм с учетом сделанных выше оценочных расчетов.
. Величину размера ячейки сетки назначали равной 0,5 мм с учетом сделанных выше оценочных расчетов.
Для решения задачи течения жидкости в круглой цилиндрической трубе, был построен профиль скорости на «входе» в трубу.
Теоретическую зависимость профиля скорости (5) ввели в качестве начального условия в программу ANSYS, FLUENT. Для этого был написан программный код на языке С++, используемый в программе ANSYS [12].
Выбрали модель течения рабочей жидкости ![]() . Уравнения движения преобразуются к виду, в котором добавлено влияние флуктуации средней скорости (в виде турбулентной кинетической энергии) и процесса уменьшения этой флуктуации за счёт изменения скорости диссипации турбулизации энергии. Данная модель позволяет учитывать течение в погранслое [11; 13].
. Уравнения движения преобразуются к виду, в котором добавлено влияние флуктуации средней скорости (в виде турбулентной кинетической энергии) и процесса уменьшения этой флуктуации за счёт изменения скорости диссипации турбулизации энергии. Данная модель позволяет учитывать течение в погранслое [11; 13].
Применяя зависимость (5) и параметры течения рабочей жидкости, получили профиль скорости, представленный на рис. 7.
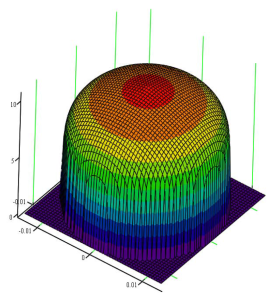 а
а
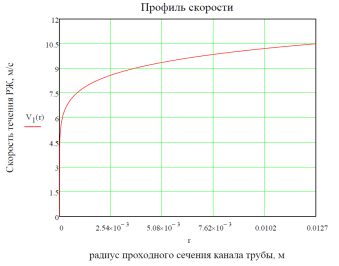 б
б
Рис. 7. Теоретический профиль скорости:
а – в пространстве; б – в плоскости сечения.
Для профиля скорости, приведенного на рис. 7 и описанного выражением (5), коэффициент s получили равным ![]() Данный коэффициент подбирался в результате численного моделирования с помощью нескольких итераций, чтобы получить минимальную ошибку в распределении профиля скорости по сечению трубы.
Данный коэффициент подбирался в результате численного моделирования с помощью нескольких итераций, чтобы получить минимальную ошибку в распределении профиля скорости по сечению трубы.
4. Экспериментальное определение коэффициента сопротивления гидравлического трения по длине трубы
Коэффициент сопротивления трения cf может быть определен экспериментальным путем либо по численному эксперименту, результаты которого приведены на рис. 10, либо по натурному эксперименту. В любом случае необходимо установить связь между потерями давления по длине – ![]() и геометрией канала. Коэффициент сопротивления трения cf также связан с коэффициентом потерь на трение по длине λ следующим соотношением
и геометрией канала. Коэффициент сопротивления трения cf также связан с коэффициентом потерь на трение по длине λ следующим соотношением
![]()
Таким образом, экспериментально коэффициент сопротивления трения cf определяется зависимостью
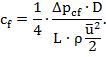 (9)
(9)
На рис. 8 представлено графическое изображение универсального закона сопротивления для гладкой трубы, т.е. когда шероховатость стенки не оказывает влияния на характер движения и потери на трение по длине трубы [5], что соответствует прикладному характеру работы, связанному с нефтегазовой и нефтедобывающей отраслью промышленности. Кривая (1) соответствует закону Прандтля, кривая (2) – закону Блазиуса.
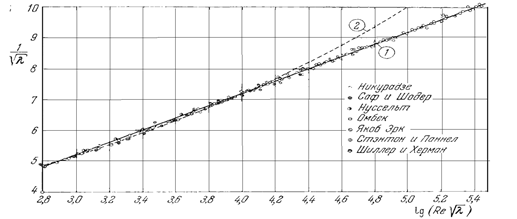
Рис. 8. Универсальный закон сопротивления для гладкой трубы
1 – закон Прандтля; 2 – закон Блазиуса.
5. Результаты численного эксперимента
Полученные результаты приведены на рис. 9, 10.
Течение осуществляется слева направо. Входное сечение – левый торец трубы. Контрольные сечения расположены вдоль канала через 541 мм.
Начало координат помещено в геометрический центр расчётной области. Ось Z направлена вдоль оси трубы. X, Y, соответственно перпендикулярно Z. Координата Z=0 находится правее на расстоянии 1082 мм от входного сечения. По оси ординат откладывается расстояние от оси трубы. Внутренний диаметр трубы 25,4 мм.
На графике потерь давления на гидравлическое трение по длине (рис. 10) по оси абсцисс откладывается расстояние по оси Z трубы от левого торца к правому. По оси ординат - величина падения давления.
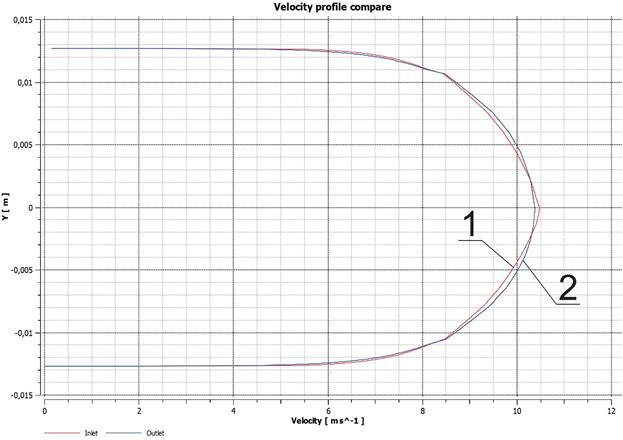
Рис. 9. Профиль скорости для исследуемой жидкости (псевдопластичная жидкость).
Ось X - значение скорости, м/с; Ось Y - радиус трубы, м.
1 – предполагаемый профиль скорости (аналитическая модель);
2 – профиль скорости исследуемой жидкости (численный эксперимент).
Максимальная относительная погрешность полученного профиля скорости от предполагаемого профиля скорости может быть оценена величиной
![]() (10)
(10)
где ![]() – значения скорости в зависимости от Y - текущего расстояния от центра трубы до стенки для предполагаемого профиля скорости (рис. 9, кривая 1);
– значения скорости в зависимости от Y - текущего расстояния от центра трубы до стенки для предполагаемого профиля скорости (рис. 9, кривая 1);
![]() – значения скорости в зависимости от Y для профиля скорости исследуемой жидкости (рис. 9, кривая 2) – численный результат.
– значения скорости в зависимости от Y для профиля скорости исследуемой жидкости (рис. 9, кривая 2) – численный результат.
Согласно выражению (10) ∆max = 0,962%.
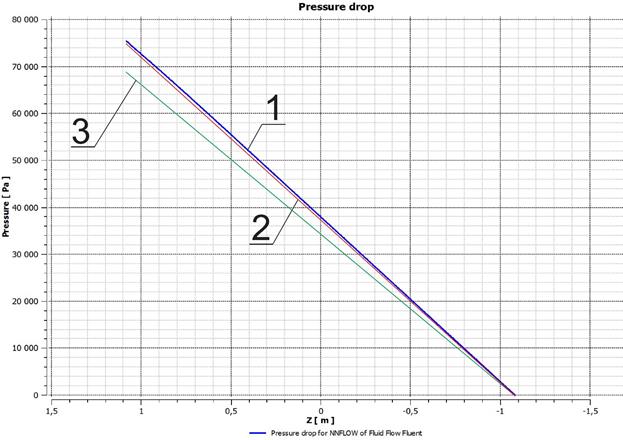
Рис. 10. Потери давления на гидравлическое трение по длине.
Ось Z - длина, м; Ось Y - потеря давления, Па.
1 – зависимость для исследуемой жидкости (псевдопластичной) – численный эксперимент;
2 – зависимость для исследуемой жидкости (аналитический способ определения коэффициента сопротивления трения cf);
3 – зависимость для исследуемой жидкости (графический способ определения коэффициента сопротивления трения cf).
Максимальная относительная погрешность полученной зависимости потерь на гидравлическое трение по длине от предполагаемой зависимости может быть оценена:
![]() (11)
(11)
где ![]() – величина потерь на гидравлическое трение по длине для псевдопластичной жидкости при численном эксперименте (рис. 10, кривая 1);
– величина потерь на гидравлическое трение по длине для псевдопластичной жидкости при численном эксперименте (рис. 10, кривая 1);
![]() – величина потерь на гидравлическое трение по длине, аналитическая модель (рис. 10, кривая 2).
– величина потерь на гидравлическое трение по длине, аналитическая модель (рис. 10, кривая 2).
Согласно выражению (11) ∆max = 9,868%.
Однако если оценить погрешность для кривой 1 и 2 рис. 10 по зависимости (11), то она составит ∆ = 0,526%.
Заключение
Научной новизной работы является решение актуальной задачи, имеющей существенное значение для отрасли машиностроения, а именно: создана методика определения потерь на гидравлическое трение для круглой гладкой цилиндрической трубы, которую в дальнейшем можно изменять для оптимизации задачи по определению энергозатрат и затрат, связанных с содержанием парка техники и оборудования, а также оптимальных режимов работы техники.
Получена методика определения потерь на трение в гидравлически гладкой круглой трубе для псевдопластичной жидкости.
Результаты работы состоят в следующем.
1. Создана методика, позволяющая рассчитать потери по длине, вызванные гидравлическим сопротивлением для гладкой цилиндрической трубы при течении для псевопластичной жидкости, с использованием экспериментальных данных.
2. Определены реологические параметры используемой при буровых работах жидкости.
3. Получена величина потерь на гидравлическое трение по длине круглой цилиндрической трубы для псевдопластичной жидкости и определен коэффициент сопротивления трения cf.
4. Проверена и подтверждена зависимость вида (5) для распределения профиля скорости по сечению круглой цилиндрической трубы для псевдопластичной жидкости при турбулентном режиме течения и подобран показатель степени в указанной зависимости распределения профиля скорости.
На основании проведенного анализа могут быть сделаны следующие выводы.
1. В результате сравнения численного эксперимента и предложенной аналитической модели для определения профиля скорости в гладкой круглой трубе для певдопластичной жидкости относительная ошибка составляет ![]() 1,0%.
1,0%.
2. Расчет показал, что полученные результаты численного эксперимента и аналитических зависимостей по определению величины потерь на трение по длине совпадают с максимальной погрешностью до 9,9% (для графического определения коэффициента сопротивления трения cf), и могут быть приняты для анализа и определения потерь по длине для псевдопластичных жидкостей. Предложенный аналитический способ определения коэффициента сопротивления трения cf приводит к максимальной погрешности величины потерь на трение по длине, равной 0,5%.
3. Определив потери давления по длине, можно дать рекомендации по потребляемой мощности в системе, а также спрогнозировать ресурс и уменьшить затраты для обеспечения работоспособности оборудования.
4. Полученные характеристики, приведенные на рис. 9, 10, позволяют определять коэффициент сопротивления трения cf.
Работа выполняется в рамках контракта по НИР № Э34 от 30 апреля 2014 г. Коллектив авторов выражает благодарность за оказанную помощь в написании и оформлении статьи Сафоновой С.Е.
Рецензенты:
Грехов Л.В., д.т.н., профессор, профессор кафедры «Поршневые двигатели», ФГБОУ ВПО «Московский государственный технический университет имени Н.Э. Баумана», г. Москва;
Сорокин Ф.Д., д.т.н., доцент, профессор кафедры прикладной механики, ФГБОУ ВПО «Московский государственный технический университет имени Н.Э. Баумана», г. Москва.
Библиографическая ссылка
Рябинин М.В., Труханов К.А. МЕТОДИКА ОПРЕДЕЛЕНИЯ ПОТЕРЬ НА ТРЕНИЕ В ГИДРАВЛИЧЕСКИ ГЛАДКОЙ КРУГЛОЙ ТРУБЕ ДЛЯ ПСЕВДОПЛАСТИЧНЫХ ЖИДКОСТЕЙ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=19505 (дата обращения: 16.02.2026).



