Одной из актуальных задач современной навигации беспилотных летательных аппаратов (БПЛА) является задача повышения точности определения координат. Эта задача решается путём использования различных вариантов комплексирования навигационных систем. Одним из современных вариантов комплексирования является сочетание gps/глонасс-навигации с расширенным фильтром Калмана (Extended Kalmanfilter), рекурсивно оценивающего точность с помощью неполных и зашумленных измерений. В данный момент существуют и разрабатываются различные вариации расширенного фильтра Калмана, включающие разнообразное число переменных состояний [4]. В этой работе мы покажем, насколько эффективным может быть его использование в современных разработках. Рассмотрим одно из характерных представлений подобного фильтра [5].
Построение математической модели
В данном примере мы будем говорить только о движении БПЛА в горизонтальной плоскости, иначе, мы рассмотрим так называемую проблему 2d локализации [2]. В нашем случае это оправдано тем, что для многих практически встречающихся ситуаций БПЛА может оставаться примерно на одной и той же высоте. Это предположение широко используется для упрощения моделирования динамики летательных аппаратов [2]. Динамическая модель БПЛА задается следующей системой уравнений:
![]()
![]()
![]() (1)
(1)
![]()
![]()
где {![]() } – координаты БПЛА в горизонтальной плоскости как функции времени,
} – координаты БПЛА в горизонтальной плоскости как функции времени, ![]() направление БПЛА,
направление БПЛА, ![]() угловая скорость БПЛА, и v
угловая скорость БПЛА, и v![]() путевая скорость БПЛА, функции
путевая скорость БПЛА, функции ![]() и
и ![]() будем считать постоянными. Они взаимно независимы, с известными ковариациями
будем считать постоянными. Они взаимно независимы, с известными ковариациями![]() и
и ![]() , равными
, равными![]() и
и ![]() соответственно и используются для моделирования изменений ускорения БПЛА, вызванных ветром, маневрами пилота и т.д. Значения
соответственно и используются для моделирования изменений ускорения БПЛА, вызванных ветром, маневрами пилота и т.д. Значения ![]() и
и ![]() являются производными от максимальной угловой скорости БПЛА и опытных значений изменений линейной скорости БЛА,
являются производными от максимальной угловой скорости БПЛА и опытных значений изменений линейной скорости БЛА, ![]() – символ Кронекера.
– символ Кронекера.
Данная система уравнений будет приближенной из-за нелинейности в модели и из-за присутствия шума. Самый простой способ аппроксимации в данном случае – это приближение методом Эйлера. Дискретная модель динамической системы движения БПЛА показана ниже.
![]()
![]()
![]() (2)
(2)
![]()
![]()
![]() дискретный вектор состояний фильтра Калмана, позволяющий аппроксимировать значение непрерывного вектора состояний. ∆
дискретный вектор состояний фильтра Калмана, позволяющий аппроксимировать значение непрерывного вектора состояний. ∆![]() – временной интервал между k и k+1 измерениями. {
– временной интервал между k и k+1 измерениями. {![]() } и {
} и {![]() } – последовательности значений белого гауссовского шума с нулевым средним значением. Матрица ковариации для первой последовательности:
} – последовательности значений белого гауссовского шума с нулевым средним значением. Матрица ковариации для первой последовательности:
E{![]() } =
} = ![]() ∆
∆![]()
Аналогично, для второй последовательности:
E{![]() } =
} = ![]() ∆
∆![]()
Выполнив соответствующие замены в уравнениях системы (2), получаем:
![]()
![]()
Последовательности ![]() и
и ![]() взаимно независимы. Они также являются последовательностями белого гауссовского шума с нулевым средним значением и с матрицами ковариации
взаимно независимы. Они также являются последовательностями белого гауссовского шума с нулевым средним значением и с матрицами ковариации ![]() и
и ![]() соответственно. Преимущество этой формы в том, что она показывает изменение дискретного шума в интервале между каждыми измерениями. В итоге получаем следующую дискретную динамическую модель:
соответственно. Преимущество этой формы в том, что она показывает изменение дискретного шума в интервале между каждыми измерениями. В итоге получаем следующую дискретную динамическую модель:
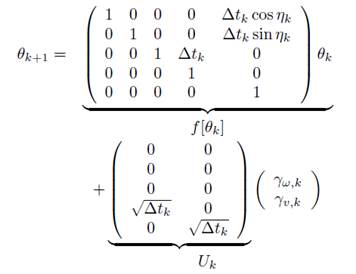 (3)
(3)
Уравнение для ![]() :
:
![]() =
= ![]() +
+ ![]() , (4)
, (4)
где, х и y – координаты БПЛА в k-момент времени, а ![]() гауссовская последовательность случайных параметров с нулевым средним значением, которая используется для задания погрешности. Предполагается, что эта последовательность не зависит от {
гауссовская последовательность случайных параметров с нулевым средним значением, которая используется для задания погрешности. Предполагается, что эта последовательность не зависит от {![]() } и {
} и {![]() }.
}.
Выражения (3) и (4) служат основой для оценки местоположения БПЛА, где к-е координаты получены с помощью расширенного фильтра Калмана. Моделлирование отказа навигационных систем применительно к данному типу фильтра показывает его существенную эффективность [5].
Для большей наглядности приведем небольшой простой пример. Пусть некоторый БПЛА летит равноускоренно, с некоторым постоянным ускорением а.
![]()
Где, х – координата БПЛА в t-момент времени, а δ – некоторая случайная величина.
Предположим, что у нас есть gps-сенсор, который получает данные о местоположении летательного аппарата. Представим результат моделирования данного процесса в программном пакете MATLAB.
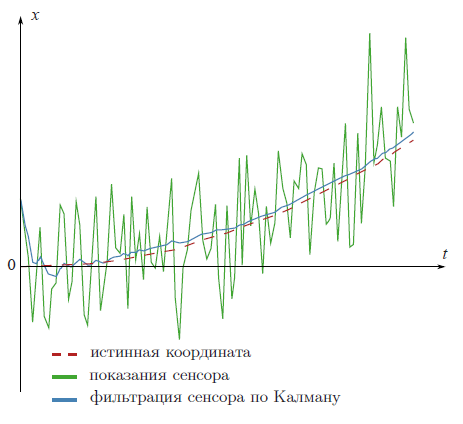
Рис. 1. Фильтрация показания сенсора с помощью фильтра Калмана
На рис. 1 видно, насколько эффективным может быть использование фильтрации по алгоритму Калмана.
Однако в реальной ситуации сигналы зачастую имеют нелинейную динамику и ненормальный шум. Именно в таких случаях и используется расширенный фильтр Калмана. В том случае, если дисперсии шумов не слишком велики (т.е. линейная аппроксимация является адекватной), применение расширенного фильтра Калмана дает решение задачи с высокой точностью. Однако в том случае, когда шумы не являются гауссовскими, расширенный фильтр Калмана применять нельзя. В этом случае обычно применяют частичный фильтр, в котором используются численные методы взятия интегралов на основе методов Монте Карло с марковскими цепями.
Частичный фильтр
Представим один из алгоритмов, развивающих идеи расширенного фильтра Калмана – частичный фильтр. Частичная фильтрация является неоптимальным способом фильтрации, который работает при выполнении объединения методом Монте-Карло на множестве частиц, которые представляют собой распределение вероятностей процесса. Здесь частица это элемент, взятый из априорного распределения оцениваемого параметра. Основная идея частичного фильтра заключается в том, что большое количество частиц может быть использовано для представления оценки распределения. Чем большее число частиц используется, тем точнее множество частиц будет представлять априорное распределение. Фильтр частиц инициализируется помещением в него N частиц из априорного распределения параметров, которые мы хотим оценить. Алгоритм фильтрации предполагает прогон этих частиц через специальную систему, а затем взвешивание с помощью информации, полученной от измерения данных частиц. Полученные частицы и связанные с ними массы представляют апостериорное распределение оценочного процесса. Цикл повторяется для каждого нового измерения, и веса частиц обновляются для представления последующего распределения. Одна из основных проблем с традиционным подходом фильтрации частиц состоит в том, что в результате такой подход обычно имеет несколько частиц, имеющих очень большой вес, в отличие от большинства остальных, вес которых очень незначителен. Это приводит к нестабильности фильтрации [6]. Эта проблема может быть решена введением частоты дискретизации, где N новых частиц берется из распределения, составленного из старых частиц. Результат оценки получают путем получения выборки среднего значения множества частиц. Если мы имеем несколько независимых выборок, то средняя выборка будет точной оценкой среднего значения, задающей конечную дисперсию.
Даже если фильтр частиц является неоптимальным, то при стремлении количества частиц к бесконечности эффективность алгоритма приближается в байесову правилу оценивания. Поэтому желательно иметь столько частиц, сколько возможно, чтобы получить наилучший результат. К сожалению, это приводит к сильному увеличению сложности вычислений, а, следовательно, вынуждает к поиску компромисса между точностью и скоростью расчета. Итак, число частиц должно быть выбрано исходя из требований к задаче оценки точности. Еще одним важным фактором для работы фильтра частиц является ограничение на частоту дискретизации. Как упоминалось ранее, частота дискретизации является важным параметром фильтрации частиц и без него в конечном итоге алгоритм становится вырождающимся. Идея заключается в том, что если веса распределяются слишком неравномерно и порог дискретизации скоро будет достигнут, то частицы с низким весом отбрасываются, и оставшееся множество образует новую вероятностную плотность, для которой могут браться новые выборки. Выбор порога частоты дискретизации представляет собой довольно сложную задачу, ведь слишком высокая частота служит причиной чрезмерной чувствительности фильтра к шуму, а слишком низкая дает большую погрешность. Также важным фактором является плотность вероятности [6].
В целом, алгоритм фильтрации частиц показывает хорошую производительность расчета местоположения для стационарных целей и в случае относительно медленно движущихся целей с неизвестной динамикой ускорения. В общем случае, алгоритм фильтрации частиц является более стабильным, чем расширенный фильтр Калмана, и менее склонным к вырождению и серьезным сбоям. В случаях нелинейного, негауссового распределения данный алгоритм фильтрации показывает весьма хорошую точность определения местоположения цели, в то время как алгоритм расширенной фильтрации Калмана нельзя использовать при таких условиях. К минусам данного подхода можно отнести его более высокую сложность относительно расширенного фильтра Калмана, а также то, что не всегда очевидно, как правильно подобрать параметры для этого алгоритма.
Перспективные исследования в данной области
Использование модели фильтра Калмана, подобной той, что привели мы, можно видеть в [3], где он используется для улучшения характеристик комплексированной системы (GPS + модель компьютерного зрения для сопоставления с географической базой), и также моделируется ситуация отказа спутникового навигационного оборудования. С помощью фильтра Калмана результаты работы системы в случае отказа были существенно улучшены (например, погрешность в определении высоты была снижена примерно в два раза, а погрешности в определении координат по разным осям снижены практически в 9 раз). Аналогичное использование фильтра Калмана приведено также в [4].
Интересная с точки зрения совокупности методов задача решается в [1]. Там также используется фильтр Калмана с 5 состояниями, с некоторыми отличиями в построении модели. Полученный результат превосходит результат приведенной нами модели [5] за счет использования дополнительных средств комплексирования (используются фото и тепловизионные изображения). Применение фильтра Калмана в данном случае позволяет уменьшить погрешность определения пространственных координат заданной точки до значения 5,5 м.
Заключение
В заключение отметим, что использование фильтра Калмана в системах определения местоположения БПЛА практикуется во многих современных разработках. Существует огромное количество вариаций и аспектов такого использования, вплоть до одновременного применения нескольких подобных фильтров с разными факторами состояний [7]. Одним из наиболее перспективных направлений развития Калмановских фильтров видится работа над созданием модифицированного фильтра, погрешности которого будут представлены цветным шумом, что сделает его еще более ценным для решения реальных задач. Также большой интерес в данной области представляет собой частичный фильтр, с помощью которого можно фильтровать негауссовские шумы. Названное разнообразие и ощутимые результаты в повышении точности, особенно в случае отказа стандартных спутниковых навигационных систем, являются главными факторами влияния данной технологии на различные научные области, связанные с разработкой точных и отказоустойчивых навигационных систем для различных летательных аппаратов.
Рецензенты:
Лабунец В.Г., д.т.н., профессор, профессор кафедры теоретических основ радиотехники Уральского федерального университета имени первого Президента России Б.Н. Ельцина, г. Екатеринбург;
Иванов В.Э., д.т.н., профессор, зав. кафедрой технологии и средств связи Уральского федерального университета имени первого Президента России Б.Н. Ельцина, г. Екатеринбург.
Библиографическая ссылка
Гаврилов А.В. ИСПОЛЬЗОВАНИЕ ФИЛЬТРА КАЛМАНА ДЛЯ РЕШЕНИЯ ЗАДАЧ УТОЧНЕНИЯ КООРДИНАТ БПЛА // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=19453 (дата обращения: 01.02.2026).



