При компьютерном моделировании процессов растворения и диффузии газов в оксидных стеклах основная проблема заключается в создании адекватной молекулярной модели самой матрицы (стекла), которая корректно отражала бы не только структуру ближнего порядка, но и топологию межузельного пространства, где собственно и происходят указанные процессы. По сути дела речь идет о «правильных» пространственных упаковках базовых структурных элементов матрицы, определяющих так называемый средний порядок (т. е. структурные особенности с масштабом от нескольких ангстрем до нанометра). В случае систем на основе кремнезема такими структурными элементами являются кремнийкислородные тетраэдры. В центре каждого тетраэдра находится атом кремния. Сами же тетраэдры соединяются друг с другом при помощи атомов так называемого мостикового кислорода, находящихся в вершинах тетраэдров. Следовательно, каждый атом мостикового кислорода разделен соответствующими парами атомов кремния. В результате образуется пространственная сеть кремнийкислородных тетраэдров, соединенных друг с другом вершинами. Для иллюстрации на рисунке 1 показано стереоизображение фрагмента одной из моделей кварцевого стекла, полученной в рамках данной работы (стереопара перекрестная).
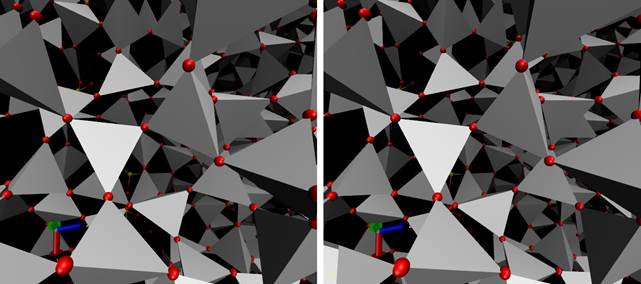
Рис. 1. Фрагмент пространственной сети кремнийкислородных тетраэдров. Красные сферы в вершинах тетраэдров — мостиковый кислород
К настоящему времени сформировались два основных подхода к созданию молекулярных моделей стекол. Первый заключается в формировании нерегулярной пространственной сетки за счет случайных перестановок связей в исходной регулярной (кристаллической) структуре. Учет Максвелл—Больцмановского фактора при перестановке связей привел к разработке эффективного алгоритма (WWW), который позволил получить довольно реалистичные модели аморфного кремния и германия [10]. При помощи модифицированного алгоритма WWW были также построены и исследованы модели кварцевого стекла, содержащие до 300 тыс. атомов [9]. Статистические свойства этих моделей очень хорошие — они бездефектны, имеют узкие функции радиальных и угловых распределений. Но, к сожалению, такие алгоритмы (по сути это варианты методов Монте-Карло) в принципе не содержат каких-либо механизмов, позволяющих учесть термическую предысторию стекол, получаемых из расплавов, которая в свою очередь оказывает существенное влияние на многие физические свойства реальных образцов.
Другой подход основан на методах молекулярной динамики. Его суть заключается в явном моделировании самого технологического процесса получения стекол из расплавов. Исходное «кристаллическое сырье» (или даже просто набор атомов заданной стехиометрии, случайно распределенных в расчетной ячейке) нагревается до температур 6000–10000 K. После гомогенизации при высоких температурах система сравнительно медленно охлаждается до комнатной температуры. Процедура проста, позволяет использовать штатные алгоритмы и программное обеспечение методов молекулярной динамики. Тем не менее с этим подходом связаны две серьезные проблемы, затрудняющие создание молекулярных моделей кварцевого стекла, правильно отражающих средний порядок.
Первая причина заключается в том, что типичные времена охлаждения компьютерной модели (десятки-сотни наносекунд, а часто и еще меньше) на много порядков меньше времен охлаждения стекол в обычных технологических процессах (секунды и более, при закалке в воде). Следовательно, при помощи молекулярной динамики, по сути, моделируются стекла с экстремально высокой (для современного уровня развития техники) скоростью закалки на уровне 109 K/с.
Вторая проблема заключается в самих потенциалах, описывающих межатомные взаимодействия. Обычно для таких задач используют эмпирические потенциалы, поскольку расчеты долговременной динамики больших систем «из первых принципов» все еще слишком трудоемки. Эмпирические парные потенциалы с фиксированными зарядами ионов позволяют свести вычислительные затраты к приемлемому уровню. Параметризация этих потенциалов обычно выполняется по экспериментальным (или расчетным) данным, которые связаны с ближним или дальним порядком (спектроскопические данные, параметры решетки кристаллических модификаций и т. п.). Поэтому параметры ближнего порядка получающихся стекол (такие как радиальные функции распределения, функции распределения углов внутри кремнийкислородных тетраэдров, между соседними тетраэдрами и т. п.) достаточно хорошо совпадают с экспериментальными значениями.
Что же касается параметров, которые существенно зависят от перестройки связей в процессе стеклования (например, плотность), то здесь ситуация не так однозначна. В работе [7] выполнен сравнительный анализ параметров моделей стекол, полученных в одинаковых процессах, но с использованием различных потенциалов (в том числе и известного потенциала BKS [8], часто используемого при моделировании силикатных стекол). В результатах этой работы (см. Fig.8 в [7]) можно заметить, что более короткодействующие потенциалы (обозначенные в статье как Takada и Soules) дают более корректные значения плотности стекла, чем потенциалы, имеющие длинные (до 1,1 нм) «хвосты». Последние дают слишком завышенные значения плотности. Причины этого и возможная связь плотности с формой потенциалов в статье не обсуждались. В работе [5], опубликованной раньше, отмечалась важность обрезания длинных «хвостов» потенциала Морзе для более корректного учета процессов разрушения и формирования ковалентных связей в силикатных расплавах. Однако какого-то более детального рассмотрения этого вопроса и его связи с плотностью стекол не проводилось.
Поскольку плотность — один из важнейших параметров, непосредственно характеризующий объем межузельного пространства в кварцевом стекле, то непосредственное использование потенциалов, приводящих к большим ошибкам в плотности стекла, для задач растворения и диффузии газов в стекле неправомерно. Здесь необходимо отметить, что часто используемый на практике способ «коррекции» плотности стекол за счет фиксации объема системы (т. е., по сути, изобарный процесс охлаждения стекла заменяется изохорным) не может быть подходящим решением. Во-первых, в этом случае конечный образец стекла находится, как правило, под отрицательным давлением. Во-вторых, такой способ в принципе не позволяет получать образцы со свободными границами (тонкие мембраны, изолированные наночастицы и т. п.). Поэтому необходимо модифицировать эмпирические потенциалы так, чтобы корректные значения плотности стекол получались именно в изобарном процессе. Один из возможных вариантов вытекает из предыдущих абзацев — попробовать ввести регулируемое дополнительное затухание «хвостов» потенциалов, отвечающих за ковалентную компоненту связей, и более системно оценить их влияние на плотность получающихся стекол. В модифицированных таким способом потенциалах появляются дополнительные степени свободы, позволяющие регулировать плотность стекол, сохраняя при этом параметры ближнего порядка, обеспеченные исходными потенциалами. Изучению и обоснованию такого подхода посвящена данная статья.
Модель
Для простоты ограничимся только чистым кварцевым стеклом. В качестве исходного потенциала выберем потенциал, моделирующий ионно-ковалентный характер связей в явной форме: ионная компонента представлена кулоновcким потенциалом (первое слагаемое в уравнении (1)), а ковалентная — потенциалом Морзе (второе слагаемое):
![]() (1)
(1)
где индексы i и j обозначают индексы атомов кремния и кислорода, r — расстояние между атомами, Z — эффективный заряд ионов, D, α и r0 — параметры потенциала Морзе для каждой пары взаимодействующих атомов.
В работе [6] на основе экспериментальных данных о структурах и физических свойствах большого количества кристаллов оксидов была выполнена параметризация потенциалов вида (1), позволяющая на единой основе моделировать стекла с очень широким набором стеклообразователей и модификаторов. Поэтому удобно выбрать значения соответствующих параметров именно из этой работы. Они приведены в таблице ниже.
|
Связь |
D, эВ |
α , 1/ Å |
r0, Å |
Z |
|
Si-O |
0,340554 |
2.006700 |
2,100000 |
Si +2.4 e |
|
O-O |
0,042395 |
1,379316 |
3,618701 |
O –1.2 e |
|
Si-Si |
0 |
0 |
0 |
|
В принципе, «мягкое» обрезание потенциала Морзе можно выполнить путем умножения второго слагаемого (1) на произвольную монотонную весовую функцию g(r), которая стремится к 1 при малых r и к 0 — при больших. Примерами функций такого вида могут быть дополнительная функция ошибок ![]() , или функция Ферми—Дирака
, или функция Ферми—Дирака ![]() . Для целей данной работы выбор конкретного вида весовой функции не играет существенной роли. В работе [5] использовалась функция Ферми—Дирака. Будем использовать ее и в данной работе. Таким образом, модифицированный потенциал Морзе приобретает следующий вид:
. Для целей данной работы выбор конкретного вида весовой функции не играет существенной роли. В работе [5] использовалась функция Ферми—Дирака. Будем использовать ее и в данной работе. Таким образом, модифицированный потенциал Морзе приобретает следующий вид:
![]() (2)
(2)
где параметр r1 задает радиус обрезания потенциала, а β — крутизну перехода от 1 к 0. На рисунке 2 представлены диаграммы, по которым можно оценить влияние весовой функции на форму потенциальных кривых.
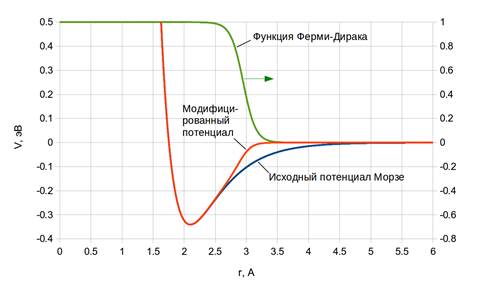
Рис. 2. Модификация потенциала Морзе для связи Si-O. Параметры функции Ферми—Дирака r1 = 2,95 Å, β = 10 Å-1
Модифицированный потенциал (2) содержит два дополнительных параметра. В предварительных численных экспериментах было выяснено, что параметр β не сильно влияет на результирующую плотность стекла. Поэтому для упрощения анализа в данной работе все зависимости строились только от радиуса обрезания r1, а параметр β был зафиксирован на уровне 10 Å-1. Модификации подвергался только потенциал взаимодействия между кремнием и кислородом. Потенциал взаимодействия между атомами кислорода оставался неизменным.
Динамика атомов рассчитывалась при помощи пакета HOOMD-blue [4], весьма эффективно реализующего параллельные вычисления на графических процессорах при помощи технологии CUDA [2]. Использовалась следующая методика приготовления образцов кварцевых стекол.
В кубической ячейке случайным образом (с ограничением минимального расстояния между атомами) размещались атомы кремния и кислорода с учетом стехиометрии. Большая часть расчетов была выполнена с 1000 атомов кремния и 2000 атомов кислорода. Для каждого режима (по параметру r1 и времени охлаждения) инициировалась серия из 6 вариантов начального состояния системы при помощи различной инициализации генератора случайных чисел, задающего начальные координаты и скорости атомов. По этим сериям усреднялись рассчитанные параметры системы (в частности, плотность стекла).
Начальная температура атомов — 6000 K. При расчете использовались периодические граничные условия. Шаг по времени фиксированный — 2 фсек. Интегратор — NPT (подробности — в документации HOOMD-blue [4]). Давление в течение всего процесса поддерживалось фиксированным — 1 атм за счет пропорционального изменения объема ячейки. Для расчета электростатической компоненты использовался метод pppm (Particle-Particle Particle-Mesh), реализованный в HOOMD-blue. После инициализации система выдерживалась в течение 20 пс (10 000 временных шагов) для установления равновесия, после чего производилось медленное линейное снижение температуры системы (в рамках NPT-ансамбля) до комнатной. Время охлаждения варьировалось от 0,1 нс до 100 нс. Скорость расчета (3000 атомов, NPT-ансамбль) при использовании видеокарт ASUS GeForce GTX 780Ti DirectCU II составляла приблизительно 3–4 нс/ч.
Результаты
На рисунке 3 представлена зависимость плотности кварцевого стекла в моделях, полученных в численных экспериментах по методике, описанной выше, от радиуса обрезания r1. Время закалки всех образцов составляло 1 нс. Из графика видно, что плотность стекла в модели, полученной при помощи исходного (немодифицированного) потенциала, составляет приблизительно 2,55 г/см3 (см. правую часть графика, r1 ~ 4,5 Å). Это более чем на 15% превышает экспериментальное значение 2,2 г/см3 (пунктирная линия) [3]. При уменьшении r1 плотность монотонно снижается и при r1 < 3 Å выходит на уровень, близкий к экспериментальному значению (пунктир). Таким образом, параметр r1 действительно является эффективным и однозначным регулятором плотности кварцевого стекла в моделях, получаемых при помощи методов молекулярной динамики.
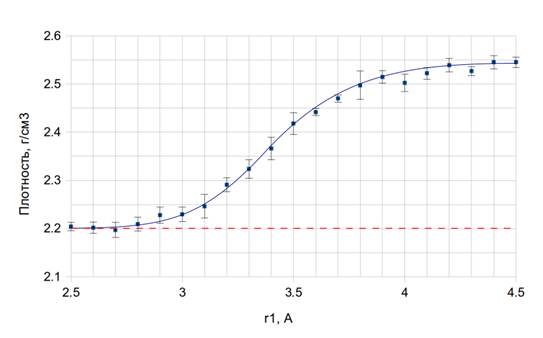
Рис. 3. Зависимость конечной плотности кварцевого стекла от радиуса обрезания потенциала
Отметим, что выход плотности модели на экспериментальное значение происходит при достаточно больших значениях параметра r1 ~ 3 Å. Они существенно превышают длину связи Si-O в кварцевом стекле (~1,62 Å). Поэтому модификация потенциала сказывается только на динамике образования связей Si-O в процессе стеклования, не нарушая при этом параметры ближнего порядка, задаваемые исходным потенциалом. В частности, парные радиальные функции распределения стекол, полученных с исходным потенциалом и с модифицированным, практически совпадают (для ближайших координационных сфер).
Плотность реального кварцевого стекла довольно слабо зависит от скорости закалки. Например, при закалке в воде плотность падает от 2,2115 г/см3 (при времени охлаждения 1,5 с) до 2,2092 г/см3 (при 6 с) [1]. Поскольку в численных экспериментах, как правило, реализуются очень высокие скорости закалки, интересно проследить зависимость плотности стекол в моделях от времени охлаждения. Соответствующая диаграмма представлена на рисунке 4. Из графика видно, что плотность в моделях (как и в реальных стеклах) снижается с увеличением времени охлаждения системы. При изменении скорости закалки на 3 порядка плотность изменяется менее чем на 4 % (точнее, 3,8%). Поэтому какой-либо существенной коррекции регулятора (параметра r1) при изменении скорости закалки не требуется.
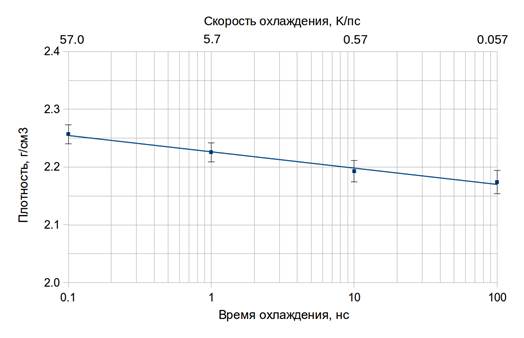
Рис. 4. Зависимость плотности от времени охлаждения.
Параметр r1 = 1,95 Å
Выводы
1. Популярные эмпирические потенциалы, используемые при моделировании кварцевого стекла, часто дают завышенные значения плотности моделей стекол по сравнению с экспериментальными значениями, что делает их малопригодными при создании моделей стекол, предназначенных для моделирования процессов растворения и диффузии газов в них. В статье предложен вариант модификации потенциалов, позволяющий получать корректные значения плотности стекла, сохраняя при этом все параметры ближнего порядка, определяемые исходными потенциалами. Модифицированные эмпирические потенциалы содержат дополнительный параметр (радиус обрезания r1), который может быть определен путем сравнения расчетной плотности стекла с экспериментальной.
2. Показано, что плотность кварцевого стекла в полученных моделях монотонно зависит от параметра r1 в диапазоне его значений от 2,5 Å и выше. При r1 <~ 3 Å плотность близка к экспериментальному значению. Таким образом, параметризация модифицированного эмпирического потенциала однозначна.
3. Оптимальное значение r1 слабо зависит от скорости закалки и составляет приблизительно 2,9–2,95 Å при времени охлаждения системы порядка 10 нс.
Рецензенты:
Парфенов О.Г., д.т.н., заведующий лабораторией плазмохимии и проблем материаловедения Института химии и химической технологии СО РАН, г. Красноярск;
Белобров П.И., д.ф.-м.н., с.н.с., профессор кафедры биофизики СФУ, в.н.с. Института биофизики СО РАН, г. Красноярск.
Библиографическая ссылка
Кухтецкий С.В. КОНТРОЛЬ ПЛОТНОСТИ КВАРЦЕВОГО СТЕКЛА В МОДЕЛЯХ, ПОЛУЧАЕМЫХ МЕТОДОМ МОЛЕКУЛЯРНОЙ ДИНАМИКИ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=19349 (дата обращения: 01.02.2026).



