Одним из основных узлов электрических сетей является трансформатор. При исследовании трансформатора его обмотки принято представлять в виде электрической схемы замещения с сосредоточенными параметрами. Более точная схема замещения должна быть схемой с распределенными параметрами [1, 2]. Особенно это проявляется при диагностике трансформатора с короткими импульсами, пространственная длительность которых много меньше длины обмотки трансформатора [3, 6]. При представлении обмоток трансформатора в виде схемы с распределенными параметрами приходится решать дифференциальные уравнения в частных производных, что гораздо сложнее, чем решать обыкновенные дифференциальные уравнения, возникающие в схемах с сосредоточенными параметрами. Эта сложность проявляется при внесении дополнительной пространственной координаты, которая преобразует схему с сосредоточенными параметрами в схему с распределенными параметрами. Но при этом появляется возможность пространственной локализации повреждений трансформаторных обмоток, что очень важно при его диагностике [1, 3, 6]. Кроме того, в распределенных схемах переходные процессы, происходящие в обмотках трансформатора, можно представить в виде распространения волн, получая при этом более богатую физическую картину явления [3, 5], а следовательно, и более детальное исследование трансформаторных обмоток при аварийных режимах.
Цель работы заключается:
-
в представлении обмотки трансформатора в виде распределенной электрической цепи и исследовании переходных процессов такой цепи в двух случаях: при заземленном конце обмотки и при разомкнутом конце обмотки;
-
в определении начального и установившегося распределения напряжения вдоль обмотки трансформатора при заземленном конце обмотки и при разомкнутом конце обмотки;
-
в поиске возможных путей преодоления перенапряжений, возникающих вдоль обмотки трансформатора.
Постановка задачи и основные соотношения
Электрическую схему с распределенными параметрами можно представить в виде приведенной на рисунке 1, где ![]() – индуктивность и сопротивления на единицу длины обмотки,
– индуктивность и сопротивления на единицу длины обмотки, ![]() – емкость на единицу длины обмотки,
– емкость на единицу длины обмотки, ![]() – емкость обмотки на единицу длины относительно земли.
– емкость обмотки на единицу длины относительно земли.

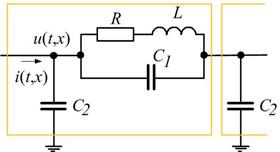
Рис. 1. Обмотка трансформатора и схема замещения элемента обмотки
В соответствии со схемой замещения элемента обмотки трансформатора (см. рис. 1) уравнение трансформаторной обмотки как распределенной системы можно записать в виде:
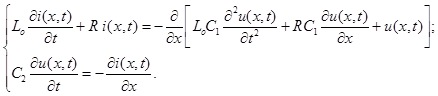 (1)
(1)
Для решения этих уравнений будем использовать операторный метод расчета [4, 5]. Перейдем от оригиналов тока и напряжения к их операторным изображениям, предполагая нулевые начальные условия, получим систему алгебраических уравнений:
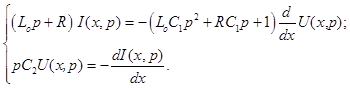 (2)
(2)
Система уравнений (2) может быть переписана в виде:
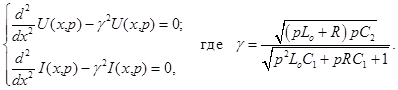 (3)
(3)
Решения уравнений будем искать в виде [1]:
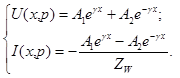 (4)
(4)
Где ![]() волновое сопротивление обмотки, определяемое соотношением:
волновое сопротивление обмотки, определяемое соотношением:
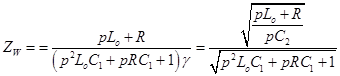
Найдем константы интегрирования ![]() из краевых условий, предполагая, что в конце обмотка заземлена (см. рисунок 2, а), а к началу обмотки подается напряжение
из краевых условий, предполагая, что в конце обмотка заземлена (см. рисунок 2, а), а к началу обмотки подается напряжение ![]() , тогда система уравнений (4) может быть переписана:
, тогда система уравнений (4) может быть переписана:
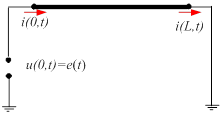 а
а
 б
б
Рис. 2. Краевые условия для обмотки трансформатора, а – заземленной на конце, б – разомкнутой на конце
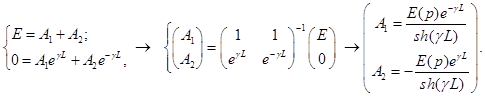
Здесь L – длина трансформаторной обмотки.
Подставляя значения коэффициентов ![]() и
и ![]() , получаем выражения для напряжения и тока вдоль обмотки при ее заземленном конце:
, получаем выражения для напряжения и тока вдоль обмотки при ее заземленном конце:
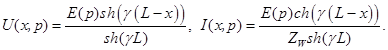 (5)
(5)
Аналогично находим коэффициенты для случая, когда обмотка разомкнута на конце (см. рис. 2, б)
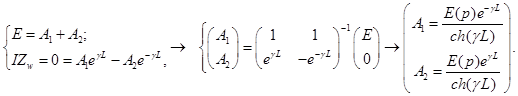
Подставляя значения коэффициентов, получаем выражения для напряжения и тока вдоль обмотки при ее разомкнутом конце:
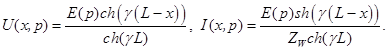 (6)
(6)
Если на вход устройства подать напряжение равное дельта функции Дирака:
![]()
то в пространстве изображений в место ![]() нужно подставить единицу [5].
нужно подставить единицу [5].
Таким образом, получаем передаточные функции для напряжений при заземленном и свободном концах обмотки трансформатора соответственно.
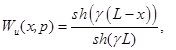
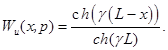
С помощью полученных передаточных функций легко получить установившийся и начальный режимы работы обмотки трансформатора [5]. Учитывая, что при ![]() , по уравнению (3) в установившемся режиме работы обмотки трансформатора при ее заземленном конце мы получаем:
, по уравнению (3) в установившемся режиме работы обмотки трансформатора при ее заземленном конце мы получаем:
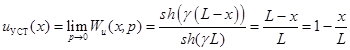 , (7)
, (7)
при ее разомкнутом конце:
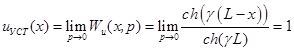 . (8)
. (8)
В другом предельном случае при  по уравнению (3) можно получить начальное распределение напряжения [5]
по уравнению (3) можно получить начальное распределение напряжения [5] ![]() в обмотке трансформатора при ее заземленном конце:
в обмотке трансформатора при ее заземленном конце:
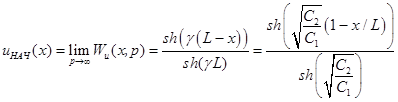 , (9)
, (9)
при ее разомкнутом конце:
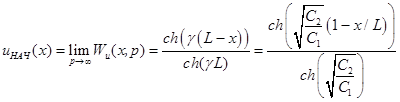 . (10)
. (10)
Теперь найдем распределения напряжения вдоль обмотки трансформатора при воздействии постоянного напряжения в ее начале и при условии заземленного конца обмотки трансформатора. Для этого нужно найти оригинал произведения передаточной функции, умноженной на изображение постоянного напряжения ![]() :
:
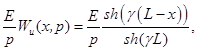
Корни характеристического уравнения определяются следующим образом:
![]()
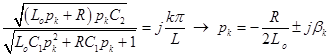 ,
,
где ![]() — собственная частота, определяемая соотношением
— собственная частота, определяемая соотношением 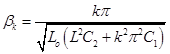 .
.
Тогда выражение для распределения напряжения вдоль обмотки можно записать в виде:
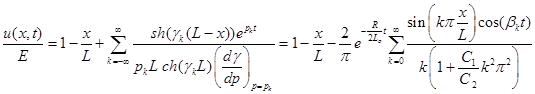 (11)
(11)
Результат расчета распределения напряжения по формуле (11) при параметрах обмотки![]() приведен на рисунке 3.
приведен на рисунке 3.
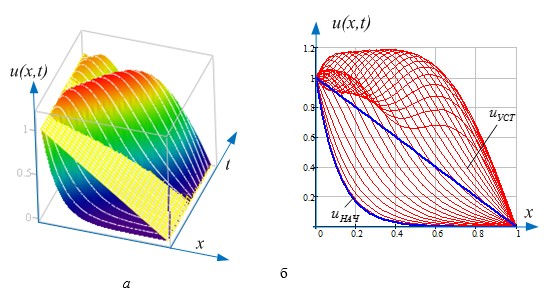
Рис 3. а – Пространственно-временная картина распределения напряжения вдоль обмотки трансформатора. Для сравнения указана плоскость установившегося режима;
б – Та же картина в профиль. Жирные линии показывают начальное значение напряжения ![]() и напряжение при установившемся режиме
и напряжение при установившемся режиме ![]() (обмотка заземлена на конце)
(обмотка заземлена на конце)
Проделав аналогичные операции можно получить распределения напряжения вдоль обмотки трансформатора в случае разомкнутой на конце обмотки:
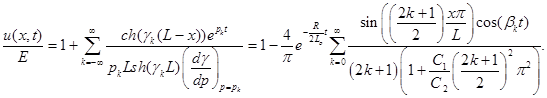 (12)
(12)
Здесь коэффициенты ![]() определяются выражением
определяются выражением 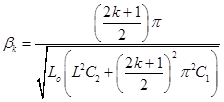 .
.
Результат расчета распределения напряжения по формуле (12) при параметрах обмотки ![]() приведен на рисунке 4.
приведен на рисунке 4.
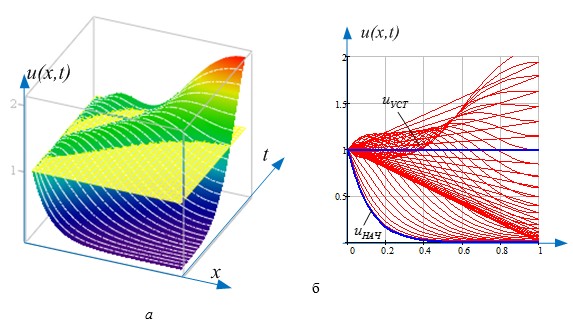
Рис. 4. а – Пространственно-временная картина распределения напряжения вдоль обмотки трансформатора. Для сравнения указана плоскость установившегося режима.
б – Та же картина в профиль. Жирные линии показывают начальное значение напряжения ![]() и напряжение при установившемся режиме
и напряжение при установившемся режиме ![]() (обмотка разомкнута на конце)
(обмотка разомкнута на конце)
Перенапряжения, возникающие вдоль обмотки трансформатора, определяются начальным и конечным распределением напряжения, а также величинами элементов распределенной схемы. Поставим задачу минимизации перенапряжения вдоль обмотки. Для этого запишем дифференциальное уравнение для передаточной функции напряжения, переписав систему (2) в предположении, что величинами элементов можно варьировать:
![]()
Умножая уравнение на p и устремляя p к бесконечности, получаем в случае заземленной обмотки:
![]() ,
,
и уравнение для емкости и его решение:
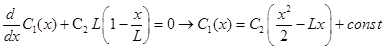
Постоянную надо выбирать так, чтобы при всех возможных x емкость C1 была положительна и превышала естественную емкость обмотки C1.
Выводы
Авторами получена передаточная функция распределения напряжения вдоль обмотки трансформатора, позволяющая определять:
-
начальное и установившееся распределение напряжений;
-
перенапряжения при переходных режимах;
-
оптимальные значения распределенных емкостей.
Эта функция позволяет минимизировать перенапряжения вдоль обмотки.
Чтобы снизить перепады напряжения, можно использовать дополнительные емкости, включая их между обмотками катушки, или создавать кольцевые экраны, охватывающие часть обмотки катушек.
Рецензенты:
Усов Ю.П., д.т.н., профессор кафедры ЭСиЭ ЭНИН ФГАОУ ВО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск;
Курец В. И., д.т.н., профессор кафедры ЭСиЭ ЭНИН ФГАОУ ВО «НИ ТПУ», Национальный исследовательский Томский политехнический университет, г. Томск.
Библиографическая ссылка
Старцева Е.В., Щекотуев А.В., Щекотуев А.В., Исаев Ю.Н. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ТРАНСФОРМАТОРНОЙ ОБМОТКЕ С УЧЕТОМ РАСПРЕДЕЛЕННОСТИ ПАРАМЕТРОВ ОБМОТКИ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=19253 (дата обращения: 12.03.2026).



