Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Еще две программы из разработанного набора приложений предназначены для моделирования электростатического и магнитного полей, генерируемых протекающими в проводах токами [2]. В результате работы приложений на экран выводится картина поля, сформированная линиями равного потенциала и силовыми линиями. Также программы позволяют вычислить напряженность поля и его потенциал в любой точке пространства, окружающего линию.

В настоящее время проблемам техники безопасности уделяется все большее внимание. Для защиты жилых построек предусматриваются молниеотводы, представляющие собой молниеприемник (металлический стержень), токоотводящий шнур и заземлитель [3]. Заземлитель может быть простым металлическим стержнем (чаще всего стальным) или сложным комплексом элементов специальной формы. Для заземления электрооборудования в жилых зданиях и сооружениях используют «горизонтальные» и «вертикальные» заземлители, в обоих случаях электроды располагают в грунте на нужной глубине, чтобы они не были повреждены при работе машин. Глубинные вертикальные электроды наиболее экономичны, достигают хорошо проводящих слоев грунта [4]. Нами предложена простая и удобная в использовании программа численного моделирования стержневого заземлителя для бытовых и промышленных нужд. Программа написана на языке Visual C++ и построена как однодокументное приложение на основе приведенных в статье математических моделей.

Моделирование установившегося и переходного режимов линии электропередач

При расчете переходных процессов в длинных линиях, вызванных прохождением импульсов напряжения и тока, в модели используется частотный (спектральный) метод [5]. При этом спектральную функцию можно определить при помощи прямого преобразования Фурье

(1)

а функцию времени при помощи обратного преобразования Фурье

(2)

Для применения метода необходимо задать нулевые начальные условия и использовать абсолютно интегрируемую функцию f(t). В этом случае спектральную функцию F() искомого напряжения или тока можно найти символическим методом, а затем по (2) определить соответствующую функцию времени.

В данной работе в переходном режиме рассматривается прохождение вдоль линии синусоидального импульса от источника напряжения с длительностью :

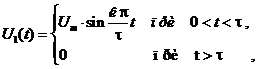                            (3)

который подключается к однофазной линии в момент времени t = 0 (здесь к  целое число, выбираемое из интервала от 1 до 10). Для импульса заданного уравнением (3) по соотношению (1) находим спектральную функцию

, (4)

В результате на основании обратного преобразования Фурье (2) можно определить напряжение и ток в линии как функции координат и времени:

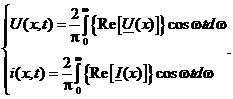(5)

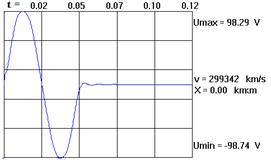
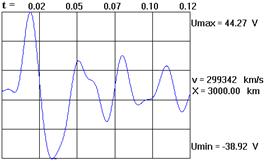
Рис. 1. Распространение импульса в линии

Моделирование электростатического и магнитного полей линии

Еще одной важной задачей, возникающей при проектировании линий электропередач,  является вычисление напряженности электрического и магнитного полей, возникающих при протекании токов в линии.  Математическая модель была разработана на основе уравнений Максвелла, а также с использованием методов зеркальных изображений и наложения [1, 2]. Все программные модули были оформлены как лабораторные работы, предназначенные для использования в учебном процессе или выполнения студенческих исследовательских работ. Полный пакет включал три программы. С использованием одной из них возможно определить распределение скалярного потенциала магнитного поля линии и по полученному распределению построить силовые линии, рассчитать индуктивности проводов и силы, действующие на них.

Следующая программа, входящая в пакет моделирует электростатическое поле линии электропередач. С ее использованием строятся линии равного потенциала, по которым, для получения полной картины поля,  достраиваются линии напряженности.

Еще одна модель предназначена для проведения  исследования зависимости между зарядами (токами) и потенциалами системы проводящих тел, расчета  потенциальных и емкостных коэффициенты, частичных емкостей определения зависимости  частичных емкостей от геометрии системы. Геометрия решаемой задачи иллюстрируется на рис. 2.

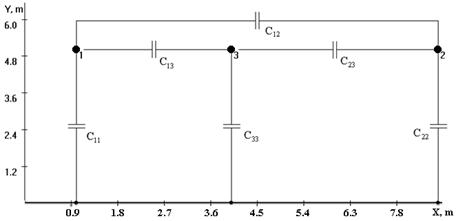
Рис. 2. Геометрия линии электропередач при наличии взаимных емкостей проводов

Исследования, проведенные с использованием данной модели, позволили сделать следующие выводы:

1.    Собственные частичные емкости проводов зависят от расстояния между проводом и “землей”. С увеличением расстояния до “земли” емкости уменьшаются по экспоненциальному закону.

2.    Взаимные частичные емкости проводов зависят не только от расстояния между проводами, но и от геометрии линии. В частности, на значительном удалении от поверхности “земли” минимум взаимной емкости между проводами 1 и 2 достигается, когда третий провод расположен на линии, соединяющей провода 1 и 2. Если система трех проводов расположена на малом расстоянии от “земли”, симметрия задачи нарушается и минимум смещается в направлении от поверхности “земли”.

Таким образом, методы компьютерного моделирования позволяют достаточно полно описать многопроводную линию, получить значительный объем информации об электромагнитном поле, наведенном токами, протекающими в проводах. Кроме этого приложения удобны для использования, с их помощью возможно наглядное представление электростатического и магнитного полей.

Построение модели стержневого заземлителя

Для расчета электрического поля сферического заземлителя диаметром d и с током I0, расположенного на глубине h, возможно использовать метод зеркальных изображений и наложения [3]. На месте зеркального изображения помещается электрод с тем же током I0 (схематически изображение заземлителя показано на рис. 3), где  и , причем 0 < r < ∞ и –∞ < Z ≤ 0. Плотность тока в земле от уединенного шара без учета влияния поверхности земли будет равна при r1 > d/2.

. (6)

тогда согласно закону Ома напряженность электрического поля составит

, (7)

и потенциал

. (8)

где  – удельная проводимость среды, зависящая от физических свойств проводящего материала и температуры. При условии, что φ1 = 0 при r1 → ∞, C1 = 0.

Плотность тока, напряженность и потенциал от изображения заземлителя находятся как

;      ;                                 (9)

Результирующее поле с учетом влияния поверхности земли будет характеризоваться геометрической суммой векторов напряженности E1 и E2, а также суммой потенциалов от каждого из шаров в отдельности

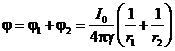.                                       (10)

Все приведенные выше формулы описывали сферический заземлитель [4], тогда как интерес представляет вычисление поля стержня. Для выполнения подобных расчетов стержневой заземлитель можно представить в виде совокупности сферических заземлителей (рис. 4), с каждого из которых стекает ток

, (11)

тогда в некоторой точке N можем записать следующее выражение:

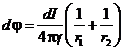, (12)

из которого потенциал определяется как:

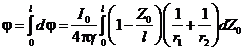, (13)

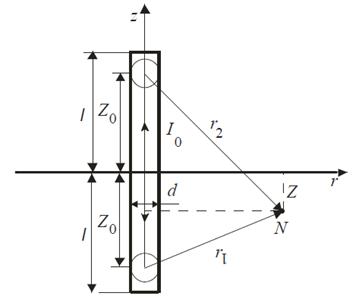
Рис. 3. Стержневой заземлитель как набор сферических заземлителей, где 0 < Z0 < l

На основе приведенного выше математического аппарата была построена программа расчета электростатического поля стержневого заземлителя, которая позволяет определить при заданных значениях проводимости грунта γ, токе заземлителя I0, его длине l и диаметре d сопротивление заземлителя RЗ и распределение потенциала в грунте, также возможным является расчет потенциал на поверхности земли и шагового напряжения. В качестве примера было вычислено распределение напряжения на поверхности для стержня длиной 3 м и диаметром 0,2 м при токе I0 = 20 А (рис. 4). Полученные результаты показали, что значение потенциала уменьшается с увеличением расстояния до стержня и также зависит от диаметра и сопротивления заземлителя.

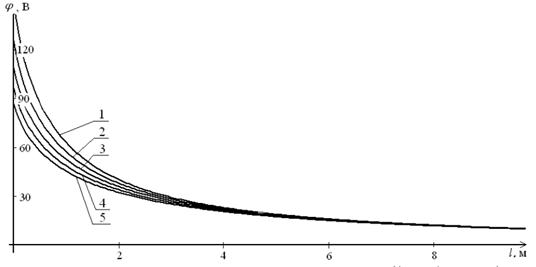
Рис. 4. Изменение напряжения на поверхности земли при увеличении диаметра стержня (l = 3 м, I0 = 20 A). Диаметр стержня/сопротивление, м/Ом: 1) 0,2/16,4; 2) 0,4/13,5; 3) 0,6/11,5; 4) 0,8/10,0; 5) 1,0/9,0

Заключение

В статье описана модель линии электропередач, работающей в переходном и установившемся режимах, модель электростатического и магнитного полей, генерируемых токами в линии, а также модель стержневого заземлителя. С использованием моделей показано, что

1.             Собственные частичные емкости проводов зависят от расстояния между проводом и “землей”. С увеличением расстояния до “земли” емкости уменьшаются по экспоненциальному закону.

2.             Взаимные частичные емкости проводов зависят не только от расстояния между проводами, но и от геометрии линии.

3.             С увеличением длины стержня заземлителя или его диаметра наблюдается уменьшение напряжение на поверхности земли и шагового напряжения. Шаговое напряжение возрастает при увеличении тока стекающего в заземлителя.

Курец В.И., д.т.н., профессор кафедры ЭСиЭ ЭНИН НИ ТПУ, Национальный исследовательский университет, г. Томск;

Исаев Ю.Н., д.ф.-м.н., профессор кафедры ЭСиЭ ЭНИН НИ ТПУ, Национальный исследовательский университет, г. Томск.