В условиях перехода к инновационной модели экономического развития активно обсуждаются наиболее острые и актуальные проблемы модернизации отечественной системы инженерного образования, повышения его качества и оценки эффективности его реформирования [1; 4; 5], создания элитного сектора высшей школы после малоконтролируемого процесса университизации 1990-х гг. [2; 6; 7; 10], в частности в Национальном исследовательском Томском политехническом университете (ТПУ) [3; 9], являющемся одним из ведущих конкурентоспособных российских вузов – получателей субсидий для повышения конкурентоспособности на мировой арене и реализующем систему элитного технического образования (ЭТО) с 2004 года. В настоящее время программа подготовки элитных специалистов в области техники и технологий в ТПУ развивается и совершенствуется для повышения международной конкурентоспособности университета и его выпускников, в том числе с использованием опыта и лучших практик подготовки элитных специалистов в ведущих отечественных и зарубежных вузах, а также с учетом особенностей инженерной деятельности в постиндустриальном обществе, основанном на знании. В связи с этим представляет интерес статистический анализ оценивания значимости качества обучения в системе ЭТО на фоне системы стандартного базового обучения.
Исходная база данных представляет собой категориальные (количество в группе «Отл», «Хор», «Уд», «Неуд» и «Недоп») результаты суммарного осеннего семестрового экзаменационного (ЭКЗ) контроля знаний по дисциплинам математика (МАТ), химия (ХИМ), начертательная геометрия (НАЧ), в котором участвовали студенты-очники первого курса ТПУ набора 2013 г. шести институтов: кибернетики (ИК), природных ресурсов (ИПР), энергетического (ЭНИН), физики высоких технологий (ИФВТ), физико-технического (ФТИ) и неразрушающего контроля (ИНК). При этом выборка ЭКЗ каждой учебной группы разбита на подгруппу ЭКЗЭТО результатов контроля знаний студентов, отделенных в подгруппу ЭТО, и подгруппу остальных ЭКЗБЭ. Заметим, что в случае ХИМ и НАЧ элитники учатся вместе с остальными, что позволяет провести корректное сравнение результатов ЭКЗЭТО и ЭКЗБЭ, а в случае МАТ элитники учатся отдельно от остальных по усложненной программе. Таким образом, рассмотрение проводится в рамках 3-факторной модели результативного признака ЭКЗ: ЭЛИТ*ДИСЦ*ИНСТ (фактор ЭЛИТ с 3-мя уровнями ЭКЗ, ЭКЗБЭ и ЭКЗЭТО; фактор ДИСЦ с 3-мя уровнями МАТ, ХИМ и НАЧ; фактор ИНСТ с 6-ю уровнями ИК, ИПР, ЭНИН, ИФВТ, ФТИ и ИНК). Для каждой группы (подгруппы) было рассчитано значение выборочного среднего (m) по категориальной исходной базе данных (табл. 1).
Таблица 1
Фрагмент категориальной исходной базы данных выборок ЭКЗ, ЭКЗБЭ и ЭКЗЭТО
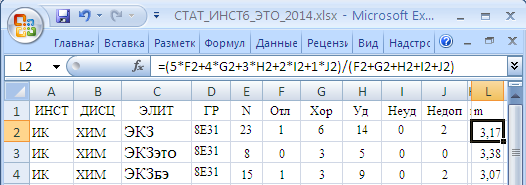
Созданная таким образом в MS Excel база данных выборочного среднего (m) использовалась далее в пакете Statistica 6.1 [8] для статистического анализа результатов ЭКЗ, ЭКЗБЭ и ЭКЗЭТО.
Числовые характеристики выборок ЭКЗ, ЭКЗБЭ и ЭКЗЭТО (среднее m, стандартная ошибка m , границы ±95% доверительного интервала m и объем выборки N - число учебных дисциплино-групп) приведены в табл. 2.
Таблица 2
Числовые характеристики выборок ЭКЗ, ЭКЗБЭ и ЭКЗЭТО
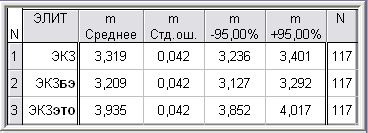
Средний балл ЭКЗЭТО составил 3,935 по 5-балльной шкале, что почти на 
балла выше среднего балла 3,209 выборки ЭКЗБЭ. Графики числовых характеристик выборок ЭКЗ, ЭКЗБЭ и ЭКЗЭТО приведены на рис. 1 (параметрических) и рис. 2 (непараметрических).
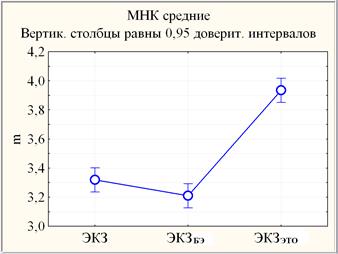
Рис. 1. Линейный график среднего балла с 95%-ным доверительным интервалом результатов ЭКЗ, ЭКЗБЭ и ЭКЗЭТО .
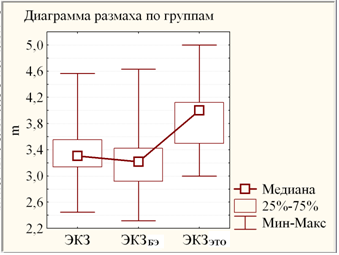
Рис. 2. Диаграммы размаха результатов ЭКЗ, ЭКЗБЭ и ЭКЗЭТО: медианы (квадраты) с квартилями (прямоугольники) и размахами (усы).
Для наглядной оценки значимости отличия результатов ЭКЗ, ЭКЗБЭ и ЭКЗЭТО приведено также совместное распределение (гистограммы) их выборок (рис. 3) по 5-балльной равномерной шкале и показывающее наглядно существенные различия в распределениях ЭКЗБЭ и ЭКЗЭТО.
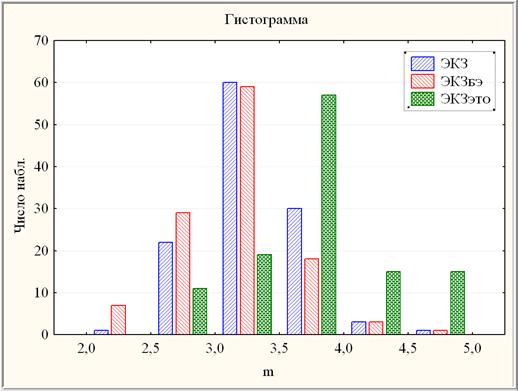
Рис. 3. Составная гистограмма результатов ЭКЗ, ЭКЗБЭ и ЭКЗЭТО ТПУ набора 2013 г.
В случае сравнения средних более чем двух выборок (ЭКЗ, ЭКЗБЭ и ЭКЗЭТО) применяется однофакторный (фактор элитности ЭЛИТ) дисперсионный анализ. В рассматриваемом случае (табл. 3) F-критерий показывает (F ≈ 17,89 / 0,21 ≈ 86,94), что различие между средними баллами m ЭКЗ, ЭКЗБЭ и ЭКЗЭТО высоко значимо (значимо на уровне p < 0,0005).
Таблица 3
Результаты однофакторного дисперсионного анализа влияния фактора ЭЛИТ на переменную ЭКЗ на основе параметрического F-критерия
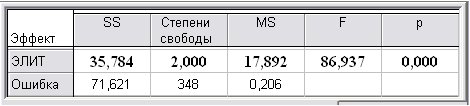
Дисперсионный анализ (параметрический F-критерий (табл. 3) и ранговый критерий Краскела-Уоллиса) оценивает различие по совокупности результатов ЭКЗ, ЭКЗБЭ и ЭКЗЭТО как высоко значимое (на уровне значимости р < 0,0005) за счет высоко значимого отличия результатов ЭКЗЭТО как от ЭКЗ, так и от ЭКЗБЭ согласно различным апостериорным критериям (параметрическим: наименьших значений разности (НЗР), Шеффе, Тьюки и непараметрическому: Краскела-Уоллиса) множественного сравнения, которые обычно применяют после установления неоднородности по совокупности результатов ЭКЗ, ЭКЗБЭ и ЭКЗЭТО. Все критерии множественного сравнения выборок единодушны в оценке высоко значимого (на уровне значимости р < 0,0005) отличия результатов ЭКЗЭТО как от ЭКЗ, так и от ЭКЗБЭ, но разнятся в оценке различия результатов ЭКЗ и ЭКЗБЭ: слабо значимого (0,050 < p=0,066 < 0,100) по НЗР и незначимого (0,10 < p) по остальным критериям. Здесь и в дальнейшем выберем промежуточный вариант – критерий Тьюки ДЗР, согласно которому ЭКЗ и ЭКЗБЭ различаются не значимо, что объяснимо малым числом элитников, а ЭКЗЭТО и ЭКЗБЭ различаются высоко значимо.
В случае сравнения средних выборок ЭКЗ, ЭКЗБЭ и ЭКЗЭТО (влияние фактора элитности ЭЛИТ на переменную ЭКЗ) по дисциплинам (фактор ДИСЦ с тремя уровнями: ХИМ, НАЧ и МАТ) применяется двухфакторный дисперсионный анализ, позволяющий исследовать взаимодействия между факторами и выявлять влияния различных сочетаний факторов друг с другом на результативный признак (переменную ЭКЗ). В общем случае взаимодействие между факторами описывается в виде изменения влияния одного фактора на результативный признак под воздействием другого.
Ниже рассмотрен один из простейших вариантов парного взаимодействия между факторами ЭЛИТ и ДИСЦ (рис. 4), описанный в виде изменения влияния фактора ЭЛИТ на результативный признак ЭКЗ (сравнения средних выборок ЭКЗ, ЭКЗБЭ и ЭКЗЭТО) под воздействием другого фактора ДИСЦ.
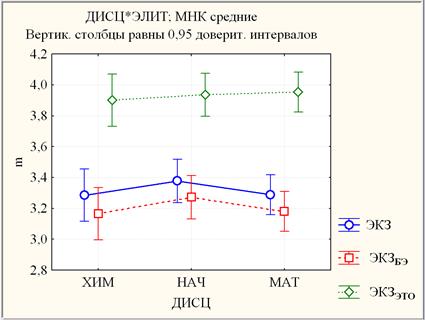
Рис. 4. Линейные графики среднего балла с 95%-ным доверительным интервалом результатов ЭКЗ, ЭКЗБЭ и ЭКЗЭТО по дисциплинам.
Согласно критерию Тьюки ДЗР выборки ЭКЗ, ЭКЗБЭ и ЭКЗЭТО являются однородными по дисциплинам, то есть результаты ЭКЗ, ЭКЗБЭ и ЭКЗЭТО демонстрируют незначимое (на уровне p > 0,99) различие по дисциплинам. При этом результаты ЭКЗБЭ и ЭКЗЭТО различаются высоко значимо (р < 0,0005) по каждой дисциплине: по ХИМ mХИМ*БЭ = 3,166 и mХИМ*ЭТО = 3,901; по НАЧ mНАЧ *БЭ = 3,273 и m НАЧ *ЭТО = 3,936; по МАТ mМАТ*БЭ = 3,180 и mМАТ*ЭТО = 3,954. Учитывая, что в случае ХИМ и НАЧ элитники учатся вместе с остальными, что позволяет сделать корректный вывод о высоко значимом различии mБЭ и mЭТО по этим дисциплинам, а в случае МАТ элитники учатся отдельно от остальных по усложненной программе, то есть mМАТ*ЭТО является заниженным по сравнению с mМАТ*БЭ, то по МАТ различие mБЭ и mЭТО ожидаемо еще более высоко значимым в случае, если бы элитники учились вместе с остальными по одной программе.
Далее рассмотрен еще один простейший вариант парного взаимодействия между факторами ЭЛИТ и ИНСТ (рис. 5), описанный в виде изменения влияния фактора ЭЛИТ на результативный признак ЭКЗ (сравнения средних выборок ЭКЗ, ЭКЗБЭ и ЭКЗЭТО) под воздействием другого фактора ИНСТ, то есть для разных институтов.
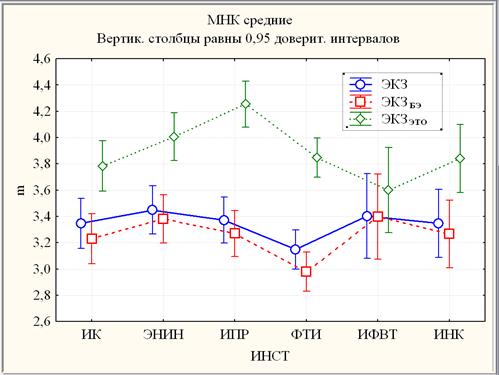
Рис. 5. Линейные графики среднего балла с 95%-ным доверительным интервалом результатов ЭКЗ, ЭКЗБЭ и ЭКЗЭТО по институтам.
На рис. 5 ширина доверительного интервала, определяющая погрешность измерения среднего, обратно пропорциональна 
. Таким образом, более широкие доверительные интервалы m для ИНК (N=11) и, в большей степени, ИФВТ (N=7) объясняются в большей мере сравнительно малыми объемами этих выборок. Однородность независимых выборок ЭКЗ, ЭКЗБЭ и ЭКЗЭТО по институтам была оценена посредством двухфакторного дисперсионного анализа применительно к выборке ЭКЗ. Применение F-критерия, обобщающего t-критерий на число выборок больше двух, привело к выводу о слабой неоднородности сравниваемых институтов. Значимость различий между средними m по институтам оценивалась с помощью апостериорного критерия Тьюки ДЗР, согласно которому выборки ЭКЗ и ЭКЗБЭ являются однородными по институтам, то есть результаты ЭКЗ, ЭКЗБЭ демонстрируют незначимое (на уровне p > 0,93) различие по институтам, а выборка ЭКЗЭТО – слабо значимую неоднородность: mИК*ЭТО = 3,784 и mИПР*ЭТО = 4,256 различаются слабо значимо (0,050 < p=0,061 < 0,100).
Согласно критерию Тьюки результаты ЭКЗБЭ и ЭКЗЭТО различаются высоко значимо (на уровне значимости р < 0,0005) по ЭНИН, ИПР и ФТИ; статистически значимо ((0,005 < p=0,007 < 0, 05) по ИК; незначимо (p > 0,10) по ИНК и в большей степени по ИФВТ.
Результаты проведенного статистического анализа могут быть учтены при принятии управленческих решений в рамках проходящей реформы высшего образования, например дополнительного финансового стимулирования не только по входным результатам ЕГЭ и категории вуза, но и за текущую успешную учебу в вузе.
Выводы
1. Различие результатов ЭКЗБЭ (средний балл mБЭ = 3,209) и ЭКЗЭТО (mЭТО = 3,935) по ТПУ (суммарные по дисциплинам и институтам) оценивается как высоко значимое (на уровне значимости р < 0,0005) согласно различным апостериорным критериям (параметрическим: наименьших значений разности (НЗР), Шеффе, Тьюки и непараметрическому: Краскела-Уоллиса) множественного сравнения.
2. Выборки ЭКЗБЭ и ЭКЗЭТО являются однородными по дисциплинам, то есть результаты ЭКЗБЭ (mХИМ*БЭ = 3,166; mНАЧ *БЭ = 3,273; mМАТ*БЭ = 3,180) и ЭКЗЭТО (mХИМ*ЭТО = 3,901; m НАЧ *ЭТО = 3,936; mМАТ*ЭТО = 3,954) демонстрируют незначимое (на уровне p > 0,99) различие по дисциплинам. Результаты ЭКЗБЭ и ЭКЗЭТО различаются высоко значимо (на уровне значимости р < 0,0005) по каждой дисциплине: по ХИМ mХИМ*БЭ = 3,166 и mХИМ*ЭТО = 3,901; по НАЧ mНАЧ *БЭ = 3,273 и m НАЧ *ЭТО = 3,936; по МАТ mМАТ*БЭ = 3,180 и mМАТ*ЭТО = 3,954.
3. Выборка ЭКЗБЭ является однородной по институтам, то есть демонстрирует незначимое (на уровне p > 0,93) различие по институтам, а выборка ЭКЗЭТО – слабо значимую неоднородность: mИК*ЭТО = 3,784 и mИПР*ЭТО = 4,256 различаются слабо значимо (0,050 < p=0,061 < 0,100). Результаты ЭКЗБЭ и ЭКЗЭТО различаются высоко значимо (на уровне значимости р < 0,0005) по ЭНИН, ИПР и ФТИ; статистически значимо ((0,005 < p=0,007 < 0, 05) по ИК; слабо незначимо (на уровне p = 0,157 > 0,10) по ИНК и в большей степени высоко незначимо (на уровне p = 1,000 > 0,10) по ИФВТ.
Работа выполнена в рамках государственного задания «Наука» № 1.604.2011 и поддержана ФЦП «Научные и научно-педагогические кадры инновационной России» по контрактам П691.
Рецензенты:
Трифонов А.Ю., д.ф.-м.н., профессор кафедры высшей математики и математической физики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Томск;
Арефьев К.П., д.ф.-м.н., профессор кафедры высшей математики, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Томск.
Библиографическая ссылка
Задорожный В.Н. СТАТИСТИЧЕСКОЕ ОЦЕНИВАНИЕ ЗНАЧИМОСТИ КАЧЕСТВА ЭЛИТНОГО ТЕХНИЧЕСКОГО ОБРАЗОВАНИЯ // Современные проблемы науки и образования. – 2015. – № 1-1. ;URL: https://science-education.ru/ru/article/view?id=19217 (дата обращения: 10.10.2024).