Автоматизированная обучающая система (АОС) представляет собой обучающую подсистему, включающую в себя модель обучающего и компьютерную обучающую систему (КОС). Компьютерная обучающая система (КОС) — это элемент АОС, включающий ПК и осуществляющий автоматическую реализацию функций по управлению обучением и отображению обучающей информации посредством программной реализации соответствующих алгоритмов управления [2].
 |
Рис. 1. Структура системы обучения
Таким образом, управление обучением в АОС – это выбор путей достижения максимально возможной эффективности функционирования учебной структуры в конкретных условиях, т.е. при установленном контингенте обучаемых, составе учебных задач и имеющихся в наличии ресурсов обучения, таких как время, средства профессиональной подготовки, преподаватели и т.д. Система управления процессом обучения – сложная система, которую можно представить в виде подсистем, реализующих следующие функции: выбор сценария тренировки; определение состава учебных задач и последовательности их отработки для каждого субъекта обучения; управление ходом занятия, тренировки и оценка ее результатов. В этом случае структуру взаимодействия подсистем, образующих в своей совокупности схему управления процессом обучения с применением технических средств обучения (ТСО), можно представить как показано на рисунке 2.
Циклический процесс обучения, представленный на рисунке 2, предполагает наличие обратной связи, постоянных количественных изменений с использованием статистических моделей, планирования и обеспечения устойчивости в обучении.
Принятие решений для менеджмента процессов обучения [1] требует использования принципов управления, в частности принципов модельного управления. В составе модели управления процессом обучения можно выделить: модели усвоения; модели среды обучения; модели алгоритмов обучения.
Рассмотрим реализацию модели среды обучения. Процесс обучения осуществляется по следующему алгоритму. Обучаемому предъявляется порция обучающей информации (ОИ). Затем, для определения качества усвоения им данной порции ОИ, ему задается один или несколько вопросов. В системе осуществляется проверка правильности ответов и определяется следующая порция ОИ, которая сообщается обучаемому.
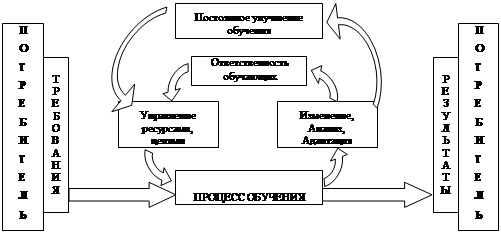 |
Рис. 2. Структурная схема процесса управления процессом обучения
Последовательность предъявления обучаемому той или иной порции ОИ определяется обучающей программой, которая строится согласно алгоритму обучения, опирающемуся в свою очередь на некоторую модель процесса обучения. Широкое распространение получили два типа моделей — модели линейного и разветвленного процесса обучения.
Цель обучения в линейной модели процесса обучения состоит в том, чтобы предъявить обучаемому все порции ОИ. В разветвленной схеме целью обучения является, как и в линейной, усвоить все порции обучающей информации из имеющихся. В моделях с разветвленным внешне регулируемым процессом обучения целью обучения является доведение обучаемого до последней порции обучающей информации.
Рассмотрим модель обучаемого (модель усвоения). Под ней понимается представление того процесса, который происходит в обучаемом в результате восприятия им той или иной обучающей информации. Тогда модель обучаемого есть модель научения.
Исключительно важную роль в изучении процессов научения и обучения играет исследование памяти. Память является одним из важнейших психических процессов, реализующих усвоение знаний. Начало экспериментальной психологии памяти связано с опытами Г. Эббингауза [6]. Он первый разработал количественные методы исследования запоминания и забывания, и им была построена кривая изменения объема памяти в зависимости от времени, прошедшего после запоминания, т. е. кривая времени забывания (рис. 3). Эту кривую называют кривой забывания (или сохранения). Она выражает объем памяти через разные промежутки времени в «процентах сбережения». При этом под объемом памяти (кратковременной) понимается наибольшее число единиц запоминаемого материала, которое может быть сразу воспроизведено при одном повторении [1, 3, 6]. Что касается долговременной памяти, то измеряют число повторений, необходимых для запоминания и безошибочного воспроизведения, предъявленного для запоминания материала, и объем памяти определяют как отношение числа запоминаемых символов к числу повторений [1, 3]. При этом кривая Эббингауза — это объем памяти как функция времени. Описывается она следующим выражением [6]:
![]() ,
,
где b – процент удержанного в памяти материала в момент эксперимента, t – время с момента полного освоения материала в часах, с и k – константы, получаемые методом наименьших квадратов по экспериментальным данным.

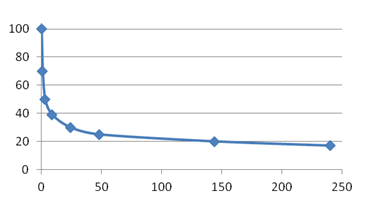
Рис. 3. Кривая Эббингауза
Л. Терстоун предложил следующее аналитическое выражение (гиперболический закон обучения):
![]() ,
,
где y – усвоение, n – число испытаний, a и с – константы; b – скорость научения.
В дальнейшем [6] процесс обучения рассматривался как стохастический процесс, поэтому модель Терстоуна приобретает вид:
![]() ,
,
где y интерпретируется как вероятность приобретения навыка (или правильного ответа) в n-ом испытании.
Линейная модель Буша—Мостеллера определяет вероятность усвоения какой-либо единицы знания после прохождения n-го этапа обучения:
![]() ,
,
где q – вероятность усвоения знаний после первого этапа обучения, с – постоянная, характеризующая скорость обучения. Примером использования линейной модели Буша—Мостеллера является обучение операторов навыкам работы на пультах управления, работы по приему, переработке и выдаче информации в зависимости от числа упражнений [6].
В настоящее время вопросы научения опираются на статистическую теорию обучения [1, 4, 5, 7]. В ней рассматриваются случайные процессы усвоения и забывания (приобретения и утраты умения, навыка).
Пусть существует программа контроля, содержащая N>>1 вопросов и заданий, причем в любой момент времени каждый вопрос может быть усвоен или не усвоен. Эти состояния обозначаются логическими единицей и нулем. Если в момент времени t = 0 учебный материал по какому-либо вопросу изучен и при задании этого вопроса обучаемый дает правильный ответ, а при повторении того же вопроса в момент t=t — неправильный ответ, то t соответствует времени забывания.
Предположим, что время забывания t является неотрицательной непрерывной случайной величиной, имеющей функцию распределения вероятностей
P(t)=P{t<t} (1)
с производной p(t)=P'(t). P(t) есть вероятность неправильного ответа до момента времени t. Тогда величина:
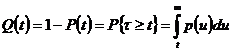 (2)
(2)
соответствует вероятности получения правильного ответа на вопрос в интервале (0, t), т. е. вероятности того, что в интервале (0, t) вопрос по какому-либо элементарному высказыванию не будет забыт.
Зная изменение во времени вероятности правильного ответа Q(t), можно определить математическое ожидание времени забывания вопросов определенного типа тем или иным обучаемым:
![]() (3)
(3)
Аналогично можно определить дисперсию времени забывания:
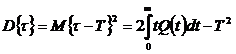 (4)
(4)
Введем характеристику знания обучаемого по какому-либо вопросу — интенсивность забывания или интенсивность потока забывания учебного материала. Пусть в момент времени t=0 все N вопросов программы усвоены обучаемым, а вероятность правильного ответа на каждый из них в момент времени t равна Q(t). Предположим, что знания по забытым вопросам не восстанавливаются (повторение отсутствует). При этом через время t в среднем будет забыто число вопросов M(t) = NP(t). Следовательно, число незабытых вопросов равно: N – М (t) =NQ(t). Зная M(t), можно определить частоту забывания вопросов:
![]() (5)
(5)
где р(t) — плотность вероятности неправильного ответа. Тогда отношение l(t) частоты забывания к ожидаемому числу незабытых вопросов в интервале времени (0, t)
![]() (6)
(6)
Величина l(t) представляет собой плотность условной вероятности неправильного ответа в момент времени t при условии, что до этого момента вопрос не был еще забыт. Назовем ее функцией интенсивности забывания (или просто интенсивностью забывания). Она может возрастать или убывать с течением времени.
Величины Q(t), p(t) и l(t) связаны между собой:
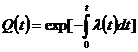 ,
, 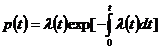 (7)
(7)
Интенсивность забывания l(t) имеет следующий смысл. Величина l(t)Dt представляет собой вероятность того, что обучаемый, знающий учебный материал по какому-либо вопросу в интервале времени (0, t), забудет его в интервале времени (t,t+Dt). Таким образом, среднее время забывания равно 1/l (с).
Законы распределения случайной величины — времени забывания — могут быть различными и определяются в зависимости от характера деятельности обучаемого, типологии его личности, внешних условий. В [7] для описания процесса забывания предлагается использовать экспоненциальное распределение, распределения Вейбулла, Эрланга и гамма-распределение.
В случае экспоненциального распределения
![]() ,
,
![]()
Тогда выражения для математического ожидания, дисперсии времени забывания и интенсивности забывания имеют вид:
![]() ;
; ![]() ;
l(t)= l (9)
;
l(t)= l (9)
При l=const вероятность правильного ответа на вопрос в интервале (t,t+Dt) не зависит от t, а зависит от ширины интервала Dt.
При распределении Эрланга плотность и функция распределения времени забывания определяются следующим образом:
![]() ;
(10)
;
(10)
![]() ,
(11)
,
(11)
где а – положительное целое число. Экспоненциальное распределение есть частный случай распределения Эрланга при а=1.
Распределение Вейбулла. Если l(t)= lt, то
![]() ,
(12)
,
(12)
в общем случае при l(t)= lta
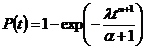 ,
, 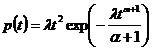 (13)
(13)
Таким образом, экспоненциальное распределение есть частный случай закона Вейбулла при a=0. Тогда путем выбора параметров a и l можно достичь более точного соответствия экспериментальных данных и теоретического распределения.
Допустим, после изучения i-го вопроса в момент времени t=0 обучаемый дает на него правильный ответ. Через время t1 он его забывает. В этот момент происходит в соответствии с теорией «внезапного» обучения [7] восстановление знаний обучаемого. Процесс забывания и восстановления знаний i-го вопроса можно представить в виде чередующихся интервалов забывания или сохранения (состояние Е0) и восстановления знаний (состояние E1) (рис. 4). Рассматриваемый процесс может быть описан следующим образом. В момент времени t=t01i в соответствии с учебной программой начинается изучение материала по какому-либо вопросу. Для этого требуется время Q1. Затем начинается забывание данного вопроса. Длительность этого промежутка времени равна t1. Для повторного восстановления знаний по данному вопросу обучаемому требуется время Q2. Пусть моменты времени
tn1i=Q1 +t1 +Q2 +t2 +…+Qn +tn
tn2i=Q1 +t1 +Q2 +t2 +…+Qn , т=1,2,…
соответственно моменты забывания и восстановления знаний.
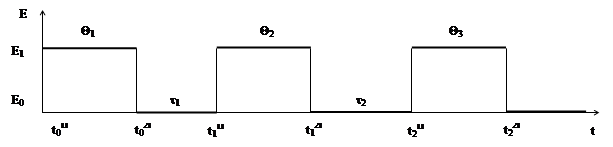 |
Рис. 4. Чередующиеся процессы забывания и восстановления
Математической моделью рассматриваемого процесса является соответствующий случайный процесс. Если все интервалы tj имеют одно и то же распределение F(t), а все интервалы Qj— одно и то же распределение G(t), то математической моделью процесса забывания и восстановления знаний является альтернирующий процесс восстановления.
Таким образом, каждому вопросу или отдельной теме соответствует два отдельных потока: поток учебного материала (П1i) и поток усвоения или восстановления знаний (П2i).
Поток учебного материала П1i образован моментами времени t01i, tl1i, t21i, ...,. Момент времени tlio соответствует моменту первого изложения материала по i-му вопросу в соответствии с учебной программой, последующие же моменты времени tl1i, t21i , … соответствуют моментам забывания знаний по данному вопросу.
Поток усвоения или восстановления знаний П2i для i-го вопроса образуется моментами времени t02i, tl2i, t22i, ...,. При этом t02i соответствует моменту времени усвоения i-го вопроса после его первого изложения, моменты tl2i, t22i, ..., соответствуют моментам восстановления знаний после их забывания.
Тогда суммарный поток учебного материала:
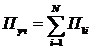 , (14)
, (14)
Аналогично, поток усвоения и восстановления знаний:
![]() (15)
(15)
Среди суммарных потоков Пуч и Пвос в первую очередь рассмотрим простейшие или стационарные пуассоновские потоки. Вероятность появления k событий и математическое ожидание числа событий в интервале времени (0, t) равны:
![]() ,
, ![]() (16)
(16)
Можно показать, что суммарный поток Пуч, получающийся в результате суммирования простейших потоков программы подготовки по отдельным вопросам, является простейшим:
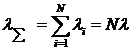 ,
при l1=l2=…=lN=l
,
при l1=l2=…=lN=l
Аналогичные соотношения справедливы для простейшего потока восстановления знаний.
Анализ процесса обучения, рассматриваемого как совокупность моделей обучения и обучаемого и представленного в виде простейших стохастических потоков, дает возможность создать модель обучения без серьезных ограничений, т. е. задача оптимизации успешно решена.
Рецензенты:Рыбакова Н.А., д.п.н., доцент, заведующий кафедрой психологии, педагогики и социально-гуманитарных дисциплин, ЧОУ ВО «Московский университет им. С.Ю. Витте», г. Москва;
Парфенова М.Я., д.т.н., профессор, руководитель научно-исследовательского центра, ЧОУ «ВО Московский университет им. С.Ю. Витте», г. Москва.
Библиографическая ссылка
Афанасьев Ю.И. ОПТИМИЗАЦИЯ МОДЕЛИ УПРАВЛЕНИЯ ПРОЦЕССОМ ОБУЧЕНИЯ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=19196 (дата обращения: 12.03.2026).



