Электрострикционная
сила может достигать больших величин уже при интенсивности падающего излучения
в несколько мВт. Например,
экспериментально наблюдалось однолучевое удержание (левитация) диэлектрических
частиц (стекло) размером до 10 мкм в воде в луче аргонового лазера (![]() мкм,
P=100 мВт),
что свидетельствует об эффективности электрострикционных сил. Концентрационная
оптическая нелинейность исследовалась экспериментально и теоретически в
различных средах – газах, суспензиях, микроэмульсиях [4–6]. При малых
интенсивностях излучения отклик среды соответствует кубичной нелинейности,
поскольку изменение концентрации частиц (и, соответственно, эффективного
показателя преломления среды) пропорционально интенсивности излучения. Данный
тип нелинейности использовался для записи динамических голограмм, исследовалась
самофокусировка излучения [4–5].
мкм,
P=100 мВт),
что свидетельствует об эффективности электрострикционных сил. Концентрационная
оптическая нелинейность исследовалась экспериментально и теоретически в
различных средах – газах, суспензиях, микроэмульсиях [4–6]. При малых
интенсивностях излучения отклик среды соответствует кубичной нелинейности,
поскольку изменение концентрации частиц (и, соответственно, эффективного
показателя преломления среды) пропорционально интенсивности излучения. Данный
тип нелинейности использовался для записи динамических голограмм, исследовалась
самофокусировка излучения [4–5].
Целью данной работы является теоретический анализ самовоздействия светового пучка в прозрачной дисперсной среде при больших интенсивностях излучения, когда, в отличие от работы [5], изменение концентрации не обязательно мало.
Мы будем рассматривать жидкофазную среду с наночастицами (дисперсная фаза), находящуюся под воздействием лазерного излучения с гауссовым профилем интенсивности [5].
Пусть распределение интенсивности падающего излучения в плоскости слоя среды имеет гауссов вид
![]() ,(1)
,(1)
где ![]() интенсивность
световой волны в центре пучка,
интенсивность
световой волны в центре пучка, ![]() радиус
гауссова пучка.
радиус
гауссова пучка.
Балансное уравнение,
описывающее динамику концентрации наночастиц в жидкофазной среде с учётом диффузионного
и электрострикционногопотоков (![]() -
электрострикционный поток), можно записать в виде [5]:
-
электрострикционный поток), можно записать в виде [5]:
![]() .
(2)
.
(2)
Здесь приняты следующие обозначения: ![]() – объемная концентрация дисперсных
частиц,
– объемная концентрация дисперсных
частиц, ![]() – коэффициент диффузии,
– коэффициент диффузии, ![]() ,
,
![]() ,
, ![]() -
подвижность микрочастицы,
-
подвижность микрочастицы, ![]() –
размер частицы,
–
размер частицы, ![]() –
вязкость жидкости,
–
вязкость жидкости, ![]() –поляризуемость
частиц,
–поляризуемость
частиц, ![]() – постоянная Больцмана,
– постоянная Больцмана, ![]() – эффективный показатель преломления
среды,
– эффективный показатель преломления
среды, ![]() – скорость света в вакууме.
– скорость света в вакууме.
В стационарном режиме уравнение (2) упрощаетcя:
![]() .
(3)
.
(3)
Общее решение уравнения (3) ищем в виде
![]() , (4)
, (4)
где![]() ,
, ![]() нормировочная константа. Введем
безразмерный параметр интенсивности излучения
нормировочная константа. Введем
безразмерный параметр интенсивности излучения ![]() .
Для немалых изменений концентрации частиц (при большой интенсивности излучения)
имеем
.
Для немалых изменений концентрации частиц (при большой интенсивности излучения)
имеем ![]() >>1. Константу
>>1. Константу ![]() находим из условия нормировки
(сохранения числа частиц)
находим из условия нормировки
(сохранения числа частиц)
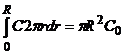 ,
(5)
,
(5)
где ![]() –
радиус цилиндрической кюветы.
–
радиус цилиндрической кюветы.
Принимая ![]() , в результате численного расчета имеем:
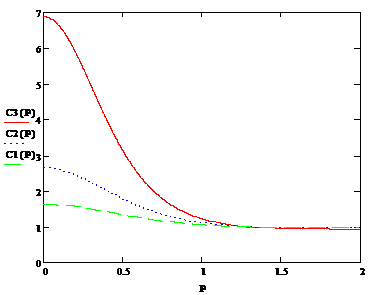
при α1=0.5 (B1=0.989); при α2=1 (B2=0.974); при α3=2 (B3=0.931). Используя (4–5), получаем зависимость
концентрации от приведенного расстояния от оси кюветы
, в результате численного расчета имеем:
при α1=0.5 (B1=0.989); при α2=1 (B2=0.974); при α3=2 (B3=0.931). Используя (4–5), получаем зависимость
концентрации от приведенного расстояния от оси кюветы ![]() (рис.1).
(рис.1).
|
|
|
Рис.1. Зависимость концентрации Сn(ρ) от приведённого радиуса для разных значений интенсивности излучения (α1,α2,α3 – соответственно) |
Данный результат показывает, что концентрация экспоненциально зависит от интенсивности (в отличие от обычной кубичной нелинейности) [1–6].
Для оптической силыконцентрационной линзы имеем из (4–5) выражение [2]:
![]() , (8)
, (8)
где ![]()
Для частиц с радиусом, много меньшим длины волны излучения l, показатель преломления среды пропорционален концентрации частиц [5]:
![]() , (9)
, (9)
где ![]() ;
; ![]() – показатели преломления вещества
дисперсионной среды и дисперсной фазы соответственно,
– показатели преломления вещества
дисперсионной среды и дисперсной фазы соответственно, ![]() – объемная доля дисперсной среды.
– объемная доля дисперсной среды.
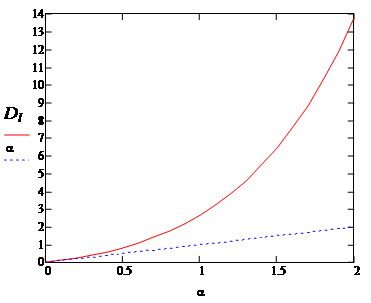
Поскольку фокус линзы растет экспоненциально, то справедливо назвать ее «суперлинзой».
|
|
|
Рис.2. Зависимость оптической силы нелинейной линзы от нормированной интенсивности излучения
|
Максимальная
интенсивность, ![]() для которой
выполняется (3), соответствует
для которой
выполняется (3), соответствует ![]() , где
, где ![]() - объем одной частицы (т.е. объемная доля
частиц
- объем одной частицы (т.е. объемная доля
частиц![]() ),
),
![]() ,
(9)
,
(9)
где ![]() –
начальная объемная доля частиц,
–
начальная объемная доля частиц, ![]() –
интенсивность насыщения, при которой изменение концентрации становится
сравнимым с начальной ее величиной. Поскольку обычно
–
интенсивность насыщения, при которой изменение концентрации становится
сравнимым с начальной ее величиной. Поскольку обычно![]() ,
то максимальная интенсивность может быть намного больше интенсивности
насыщения, что представляет особенный интерес для импульсных режимов
взаимодействия излучения с дисперсными средами [5–8].
,
то максимальная интенсивность может быть намного больше интенсивности
насыщения, что представляет особенный интерес для импульсных режимов
взаимодействия излучения с дисперсными средами [5–8].
Полученные результаты актуальны для нелинейной оптики дисперсных жидкофазных сред [2–6], а также для оптической диагностики таких сред (например, для термооптической спектроскопии [7–10]).
Рецензенты:Карпец Ю.М., д.ф.-м.н., профессор по кафедре физики, профессор кафедры «Физика и теоретическая механика» ФГБОУ ВПО Дальневосточный государственный университет путей сообщения,г. Хабаровск;
Криштоп В.В., д.ф.-м.н., профессор по кафедре физики, проректор по учебной работе ФГБОУ ВПО Дальневосточный государственный университет путей сообщения Министерства транспорта РФ, г.Хабаровск.
Библиографическая ссылка
Иванова Г.Д., Кирюшина С.И., Мяготин А.В. НЕЛИНЕЙНАЯ ЛИНЗА В ДИСПЕРСНОЙ СРЕДЕ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=19194 (дата обращения: 12.03.2026).