Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Широкое применение алгоритмов параллельной обработки информации в современных информационно-управляющих системах привело к открытию новой области исследований, связанной с проблемами эффективного формирования параллельных процессов в системах данного класса. Между реализацией алгоритмов на классической однопроцессорной архитектуре ЭВМ и реализацией тех же алгоритмов на параллельных вычислительных системах существуют принципиальные различия [1, 7]. В [8] показано, что, чем выше быстродействие параллельной вычислительной системы, достигаемое за счет архитектурных решений, тем более ограничен класс управляющих алгоритмов информационно-управляющих систем, которые на ней могут быть эффективно реализованы.

Эффективное формирование параллельных процессов программного обеспечения является сложной, но крайне важной и актуальной на сегодняшний день задачей [9]. На ее решение существенно влияют индивидуальные особенности параллельных систем. Несомненно, такие задачи можно решать для каждой информационно-управляющей системы в отдельности, но уже сейчас существует большое количество различных методов и средств, применяемых в информационно-управляющих системах, и создание конкретного программного обеспечения для каждой системы является неприемлемым. Поэтому эффективное формирование параллельных процессов должно начинаться с построения математической модели работы большого числа узлов с изменяемыми (в общем случае) связями и с анализа на основе данной модели особенностей информационных потоков, проходящих через всю совокупность узлов [6]. Это позволит разработать методы и алгоритмы формирования параллельных процессов в информационно-управляющих системах, а также предложить методы их оптимизации [4].

Одним из способов описания процессов в информационно-управляющей системе является представление структуры выполнения задач системы с помощью сетевой  модели [3]. Математический аппарат сетевого моделирования позволяет описать процессы, протекающие в системе, и произвести оптимизацию с целью получения такого плана выполнения работ системы, который бы позволял рационально использовать ресурсы системы и минимизировать время выполнения всего проекта [2, 5].

Далее будет рассмотрена задача формирования оптимального расписания выполняемых операций в информационно-управляющей системе, объединенных общими ограничениями на ресурсы.

Модель формирования оптимального плана

Положим, что имеется план, который содержит множество логически взаимосвязанных между собой операций (задач) V. В информационно-управляющей системе присутствует L видов ресурсов, все они используются для выполнения данного плана задач.

Операции (задачи) обозначаются как (i, j), где i – начальное, а j – конечное событие задачи. Каждая операция может выполняться только одним определенным типом ресурса. Работы, выполняемые одним видом ресурса, выделяются во множество .

Далее, для каждой операции (i, j) обозначим: t(i, j) – продолжительность ее выполнения, tрн(i, j) – наиболее ранний момент начала операции, tпо(i, j) – наиболее поздний момент окончания операции. Известны директивные сроки начала Dн и окончания Dо проекта. Для корректности задачи необходимо выполнение условия K ≤ Dо – Dн, где K – длина критического пути плана.

Планируемый период [Tн, То] (Tн и То совпадают с директивными сроками) разбивается на f интервалов, каждый продолжительностью τk (). Задается наличное количество используемых ресурсов для каждого вида  на k-м интервале, суммарная трудоемкость выражается как .

Примем следующие обозначения: tн(i, j) и tо(i, j) – моменты времени начала и окончания работ, w(i, j)k – трудоемкость, c(i, j)k  – полезные трудозатраты в стоимостном выражении. Данные характеристики относятся к той части продолжительности работы t(i, j), которая покрывается результатом τk. В связи с тем, что в произвольный момент времени состояние процесса формирования характеризуется значениями tн(i, j) и tо(i, j), "(i, j), эти значения можно рассматривать как фазовые координаты объекта управления.

Получаем задачу нахождения таких значений tн(i, j) и tо(i, j), "(i, j), которые позволяли бы достичь с учетом всех ограничений номинальную и, по возможности, равномерную загрузку всех видов ресурсов на протяжении всего планируемого периода.

Представленную выше задачу формализуем следующим образом.

Необходимо, чтобы движение объекта в фазовом пространстве удовлетворяло ограничениям на сроки выполнения проекта:

,   ,                                                  (1)

и ограничениям на порядок выполнения задач, которые заданы топологией сетевой модели (комплексом информационно и по управлению взаимосвязанных задач информационно-управляющей системы):

G(J, V),                                                                        (2)

где J – множество вершин.

Положим Rk – подмножество задач, которые покрываются k-м интервалом времени длительностью τk, k=, .

Данная задача представляет собой задачу сетевого планирования на подмножестве Rl   с учетом (1) и (2), которую можно представить в виде целочисленной модели:

                                                          (3)

,                                                 (4)

где

            Здесь jk(l) – функция штрафа, далее о ней будет сказано подробнее.

Чтобы достичь оптимального управления на всем планируемом периоде [Tн, То], необходимо также достичь оптимальности управления на каждом интервале τk. Получаем функцию, характеризующую эффективность управления, следующего вида:

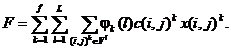                                          (5)

Задача (1)-(5) полностью охватывает специфику процессов информационно-управляющих систем, а также их особенности.

В результате, максимизируя функционал (5), можно получить минимум себестоимости выполнения всех операций.

Для решения описанной выше задачи предлагается использовать метод случайного поиска с пересчетом с переменной величиной шага. Данный метод осуществляет направленный поиск как при достижении допустимой области поиска, определяемой заданными ограничениями, так и непосредственно в допустимой области.

Перейдем к поэтапному описанию процедуры решения задачи.

Многоэтапная процедура оптимизации сетевой модели

Этап I. На основе топологии сети (2) и известных tрн(i, j) и tпо(i, j) производим расчет длины критического пути – k, а также резервов времени всех работ:

P(i)= tпо(i, j) – tрн(i, j) + Dо – Dн – k.

Берем величину шага Ш0 = . Максимум вычисляется по всем задачам плана.

Этап II. Положим начальную точку поиска То (положение начал задач) по следующему правилу:

 tрн(i, j) +, "(i, j).

Этап III. В полученной на предыдущем шаге точке проверяем, выполняется ли условие (4) для каждого k-го интервала . Это необходимо, чтобы проверить, не превышает ли ожидаемая потребная трудоемкость наличную трудоемкость по каждому виду ресурса  :

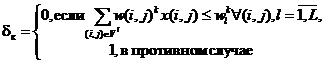
Этап IV. На данном этапе выясним, на каких интервалах условие (4) не выполняется.

Определим

Целочисленная функция D представляет собой функцию качества при достижении допустимой области. Если значение D, полученное в новой точке, меньше, чем в предыдущей, значит, шаг является подходящим.

При D > 0 переходим к этапу VIII, поскольку допустимая область уже достигнута; если же D = 0, то переходим к вычислению функции качества (5), так как найденная точка находится внутри допустимой области.

Этап V. В  функционале (5) jk(l) – функция штрафа за невыполнение условия:

 ,                                 (6)

Это условие устанавливает некоторые допуски D1 и D2 для наличного ресурса l-го вида в произвольный момент.

Функция jk(l) определяется по формуле:

,

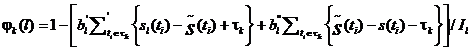где ti – моменты времени, в которые происходит изменение потребного количества ресурса (ti = tн(i, j) или ti = tн(i, j) + t(i, j)); – суммарное количество l-го вида ресурса, требуемого в момент времени ti;  сумма по тем ti, в которых происходит нарушение условия (6) справа (перегрузка);  и – коэффициенты штрафа за недогрузку и перегрузку,  соответственно, Il – число моментов ti на k-м интервале – τk.

Запоминаем значение F0 = F(T0) и переходим этапу VI. Если h ≥ 1 (h – номер шага поиска), то переходим к этапу Х.

Этап VI. На данном этапе моделируется М-мерный единичный случайный вектор . Данный вектор является равномерно распределенным по всем направлениям фазового пространства. Обозначим координату этого вектора как x(i, j), она соответствует работе (i, j).

Этап VII. Определим переход из точки Tη в точку Tη + 1 по формулам:

 

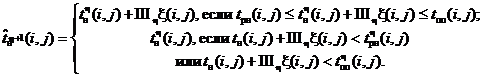
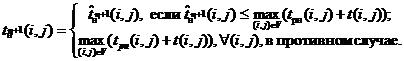
Для осуществления возврата в точку Тη необходимо вычислить величины

которые хранятся в памяти до следующего шага. Переходим к этапу III.

Этап VIII. Функция D вычисляется в первый раз в начале поиска или же после вычисления функции качества (5) (алгоритм работал в допустимой зоне). В этом случае, когда D вычислена впервые, присваиваем D0 значение D (D0 = D) и переходим к этапу VI. Иначе рассчитываем новую величину шага по следующей формуле:

                (7)

Здесь У(Δ) – число удачных подряд шагов, δ(Δ) – целое, заранее известное число, определяющее количество удачных подряд шагов для увеличения величины шага, α(Δ) – коэффициент увеличения шага, α(Δ) > 1; Н(Δ) – число неудачных подряд шагов, χ(δ) – целое, заранее известное число, которое определяет число неудачных шагов для уменьшения шага, β(Δ) – коэффициент уменьшения шага, β(Δ) > 1; ε(Δ) – заданная точность, делать шаг меньше которой не имеет смысла; целое число r(Δ) определяет, сколько раз шаг уменьшался до заданной точности, если r(Δ) = l(Δ), которое задается заранее, то поиск прекращается, и точка Th принимается за оптимальную.

В случае, когда был получен удачный шаг (D < D0), значение Н(Δ) необходимо обнулить и перейти  к этапу VI; иначе, когда шаг получен неудачный (D ³ D0), необходимо обнулить У(Δ) и перейти к этапу IX.

При попадании в допустимую область поиска (этап V) обнуляется как У(Δ), так и Н(Δ). Для того чтобы достичь наибольшей надежности поиска, необходимо обнулять и r(Δ).

Этап IX. Здесь происходят возврат  в исходную точку по следующей формуле:

и переход на этап VI.

Этап X. После того как было получено новое значение функции качества F(Th), его необходимо сравнить с наилучшим значением, которые было занесено в память – F0. После этого формируется величина шага поиска в допустимой зоне.

В том случае, когда F(Th) > F0, считается, что шаг выбран удачно, и F0 необходимо изменить на значение F(Th); иначе шаг является неудачным, и F0 остается без изменения. В результате этого наилучшее значение F0 постоянно хранится в памяти.

Процедура формирования шага аналогична правилу (7):

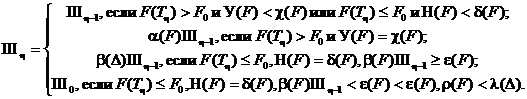
где все параметры имеют тот же смысл, что и в (7).

При получении удачного шага переходим к этапу VI, иначе к этапу IX. При r(F) =  l(F) в качестве оптимальной принимается точка (совокупность моментов начал всех операций задач в информационно-управляющей системе) tн(i, j), соответствующая F0, которая хранится в памяти вместе со значением T0.

Имея набор величин tн(i, j), соответствующих оптимальному технологическому процессу, и зная продолжительность всех работ – t(i, j), нетрудно рассчитать сроки окончания tо(i, j), и оптимальный план будет определен полностью.

Заключение

В статье предложены целочисленная модель и процедура формирования оптимального плана выполнения задач информационно-управляющей системы, реализующая метод случайного поиска с пересчетом с переменной величиной шага. Формируемый план задач информационно-управляющей системы представлен в виде сети. Предлагаемый подход позволяет получить оптимальный сетевой план задач информационно-управляющей системы в виде расписания начала времени выполнения задач системы, соответствующий минимальному времени выполнения всех задач информационно-управляющей системы и оптимальному использованию вычислительных ресурсов.

Рецензенты:

Бронов С.А., д.т.н., профессор, руководитель научно-учебной лаборатории систем автоматизированного проектирования кафедры систем искусственного интеллекта Сибирского федерального университета, г. Красноярск;

Ченцов С.В., д.т.н., зав. кафедрой «Системы автоматики, автоматизированное управление и проектирование» Сибирского федерального университета, г. Красноярск.