Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Для создания развитой образовательной среды необходимо значительное количество разнообразных тестов. Однако разработка тестов, в полной мере отвечающих требованиям теории IRT(ItemResponseTheory) [5], является весьма трудоемким процессом. Их разработка требует от учебного заведения больших временных и финансовых затрат. Вновь созданный тест, прежде чем быть допущенным к контрольным тестированиям, должен пройти стадию апробации. Только после достаточного количества пробных тестирований, проводимых на значительном количестве испытуемых, тест переводится в разряд корректных. Количество заданий в тесте также должно быть достаточно большим.

В то же время в процессе обучения постоянно требуется проведение текущего контроля небольших групп учащихся [2, 7], разработка тестов для которого вполне по силам небольшому преподавательскому составу. Особенно актуально это для интенсивно развивающегося в последнее время дистанционного образования, где количество тестируемых может быть равно одному [1, 8].

Постановка задачи

Рассмотрим кратко задачу статистической обработки результатов тестирования. Построим согласование оценок на основе одного часто используемого алгоритма обработки эмпирических данных современной теории тестирования с учетом специфики хранения и обработки знаний в системах автоматизации обучения. Будем также использовать методику и терминологию современной теории обработки тестирований IRT и достаточно известную модель Раша [6, 9].

Пусть в группе из  обучаемых проводится проверка успеваемости тестом, содержащим  заданий. Символ  обозначает результат выполнения i-м испытуемым j-го задания.

Вычисляются индивидуальные баллы каждого испытуемого  и каждого задания , как суммы правильно данных ответов

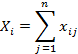
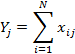
Предварительная оценка значений параметра , характеризующая уровень подготовки i-го ученика, вычисляется по формуле

(1)    

 — доля правильных ответов i-го ученика. Аналогично предварительная оценка значений параметра , характеризующая трудность j-го задания

 — доля правильных ответов на j-ое задание теста. После этого применяется дальнейшая обработка статистического тестового материала с использованием метода наибольшего правдоподобия. Составляется функция правдоподобия для i-го испытуемого

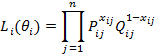(2)    

Где  — вероятность правильного выполнения i-м испытуемым j-го задания теста.  – вероятность неправильного выполнения i-м испытуемым j-го задания теста.  — результат выполнения задания 1 или 0. В качестве вероятностной функции берется функция конкретной модели IRT, например логистическая для однопараметрической модели Раша

Далее ищется значение , при котором функция правдоподобия достигает максимума. Это значение будет объективной оценкой искомого параметра. Его удобнее определять для логарифмической функции правдоподобия, решая следующее уравнение

Аналогично составляется функция правдоподобия для получения оценки  — уровня трудности j-го задания. И далее итерационным методом по очереди ищется решение этих систем, пока изменения оцениваемых параметров не станут меньше некоторого

Полученные таким способом значения оценок латентных переменных обладают свойствами нормального распределения и отражают взаимное расположение уровней подготовленности испытуемых и мер трудностей тестовых заданий на единой интервальной прямой. С помощью функций задающих плотности распределения вероятностей, например указанной выше функции Раша, по найденным значениям рассчитываются вероятности решения испытуемыми тестовых заданий.

Модификация алгоритма анализа данных

Использование цифровых технологий и автоматизированных систем в производстве позволяет усовершенствовать технологические процессы и приводит к их существенным качественным изменениям. В сфере образования значительный выигрыш приносит автоматизация контроля успеваемости в целом и результатов тестирований как его частной формы. При наличии достаточного количества вычислительной техники и соответствующего программного обеспечения проверка успеваемости проводится быстро и качественно. В современном образовании эти изменения в технологии образования оказываются весьма востребованными, так как позволяют быстро диагностировать появляющиеся проблемы и оперативно реагировать на них.

Регулярное проведение тестирований порождает процесс получения разнообразных данных. В дистанционном образовании он практически непрерывный. Для очной формы обучения тестирование имеет более дискретный характер, но, учитывая масштаб всего учебного заведения и необходимость отслеживания текущего и промежуточного контроля, данный процесс также можно рассматривать как непрерывный.

Каждое отдельное тестирование формирует набор характеристик. Из них основными являются оценки за тест, дополнительными – уровни сложности заданий, качество ответов, время выполнения и др. Некоторые характеристики относятся к конкретному тестированию, другие оказываются общими для многих тестирований. Некоторые подлежат точному измерению, другие имеют приближенный или оценочный характер. Исследуя процесс в динамике, можно оценивать погрешности, выявлять грубые ошибки измерений и отслеживать тренды. Ниже описано получение указанных показателей для произвольного параметра тестирования.

Будем рассматривать три последовательности: значения исследуемой случайной величины, взвешенные средние значения и весовые коэффициенты. Обозначим их . Начальные значения . На шаге  элементы последовательностей будут вычисляться по рекуррентным формулам

Соотношение (1) можно представить в другом виде

(3)    

Для взвешенного среднего значения ряда нормально распределенной случайной величины существует более 20 оценок. Предпочтительно использовать простое среднее, для которого

Эта оценка является состоятельной, несмещенной, эффективной и достаточной, использует весь массив статистической информации и является оценкой максимального правдоподобия. Стандартная ошибка среднего в этом случае

Ввиду возможных случайно возникающих грубых ошибок измерений некоторые значения  лучше не учитывать в общей сумме. Простейшим критерием выявления ошибки может служить сравнение текущего значения со среднеквадратическим отклонением .

Можно использовать либо теоретическое значение  либо с увеличением статистической информации по случайной величине вычислять оценочное значение

Оценка среднеквадратического отклонения будет приемлемой для .

Для отслеживания динамики некоторого показателя обычно используют диаграммы статистического контроля. Воспользуемся этим подходом и построим последовательности нарастающих сумм:  – для отслеживания тенденции роста,  – для отслеживания тенденции снижения, . Элементы последовательностей определяются на каждом шаге:

Положим . При превышении величин некоторого заданного порогового значения  можно утверждать, что обнаруживается устойчивый тренд к изменению средневзвешенного значения ряда

Другие полезные динамические характеристики: статистическое отклонение из (3),  и сдвиг средневзвешенной суммы (2), .

В последнем случае вместо константы  нужно использовать асимптотическую функцию вида . Превышение порога укажет тренд и смещения, и разброса значений.

Заключение

Предложенный алгоритм анализа данных результатов тестирований и отслеживания динамики с помощью накопленных сумм обладает преимуществами простоты компьютерной реализации и устойчивостью. Этот алгоритм может  применяться в системах по контролю и оценке знаний и компетенций в процессе обучения [3]. Использование указанного алгоритма в автоматизированной системе поддержки образовательного процесса позволит осуществлять непрерывный контроль [4] и существенно повышать характеристики качества образовательного процесса.

Рецензенты:

Майков К.А., д.т.н., профессор кафедры программного обеспечения ЭВМ и информационных технологий МГТУ имени Н.Э.Баумана, г. Москва;

Николаев А.Б., д.т.н., профессор, декан факультета «Управление», заведующий кафедрой «Автоматизированные системы управления» ФГБОУ ВПО «Московский автомобильно-дорожный государственный технический университет (МАДИ)», г. Москва.