Цель исследования
Теоретическое обоснование предлагаемых технических решений для осуществления сбора древесины в береговой зоне водохранилищ, и доставки её в прибрежную акваторию и дальнейшей транспортировке потребителям.
Материал и методы исследования
На первом этапе проведён анализ влияния геометрических параметров системы для сбора древесины (длина пролета l, разность высот закрепления несущего каната h), параметров каната (погонный вес q и жесткостные свойства), веса пачки лесоматериалов P на усилия, возникающие в точках закрепления канатов и непосредственно в самом канате, а также на провис несущего каната. По результатам получены зависимости, связывающие указанные параметры в статике. Они являются основой анализа влияния скорости перемещения пачки лесоматериалов на усилия в системе и провис каната (решение задачи динамики). Использование полученных оценок усилий позволит провести обоснование параметров устройств, отвечающих за крепление плавучей платформы устройства для сбора древесины (на которой размещена одна из мачт).
Ввиду сложности математического описания работы несущего каната под действием переменных динамических нагрузок, при выполнении исследований использовались численные методы решения и аппроксимации расчетных данных.
В проводимых исследованиях ориентировались на характеристики стальных канатов, представленные в ГОСТ 2688.80 «Канаты стальные. Сортамент». В таблице 1 представлены значения регламентированных ГОСТ 2688.80 «Канаты стальные. Сортамент» значений диаметров dK [мм], ориентировочных масс 1000 м каната mK [кг] и рассчитанных по их значениям погонных весов q [Н/м] канатов, а также площадей поперченных сечений проволок канатов S [мм2]. Численные расчеты осуществляли в прикладной программе Maple 14, образовательная версия. В итоге получили следующие выражения (на примере маркировочной группы 1370 Н):
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
Сходимость выражений (1) – (3) со справочными данными видна из графиков на рисунке1 и график служит также для более наглядного представления зависимостей указанных величин от диаметров стальных канатов. ГОСТ 2688.80 «Канаты стальные. Сортамент» предусматривает следующие маркировочные группы стальных канатов (по разрывному усилию на 1 мм2 площади поперечного сечения): 1370 Н, 1470 Н, 1570 Н, 1670 Н, 1770 Н, 1860 Н, 1960 Н, 2060 Н, 2160 Н. Важно отметить, что зависимости (1) – (3) остаются практически неизменными при варьирования маркировочной группы каната. ГОСТ 2688.80 «Канаты стальные. Сортамент» не содержит необходимых данных о модулях упругости канатов, поэтому использовали справочные данные, для оценки характеристик стальных конструкций, которые содержатся в СНиП II–23–81 «Стальные конструкции». Опираясь на них и формулу (3), получили выражение для расчета жесткости стальных канатов при растяжении:
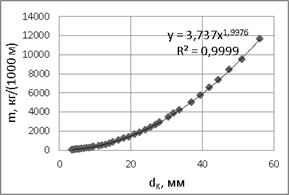
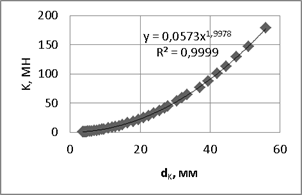
Рис.1. Зависимость массы 1000 м каната Рис. 2 Ориентировочная жесткость
от диаметра стального каната стальных канатов в зависимости от диаметра
![]() (4)
(4)
В этом случае оценить величину жесткости канатов в зависимости от диаметра можно также с использованием графика, представленного на рисунке 2.
При необходимости учесть нелинейный характер связи модуля упругости и относительной деформации растяжения каната, следует учитывать, что жесткость на растяжение K будет являться переменной величиной, зависящей от удлинения каната. Получить зависимости жесткости от диаметра каната и величины удлинения возможно при наличии дополнительных экспериментальных данных по испытаниям стальных канатов на растяжение.
Расчет усилий и провисания каната (статическая нагрузка)
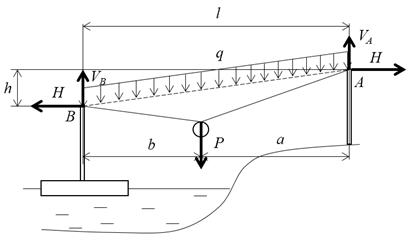
Рис.3. Расчетная схема к определению провиса каната
при перемещении груза
Из схемы на рисунке 3 следует система уравнений равновесия, решение которой позволяет определить значения вертикальных составляющих реакций в точках крепления каната:
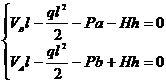 (5)
(5)
где l – длина пролета, a, b – расстояния груза от левой и правой опор соответственно, H – горизонтальная составляющая реакции в точках крепления каната (распор), h – разность высот точек крепления каната.
Из решения системы уравнений (5) получим для реакций VA, VB следующие зависимости:
![]() (6)
(6)
![]() (7)
(7)
Поперечную силу Q(x) в зависимости от координаты поперечного сечения каната найдем по формуле:
![]() (8)
(8)
где He(ξ) – единичная функция Хевисайда, ξ – аргумент единичной функции Хевисайда (в формуле (8) ξ = x – b), причем единичную функцию Хевисайда определим следующим образом:
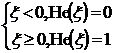 (9)
(9)
После подстановки выражения для VA по формуле (6) в выражение (8) для поперечной реакции Q получим:
![]() (10)
(10)
Поскольку канат практически не сопротивляется изгибу, а по условию равновесия изгибающий момент M(x) в любом его сечении равен нулю, запишем следующее равенство:
![]() (11)
(11)
Или иначе:
![]() (12)
(12)
Продифференцируем выражение (12) по x, тогда получим следующую зависимость:
![]() (13)
(13)
Поскольку производная изгибающего момента по координате x является поперечной силой Q:
![]() (14)
(14)
Выражение (13) перепишем следующим образом:
![]() (15)
(15)
Под действием собственного веса и веса груза P канат принимает форму кривой S, длина которой находится по известной зависимости:
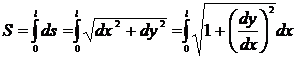 (16)
(16)
С учетом формулы (15), уравнение (16) представим в следующем виде:
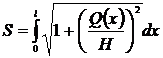 (17)
(17)
Выражение для длины кривой S по формуле (17) можно разложить в ряд по [8-9] с целью упростить последующие вычисления, тогда:
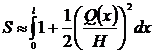 (18)
(18)
Последнее выражение запишем следующим образом:
![]() (19)
(19)
Для упрощения записи перепишем зависимость (19) следующим образом:
![]() (20)
(20)
где использовано обозначение:
![]() (21)
(21)
Подставим выражение для поперечной силы Q(x) по формуле (10) в зависимость (21):
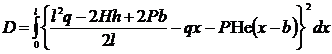 (22)
(22)
После интегрирования по [8-10] формулы (22) получим общее выражение в следующей форме:
![]()
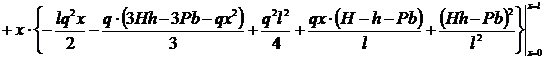 (23)
(23)
Окончательно для вспомогательной величины D получим следующее выражение:
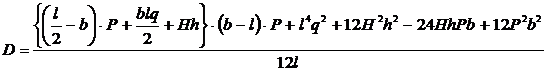 (24)
(24)
Начальная длина каната (без нагрузки) определяется в соответствии со схемой на рисунке 3 по формуле:
![]() (25)
(25)
Относительная деформация растяжения каната ε под действием нагрузки связана с распором H и жесткостью каната K следующей зависимостью:
![]() (26)
(26)
Поскольку:
![]() , (27)
, (27)
из формулы (26) получим следующее выражение:
![]() (28)
(28)
Выражения (20), (25), (28) в совокупности образуют уравнение относительно распора H:
![]() (29)
(29)
где вспомогательная величина D определяется по формуле (24).
При заданных значениях l, h, K, P, b, q уравнение (29) решается относительно величины H.
При выводе уравнения изогнутой линии каната под действием нагрузки необходимо учесть разность высот точек его закрепления. В связи с этим перепишем уравнение (9), описывающее равновесие каната, в следующем виде:
![]() (30)
(30)
С учетом выражения (8) для поперечной силы Q(x) получим:
![]() (31)
(31)
где δ(x – b) – дельта–функция Дирака [10].
Общее решение уравнения (30) имеет следующий вид [10]:
![]() (32)
(32)
Для определения постоянных C1 и C2 (обеспечивающих учет особенностей закрепления концов каната на разной высоте) воспользуемся начальными условиями, которые следуют из расчетной схемы на рисунке 3. В этом случае:
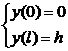 (33)
(33)
При начальных условиях по выражению (33), после совместного решения уравнений (32), (33) получим выражения для постоянных C1 и C2:
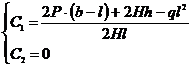 (34)
(34)
Тогда решение уравнения (32) примет вид:
![]() (35)
(35)
При этом вертикальное перемещение каната под действием собственного веса и веса груза (провис каната) рассчитаем по следующей зависимости:
![]() (36)
(36)
где y0 – вертикальная координата сечения каната без нагрузки.
Таким образом, уравнения (6), (7), (24), (29), (35), (36) позволяют определить реакции в точках закрепления каната VA, VB, H (что необходимо при расчете крепления плавучего основания и береговой мачты) и провис каната f.
Анализ расчетных данных показал, что наибольшая величина провиса отмечается при нахождении груза в середине пролета, т.е. при β = 0,5l. Величину провиса в этом случае обозначим f(0,5), форма изогнутой оси каната является характерной при всех сочетаниях исходных данных для расчета.
Аппроксимация полученных расчетных данных позволила получить многопараметрическую функцию для оценки провиса каната при нахождении груза в середине пролета (т.е. максимального значения), выраженного в процентах от длины пролета, при варьировании массы груза G (т), диаметра каната dK (мм), угла наклона каната φ (град):
![]() (37)
(37)
Далее аппроксимировали полученные расчётные данные и получили по аналогии многопараметрическую функцию для оценки распора при варьировании массы груза G (т), диаметра каната dK (мм), угла наклона каната φ (град) (влияние прочих факторов можно считать несущественным):
![]() (38)
(38)
Заключение
Уравнения (37) и (38), полученные для расчета провиса несущего каната и распора, служат основой для исследований динамических реакций, расчет которых позволит уточнить составляемую математическую модель и расширить спектр ее применения – путем учета важного технологического параметра процесса доставки древесины с берега в воду или на плавучее основание, или наоборот, на берег, а именно – скорости перемещения пачки лесоматериалов, определяющей (наряду с весом и объёмом), производительность.
Рецензенты:Иванов В.А., д.т.н., профессор, заведующий кафедрой воспроизводства и переработки лесныхресурсов, Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Братский государственный университет», г. Братск;
Гаспарян Г.Д., д.т.н., доцент, декан Лесопромышленного факультета Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Братский государственный университет», г. Братск.
Библиографическая ссылка
Жук А.Ю. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РАБОТЫ УСТРОЙСТВА ДЛЯ СБОРА И ТРАНСПОРТИРОВКИ ДРЕВЕСИНЫ В БЕРЕГОВОЙ ЗОНЕ ВОДОХРАНИЛИЩ ПРИ СТАТИЧЕСКОЙ НАГРУЗКЕ, ДЕЙСТВУЮЩЕЙ НА НЕСУЩИЙ КАНАТ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=19087 (дата обращения: 03.03.2026).



