Пути в графе определяются функцией WAYS(G;PQ;C), аргументами которой являются: структурная строка графа (G), начальная (P) и конечная (Q) вершины пути, тип графа (С). При С = 0 орграф, при С = 1 реберный. Структурная строка графа имеет вид:
G = A12 B31 C23 D42 E34. (1)
Структурная строка G состоит из троек символов, соответствующих ребрам (дугам) графа. На 1-м месте в тройке находится имя дуги, на 2-м и 3-м местах — начальная и конечная вершины дуги. Дуги и вершины имеют односимвольное обозначение. Дуги обозначаются большими буквами, вершины — цифрами и буквами. При количестве вершин более 9 они обозначаются большими буквами латинского и русского алфавитов. Если вершины обозначаются буквами, строка PQ берется в кавычки. В данном примере функция WAYS для реберного графа выдает пути между вершинами 1 и 4:
WAYS =WAYS(C44;14;1). (2)
Для орграфа
WAYS = =WAYS(C44;14;0). (3)
Кроме функции WAYS, в данной программе имеются функции, определяющие контуры графов, длины путей, пропускные способности путей, пути минимальной длины, пути, проходящие через все вершины графа, гамильтоновы циклы и другие функции, применяемые для решения различных задач на графах. К таким задачам относятся, например, определение максимальных потоков, потоков минимальной стоимости, транспортные задачи, систем управления и планирования (СПУ), задачи коммивояжера, задачи о назначении персонала, вероятностный анализ графов, анализ решений систем уравнений, задачи составления расписаний и др. Примеры решения подобных задач рассматриваются ниже.
Выбор пути минимальной длины
Формулировка задачи: дана схема дорог, связывающих пункт отправления и пункт назначения. Требуется определить маршрут минимальной длины, связывающий эти пункты. Некоторые дороги имеют одностороннее движение.
Решение
Схема дорог и их длины задаются таблицей графа, приведенной ниже. Схема дорог представлена на рисунке 1.

Рис. 1. Схема дорог
Граф на рисунке 1 представляется следующей таблицей 1.
Таблица 1
Данные к задаче выбора пути минимальной длины
|
N=10 |
41 |
12 |
13 |
23 |
35 |
26 |
74 |
65 |
57 |
67 |
|
Длина |
40 |
26 |
30 |
20 |
25 |
20 |
30 |
20 |
15 |
20 |
|
Ребро |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
Таблица содержит в 1-м столбце номера начальных и конечных вершин ребер, во 2-м столбце — количество ребер и их длины. Набор допустимых путей от вершины P к вершине Q с учетом одностороннего движения по некоторым дорогам определяется функцией WaysArc(AT;PQ;SA), где АТ — адрес таблицы графа, SA — строка набора ориентированных дуг, соответствующих дорогам с односторонним движением. Направление этих дуг определяется в таблице начальными и конечными их вершинами. Для приведенного на рисунке 1 графа ориентированными дугами являются дуги D и H. Если ориентированных дуг нет, аргумент SA = "". В данном примере функция WaysArc при PQ = 17 выдает следующий результат (набор возможных путей между вершинами 1 и 7):
WaysArc("B96";17;"DH"). (5)
Пути минимальной длины можно выделить из набора (4) допустимых путей функцией MinWaysArc(SW;AT;PQ;Pr), аргументами которой являются набор допустимых путей (4), адрес таблицы графа, начальная и конечная вершины пути, массив влияющих параметров (массив длин дорог в таблице графа). В данном случае функция выдает следующий результат:
MinWaysArc(B120;"B96";17;C97:C106). (6)
Определить длину каждого пути можно функцией LenPath(W;AT;MP), пропускную способность — CapacityWay(AT;W;MP).
Определить минимальный путь можно и функцией MinWaysOr(AT;PQ;SA;P). Эта функция не требует предварительного определения всех путей, но работает медленнее. Для данного графа результаты ее работы при SA = "" таковы:
MinWaysOr("B96";17;"";C97:C106). (8)
Если граф чисто реберный или ориентированный, минимальные пути можно найти функцией MinWays(AT;PQ;C), где аргумент С определяет тип графа: при С = 0 граф ориентированный, иначе реберный. Результаты работы этой функции при определении минимального пути от вершины 7 к вершине 1 следующие:
MinWays("B96";71;1) <для реберного графа,
MinWays("B96";71;0) <для орграфа. (9)
Ориентация дуг в орграфе определяется таблицей графа: дуга, обозначаемая в 1-м столбце символом "ij", направлена от вершины i к вершине j.
Определение пропускных способностей путей
Путь состоит из последовательности дорог. Каждая дорога имеет свою пропускную способность. Поэтому пропускная способность пути определяется пропускной способностью одной из дорог, которая входит в путь. Пропускная способность пути W определяется функцией CapacityWay(AT;W;MP), аргументами которой являются адрес таблицы графа, путь W, массив влияющих параметров (MP) (пропускные способности дорог во 2-м столбце таблицы (4)). Путь минимальной пропускной способности определяется функцией MinCapW(AT;PQ;C; MP). Путь максимальной пропускной способности определяется функцией MaxCapW(AT;PQ;C;MP). Для графа на рисунке 2 эти функции для реберного графа (С = 1,PQ = 17) дают следующие результаты:
MinCapW = MinCapW("B96";17;1;C97:C106), MaxCapW = MaxCapW("B96";17;1;C97:C106). (10)
В строках (10) последняя подстрока определяет длину пути, т. е. минимальная пропускная способность путей определяется ребром B, а максимальная пропускная способность определяется весом ребра A. Значит, чтобы увеличить пропускные способности 4 путей, достаточно увеличить пропускную способность дороги, обозначенную ребром В. Однако увеличение пропускной способности В увеличивает пропускные пути незначительно, и не имеет смысла увеличивать пропускную способность дороги В более чем на одну единицу пропускной способности, т.е. более чем на 7%. Кроме функций (10), имеются еще две функции: MinWayWA(AT,PQ,SA,MP), MaxWayWA(AT,PQ,SA,MP). Примеры их применения: при наборе ориентированных ребер SA = "DH" и PQ = 17 для графа (4) получаем:
MinCapWA = MinCapWA("B96";17;"DH";C96:C106),
MaxCapWA = MaxCapWA("B96";17;"DH";C96:C106). (11)
Эти функции можно применять для полностью реберных графов и для полностью ориентированных графов. В 1-м случае SA = "", во 2-м случае SA включает все ребра графа. Для графа (4) SA = ABCDEFGHIJ Соответственно, при значении функций (11) для реберного графа будут такими:
MinCapWA = MinCapWA("B96";17;"";C97:C106), MaxCapWA = MaxCapWA("B96";17;"";C97:C106), (12)
для орграфа:
MinCapWA = MinCapWA("B96";17;C190;C97:C106),
MaxCapWA = MaxCapWA("B96";17;C190;C97:C106). (13)
Полные пути, деревья, контуры, гамильтоновы циклы
Полным путем является не самопересекающийся путь, содержащий все вершины графа. Такой путь имеется не между любыми парами вершин и не в любом графе. Полный путь между вершинами P и Q определяется функцией TotalWays(G;PQ;C) по структурной строке G графа, где С определяет тип графа (С = 0 для орграфа и С = 1 для реберного графа). Структурная строка G графа определяется функцией StrStrGLV(AT) по таблице графа. Для графа на рисунке 2 с таблицей (4)
G = StrStrGLV("B96"). (14)
Примеры использования функции TotalWay для графа (14):
W(14) = TotalWays(B211;14;1), W(17) = TotalWays(B211;17;1), W(12) = TotalWays(B211;12;1). (15)
Другим типом подграфа, содержащим все вершины графа и не содержащим контуров (замкнутых путей), является дерево. В дереве между любой парой вершин существует единственный путь. Деревья определяются функцией TreesG(G). Набор деревьев минимального веса определяется функцией MinTrees(AT;MP). Для графа (4) функция выдает:
MinTrees("B96";C97:C106). (16)
Количество ребер дерева на 1 меньше количества вершин графа. Любое ребро, не входящее в дерево, при его возврате в состав дерева образует один контур. Количество контуров, соответствующих любому дереву, одно и то же и равно разности между общим количеством ребер, входящих в контуры, и количеством ребер дерева. Количество ребер графа, не входящих в контуры, определяется функцией BRIDGES(G). Такие ребра при их исключении разбивают граф на два подграфа, не имеющих общих вершин. Например, для графа, представленного структурной строкой G = A12 B23 C24 D43 E35 F56 G57 H76 I68 (17) и изображенного на рисунке 2, функция BRIDGES выдает:
BRIDGES = BRIDGES(B233). (18)
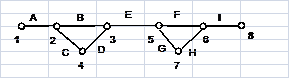
Рис. 2. Неориентированный граф
Удаление любого из этих трех ребер разделяет граф на две несвязанные части. Кроме деревьев, содержащих все вершины графа, имеется понятие подграфа, называемого покрытием. Такой подграф, так же как и дерево, содержит все вершины графа и не содержит ни одного контура. Покрытие подграф состоит из несвязанных частей, имеющих максимальную длину путей не более чем из 2 ребер. Вариантов такого разбиения довольно много. Наибольший интерес представляют минимальные покрытия, т.е. покрытия, состоящие из наименьшего возможного количества ребер. Минимальные покрытия определяются функцией MnCovers(G). Для графа на рисунке 2 минимальным покрытием является следующий набор ребер:
MnCovers = MnCovers(B233). (19)
Контуры графа определяются функциями ContRibG(G) и ContArcG(G) соответственно для реберных и графов. Для графа на рисунке 2 контуры орграфа следующие:
ContArcG(B211). (20)
Для графов на рисунках 1 и 2 реберные контуры такие:
ContRibG(G1) = ContRibG(C44), (21)
ContRibG(G3) = ContRibG(B233).
Контуры, содержащие все вершины графа, называются гамильтоновыми циклами и определяются функцией GamCyc(G;C). C определяет тип графа (С = 0 орграф, С = 1 реберный). Для графа на рисунке 2 функция GamCyc при С = 1 выдает:
GamCyc = GamCyc(B211;1). (22)
С определением гамильтоновых циклов связана задача коммивояжера. Она заключается в определении оптимального маршрута объезда всех пунктов с посещением каждого из них только один раз. Решается эта задача выбором из всех гамильтоновых циклов наиболее короткого или оптимального в смысле стоимости проезда. Для этого используется функция MinGamCyc(GC;AT;MP), выбирающая из набора GC гамильтоновых циклов цикл минимальной длины. Так, эта функция из набора (22) выдает:
MinGamCyc(C270;"B96";C97:C106). (23)
Группы несмежных вершин
Задачу определения групп несмежных вершин можно трактовать как задачу составления расписаний. Вершины графа имеют признаки общности. Например, вершине можно сопоставить занятие группы с определенным преподавателем и в определенном списке аудиторий. Если вершины имеют общие параметры, они связаны друг с другом и, стало быть, несовместимы. Требуется найти группы совместимых вершин, т.е. не связанных между собой ребрами. Рассмотрим эту задачу на примере графа на рисунке 3.
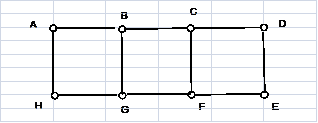
Рис. 3. Граф задачи определния групп несмежных вершин
Требуется распределить вершины по группам, в которых вершины не имеют взаимных связей. Для решения задачи используется функция GrpNcrTops(G).
Функцией StrStrGLV(AT) получаем структурную строку графа:
StrStrGLV("C311"). (25)
По строке (25) функцией GrpNcrTops получаем группы не связанных между собой ребрами вершин:
GrpNcrTops(A323). (26)
Рассмотрим способ составления расписаний учебных занятий на простом примере. Задача получения списков совместных (единовременных) занятий сводится к задаче определения несмежных вершин графа, отображающего взаимосвязи между занятиями, (вершинами графа). Каждое занятие представляется набором (записью) составляющих, который включает преподавателя, группы, с которыми занимается преподаватель, и аудиторию, в которой проходят занятия. Записи компонуются из списка преподавателей, групп или подгрупп (для лабораторных занятий), групп аудиторий, которые могут быть использованы для соответствующих видов занятий (лекционных, практических, лабораторных). Когда записи сформированы, их совокупность и взаимосвязь представляются реберным графом, в котором вершины соответствуют записям (занятиям), а ребра, соединяющие вершины, означают наличие общих элементов в записях, т.е. несовместимость занятий, соответствующих вершинам, соединяемым ребром. В нижеприведенной таблице 2 представлен набор записей, соответствующих различным видам занятий.
Таблица 2
Набор записей, соответствующих различным видам занятий
|
№ зан. |
Преподаватель |
Вид занятий |
Группы |
Аудитории |
||
|
E F |
G H |
P Q |
R S T |
|||
|
A |
A |
лк. |
* * |
* |
||
|
B |
B |
лк. |
* * |
* |
||
|
C |
A |
пр. |
* |
* |
||
|
D |
A |
лб. |
* |
* |
||
|
E |
B |
пр. |
* |
* |
||
|
F |
B |
лб. |
* |
* |
||
|
G |
C |
пр. |
* |
* |
||
|
H |
C |
пб. |
* |
* |
||
|
I |
D |
пр. |
* |
* |
||
|
J |
D |
лб. |
* |
* |
||
Таблица содержит информацию о виде каждого занятия и о месте его проведения, о количестве преподавателей и учебных групп студентов. Имеется одна аудитория лекционная (P), две аудитории для практических занятий (Q,R) и две для лабораторных занятий (S,T). Всего должно быть 10 занятий, т.е. соответствующий граф содержит 10 вершин, ребра графа определяются по факту наличия общих преподавателей, учебных групп и аудиторий в различных записях, т.е. наличие звездочек хотя бы в одном столбце у двух записей означает их несовместимость и, следовательно, наличие ребра между соответствующими вершинами.
Структурная строка графа, представляющего таблицу 2, будет такой:
StrStrGLV("B372").
По этой строке функцией GrpNcrTops(G) получаем списки совместимых по времени занятий:
GrpNcrTops(A393). (28)
Расписание может быть представлено следующей таблицей 3.
Таблица 3
Расписание занятий
|
|
|||
|
Пары |
Лекции |
Практические |
Лабораторные |
|
1 |
BGHP |
CFQ |
AES |
|
2 |
AEFP |
DHR |
BGT |
|
3 |
BGR,DHR |
AEQ,CFS |
|
В строке (28) буквы обозначают занятия согласно 1-му столбцу таблицы 2. В таблице 3 буквы обозначают: на 1-ой позиции преподаватели, на последней позиции аудитории, между ними обозначения групп.
Рецензенты:Славутский Л.А., д.ф.-м.н., профессор кафедры автоматики и управления в технических системах (ФГБОУ ВПО «ЧГУ им. И.Н. Ульянова»), г. Чебоксары;
Охоткин Г.П., д.т.н., профессор, заведующий кафедрой автоматики и управления в технических системах (ФГБОУ ВПО «Чувашский государственный университет имени И.Н. Ульянова»), г. Чебоксары.
Библиографическая ссылка
Музыкантов В.И., Желтов В.П. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ЗАДАЧ НА ГРАФАХ В ЕХCEL // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=19062 (дата обращения: 12.03.2026).



