Анализ факторов, влияющих на уровень инновационного развития отрасли, позволяет спрогнозировать динамику колебаний соотношения различных показателей.
Математическим аппаратом модели прогнозирования является теория нечеткой логики, позволяющая формализовать причинно-следственные связи между входными и выходным переменными. Эти связи определяются с помощью специалистов (экспертов) в данной области знаний и составляют базу знаний в модели прогнозирования. На основе созданной таким способом базы знаний предлагается осуществлять моделирование и прогнозирование уровня инновационного развития отрасли.
Построение модели прогнозирования уровня инновационного развития отрасли на основе нечеткой логики целесообразно осуществлять на основе следующих принципов [1]:
1) принципа лингвистичности переменных модели (определенные входящие и исходящие параметры модели рассматриваются как лингвистические качественные переменные);
2) принципа лингвистичности высказываний (выводов) при принятии конкретных решений. Причинно-следственные связи между входящими и исходящими параметрами модели описываются словестно (вербально), а затем формализуются в виде совокупности нечетких логических высказываний (выводов) типа: «если – то», «иначе» и т. п.;
3) принципа иерархичности лингвистических высказываний (заключений);
4) классификации входящих переменных (параметров) модели и построения «дерева» вывода, которое является системой вложенных друг в друга высказываний (выводов, знаний) экспертов «меньшей размерности». Это позволяет избежать трудностей, связанных с анализом и формализацией большого количества входных переменных (параметров). Соблюдение этого принципа позволяет учитывать практически неограниченное количество входных переменных, влияющих на формирование инновационного потенциала отрасли.
Таким образом, построение модели прогнозирования уровня инновационного развития отрасли на основе использования теории нечеткой логики можно свести к таким этапам, как [2]:
1) определение четких и нечетких входящих переменных (параметров) модели или получения лингвистических высказываний (заключений) экспертов;
2) построение дерева вывода;
3) определение границы изменения входящих переменных (параметров);
4) оценки лингвистических высказываний экспертов, которые принимаются за входящие переменные (параметры) модели;
5) создание базы знаний;
6) формализация базы знаний в виде нечетких логических высказываний (выводов);
7) построение системы нечетких логических уравнений;
8) выбор метода построения функций принадлежности, которые обеспечат представление количественных и качественных переменных (параметров) в виде нечетких множеств для лингвистических термов, входящих в базу знаний [4].
В нечеткой базе знаний каждая строка является нечетким правилом, которое представляет собой высказывание типа «если — то». Нечеткие правила, имеющие одинаковый исходящий параметр, объединяются между собой в уравнение с помощью слова «и».
Для получения нечеткого логического выражения (заключения) необходимо осуществить переход от лингвистических высказываний в нечеткие логические уравнения. Результатом решения системы нечетких логических уравнений является нечеткий логический вывод (совокупность значений функций принадлежности исходящего параметра модели). Переход от полученной совокупности значений функций принадлежности к значению прогнозного выходного параметра осуществляется с помощью операции дефазификации. Дефазификация представляет собой обратное преобразование найденного нечеткого логического выражения (заключения) в выходной прогнозный параметр (переменную), подлежащий моделированию и прогнозированию.
Рассмотрим процесс построения нечетких высказываний и определение уровня инновационного развития на примере.
Обозначим все входящие переменные следующим образом:
Z = fz (х1, х2, х3, х4, х5) – профессионально-квалификационный потенциал;
M = fm (х6, х7, х8) – состояние финансового потенциала;
N = fn (х9, х10, х11) – состояние интеллектуального потенциала;
Y = fy (х12, х13, х14, х15) – состояние информационной среды;
W = fw (х16, х17, х18, х19) – состояние инфраструктуры;
V = fv (х20, х21, х22) – состояние производственной среды;
L= fl (х23, х24, х25, х26) – управление производственным процессом;
H = fh (х27, х28) – состояние ресурсного потенциала;
T = ft (х29) – период прогнозирования;
D = fd (z, ….., t) – прогнозируемый уровень инновационного развития отрасли.
На рисунке 1 представлен граф структуры модели прогнозирования уровня инновационного развития, в котором показывается зависимость между входящими и выходным показателем модели. Для упрощения процесса построения модели сведем дополнительные обобщенные лингвистические исходные параметры.
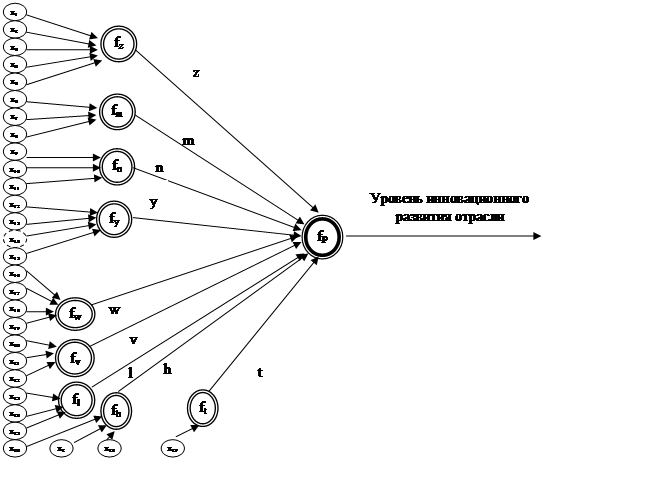
Рис. 1. Дерево логического вывода оценки уровня инновационного развития отрасли
При построении модели прогнозирования уровня инновационного развития отрасли будем использовать входные количественные и входные качественные одновременно для описания входных параметров {x1. . . x4, x6. . . x11}, которые являются количественными, могут использоваться официальные статистические данные, для описания других входных параметров, кроме {x29}, которые являются качественными, можно использовать условную балльную шкалу оценок от «0» до «100» баллов. Для входной переменной x23 введем термы 1, 2, 3 года соответственно периодам прогнозирования.
Таким образом, полученная структура модели оценки уровня инновационного развития отрасли показывает, что эта модель фактически содержит в себе восемь моделей:
1) модель зависимости уровня инновационного развития от уровня квалификационных факторов;
2) модель зависимости уровня инновационного развития от финансовых показателей;
3) модель зависимости уровня инновационного развития от состояния информационной среды;
4) модель зависимости от производственных условий;
5) модель зависимости от состояния инфраструктуры;
6) модель зависимости от управленческих воздействий;
7) модель зависимости от ресурсного потенциала;
8) модель зависимости от интеллектуального потенциала.
В таблице 1 приведены термы, используемые для лингвистической оценки этих переменных, их диапазонов.
Входные переменные модели и их лингвистическая оценка
|
З. |
Показатели |
Значения |
Термы |
|
1 |
2 |
3 |
4 |
|
Х1 |
Профессиональное продвижение
|
0…100 |
очень низкий (ДН); средний (С); стабильный (СТ); выше среднего (ВС); высокий (В). |
|
……………………………………………………………………………………………… |
|||
|
Х29 |
Прогноз |
1…1000 дней |
1 год (1Д); 2 года (2Д); 3 года (3Д). |
Для оценки значений обобщенных исходных параметров {Z, M, N, Y, W, V} будем использовать шкалу оценок от «0» до «100» баллов. Для переменной «прогнозирование» Х29 введем термы, соответствующие диапазонам составлении прогноза: 1–3 года (краткосрочное прогнозирование). При этом введем следующие обозначения: низкий (Н), ниже среднего (НС), средний (С), выше среднего (ВС), высокий (В) уровень обобщенного исходящего параметра. Определяем также характерные уровни изменения главного исходящего параметра D, подлежащего прогнозированию. Возможные значения уровня инновационного развития обозначим следующими уровнями: d1 – уровень инновационного развития выше среднего (80–100%), d2 – средний уровень инновационного развития (67–80%), d3 – уровень инновационного развития ниже среднего (37–67%), d4 – низкий уровень инновационного развития (20–37%), d5 – абсолютное отсутствие инноваций (0–20%). Приведенные уровни будем считать качественными характеристиками, которые определяют изменение уровня инновационного развития.
Рассмотрим базу знаний и нечеткие логические высказывания.
Входные переменные: fz — уровень профессионально-квалификационного потенциала (Н, НС, С, ВС, В); fm – состояние финансового потенциала (Н, НС, С, ВС, В); fn — уровень интеллектуального потенциала (Н, НС, С, ВС, В); fу — уровень производственных параметров (Н, НС, С, ВС, В); fw – состояние инфраструктуры (Н, НС, С, ВС, В); fv – состояние производственной среды (Н, НС, С, ВС, В); fl – состояние производственных процессов (Н, НС, С, ВС, В); fh – состояние ресурсного потенциала (Н, НС, С, ВС, В); t — уровень периода прогнозирования (1М, 2М, 3М). Входные переменные при формировании правил системы нечеткого вывода связаны функцией конъюнкции (нечеткое логическое И).
Выходная переменная: d — уровень инновационного развития отрасли (d1 – уровень инновационного развития выше среднего, d2 — средний уровень инновационного развития, d3 – уровень инновационного развития ниже среднего, d4 – низкий уровень инновационного развития, d5 – абсолютное отсутствие инноваций).
Таблица 2
Правила системы нечеткого вывода d
|
|
fz |
fm |
fn |
fу |
fw |
fv |
fl |
fh |
t |
|
d |
|
Если |
НС |
НС |
НС |
НС |
НС |
НС |
Н |
С |
2Д |
то |
d1 |
|
Если |
С |
С |
С |
С |
С |
С |
ВС |
Н |
3Д |
то |
d1 |
|
Если |
Н |
Н |
Н |
Н |
Н |
Н |
С |
НС |
1Д |
то |
d1 |
|
Если |
С |
С |
С |
С |
С |
С |
С |
С |
3Д |
то |
d2 |
|
Если |
ВС |
НС |
НС |
ВС |
НС |
НС |
ВС |
ВС |
2Д |
то |
d2 |
|
Если |
НС |
В |
В |
НС |
В |
В |
В |
ВС |
1Д |
то |
d2 |
|
Если |
ВС |
ВС |
ВС |
ВС |
ВС |
ВС |
С |
НС |
1Д |
то |
d3 |
|
Если |
ВС |
С |
С |
ВС |
С |
С |
С |
С |
3Д |
то |
d3 |
|
Если |
С |
В |
В |
С |
В |
В |
НС |
ВС |
2Д |
то |
d3 |
|
Если |
ВС |
В |
В |
ВС |
В |
В |
С |
ВС |
1Д |
то |
d4 |
|
Если |
ВС |
ВС |
ВС |
ВС |
ВС |
ВС |
НС |
С |
2Д |
то |
d4 |
|
Если |
В |
С |
С |
В |
С |
С |
Н |
НС |
3Д |
то |
d4 |
|
Если |
В |
В |
В |
В |
В |
В |
НС |
В |
1Д |
то |
d5 |
|
Если |
В |
С |
С |
В |
С |
С |
Н |
С |
3Д |
то |
d5 |
|
Если |
В |
В |
В |
В |
В |
В |
Н |
ВС |
2Д |
то |
d5 |
Сформируем нечеткие логические выражения:
ЕСЛИ [z = НС] и [y = НС] и … и [t = 1Д] ТО d = d1.
ЕСЛИ [z = С] … и [t = 3М] И [z = ВС] и [y = НС] и … и [t = 1Д] ТО d = d2.
ЕСЛИ [z = ВС] и … и [t = 2Д] ТО d = d3.
ЕСЛИ [z = ВС] и [y = В] и … и [t = 3Д] ТО d = d4.
ЕСЛИ [z = В] и … и [t = 2Д] ТО d = d5.
Программная реализация модели прогнозирования осуществлена в среде MATLAB. Нечеткое моделирование в среде MATLAB осуществляется с использованием расширения Fuzzy Logic Toolbox, в котором реализованы десятки функций нечеткого вывода и нечеткой логики (рис. 2, 3) [3, 5].
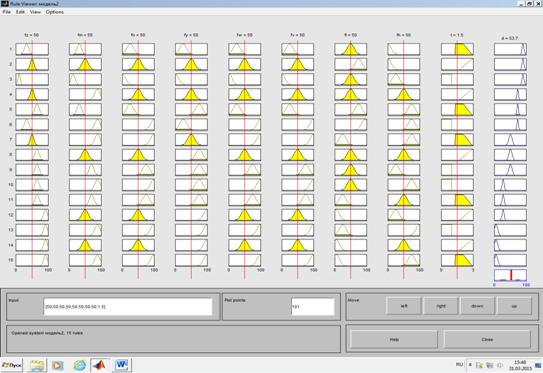
Рис.2. Результат дефазификации выходной переменой d
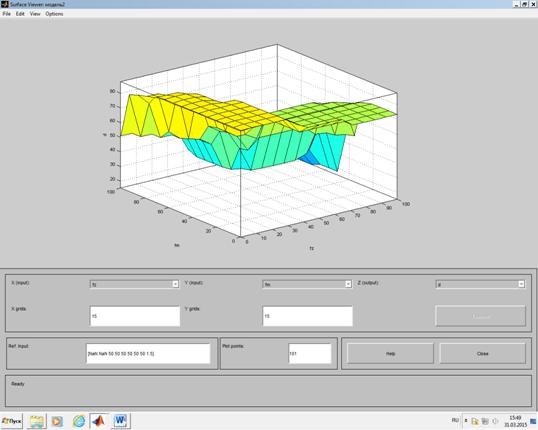
Рис. 3. Графическое представление результатов дефазификации выходной переменой d
Разработанная система является иерархической.
К сожалению, расширение Fuzzy Logic Toolbox, которое отвечает за нечеткое моделирование, не может одновременно проводить операции фазификации и дефазификации. Нечеткий вывод выполняется для промежуточных переменных с последующей передачей четких значений этих переменных в нечеткие системы следующего уровня иерархии. Поэтому над каждыми промежуточными значениями выполняются операции фазификации и дефазификации.
Разработанная модель прогнозирования уровня инновационного развития отрасли позволяет с достаточной достоверностью прогнозировать динамику при известных статистических и экспертных значениях входных параметров. Модель прогнозирования является универсальной и может быть адаптирована к различным отраслям. При накоплении базы знаний, т. е. зависимости выходных характеристик от входных переменных, модель будет работать в режиме реального времени, постоянно «самообучаться» и повышать достоверность сделанных прогнозов.
Выяснено, что модель прогнозирования имеет достаточно большую степень достоверности – уровень погрешности составляет чуть менее 3%.
На рисунке 4 представлено сравнение реального и прогнозного значений уровня инновационного развития отрасли.
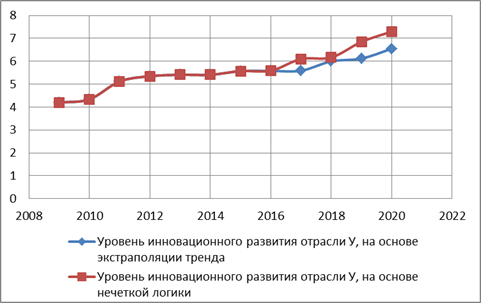
Рис. 4. Фактические и прогнозные значения показателя уровня инновационного развития отрасли, полученные на основе экстраполяции линии тренда и прогноза на основе нечеткой логики
Выводы
Введение разработанной модели оценки и прогнозирования уровня инновационного развития должно обеспечить адекватное управление инновационными процессами в данной стратегически важной отрасли экономики. Кроме того, указанная модель может рассматриваться как типичная для приведенного класса объектов, а разработанная на ее базе методология моделирования может применяться для других экономических систем, характеризующихся нечеткой связью между входными и выходными параметрами, трудностями формализации факторов влияния. Есть возможность привлечения экспертных знаний для построения модели.
Использование инструмента нечеткой логики при построении прогнозов развития отрасли должно стать составной частью общей методологии управления инновационным развитием.
Рецензенты:Корецкая Л.К., д.э.н., профессор, профессор кафедры «Экономика и финансы» Владимирского филиала Финуниверситета, г. Владимир;
Тесленко И.Б., д.э.н., зав. кафедрой «Бизнес-информатика и экономика», профессор, ВлГУ, г. Владимир.
Библиографическая ссылка
Губернаторов А.М., Никифорова С.В. МЕТОДОЛОГИЯ ИНФОРМАЦИОННОГО ОБЕСПЕЧЕНИЯ МЕХАНИЗМА ПРОГНОЗИРОВАНИЯ УРОВНЯ ИННОВАЦИОННОГО РАЗВИТИЯ ОТРАСЛЕВОГО КОМПЛЕКСА НА ОСНОВЕ КОНЦЕПЦИИ НЕЧЕТКОЙ ЛОГИКИ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=19048 (дата обращения: 12.03.2026).



