Дифракционные решетки нашли широкое применение в исследованиях спектрального состава излучения отдельных атомов /6/. Максимумы спектральных линий позволяют получать информацию о длине волны светового потока и его интенсивности. В настоящее время видеоинформация, получаемая с помощью дифракционных решеток, может быть преобразована в цифровую форму, и появляется возможность дополнительной обработки видеоизображений спектральных линий на ЭВМ. При обработке сигналов в радиотехнике используются положения теории оптимального приема /4,5/. Они позволяют решать такие статистические задачи, как обнаружение сигнала, оценка параметров сигнала, разрешение сигналов. Применение методов обработки теории оптимального приема в спектроскопии атомов химических элементов позволяет существенно повысить точность и достоверность оценки параметров спектральных линий, увеличить разрешение спектральных линий. Возможность применения положений теории оптимального приема для обработки спектральных линий отдельных атомов обосновывается линейностью преобразований светового потока в дифракционной решетке. Ряд исследований по вопросам обработки видеоизображений спектральных линий химических элементов методами теории оптимального приема изложен в работах /1,2,3,7/. В работе /1/ показана возможность повышения точности оценок амплитуды и длины волны светового потока за счет интегральной оценки. В работах /2,3/ показана возможность повышения разрешения двух близких спектральных линии при использовании метода максимального правдоподобия. Дисперсия амплитуд (дисперсия Рао-Крамера) дает возможность определить рабочую область, в которой могут быть разрешены близкие спектральные линии. Рабочая область определяется коэффициентом корреляции между спектральными линиями, который может меняться в пределах от нуля до значения 0,9. В настоящей работе продолжено исследование возможностей обработки видеоизображений спектральных линий отдельных атомов химических элементов методами теории оптимального приема. Основной задачей является обработка совокупности спектральных линий с автоматическим распознаванием структуры линий: одинарная линия (одна линия спектра) или двойная (две неразрешенные линии спектра). По существу, это задача фильтрации совокупности спектральных линий. При ее решении появляется возможность автоматизировать процесс съема данных.
Основы теории
Запишем принятое сообщение, содержащее сигнал в виде совокупности спектральных линий и аддитивный шум /4,5,6/:
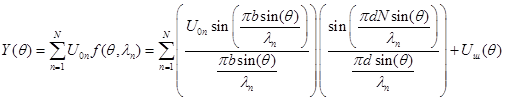 (1)
(1)
где ![]() — угол дифракции света;
— угол дифракции света;
![]() — параметры дифракционной решетки: ширина щели, период, количество щелей;
— параметры дифракционной решетки: ширина щели, период, количество щелей;
![]() — амплитуда
— амплитуда ![]() -спектральной линии, пропорциональная квадратному корню из соответствующей интенсивности света;
-спектральной линии, пропорциональная квадратному корню из соответствующей интенсивности света;
![]() — аддитивный нормальный шум со средним значением, равным нулю, дисперсией
— аддитивный нормальный шум со средним значением, равным нулю, дисперсией ![]() и интервалом корреляции
и интервалом корреляции ![]() .
.
В интервале изменений угла дифракции ![]() могут находиться как разрешенные по критерию Рэлея (одинарные) линии спектра, так и неразрешенные (двойные), характеризующиеся коэффициентом корреляции, отличным от нуля. Положение
могут находиться как разрешенные по критерию Рэлея (одинарные) линии спектра, так и неразрешенные (двойные), характеризующиеся коэффициентом корреляции, отличным от нуля. Положение ![]() -линии спектра определяется известным выражением (2):
-линии спектра определяется известным выражением (2):
![]() (2)
(2)
где ![]() — порядок спектральных линий.
— порядок спектральных линий.
Корреляционная обработка совокупности ортогональных спектральных линий, коэффициент корреляции между которыми равен нулю, позволяет получать интегральные оценки амплитуд ![]() и длин волн
и длин волн ![]() , повышая точность оценок. Для вывода основных соотношений корреляционной обработки запишем логарифм функции правдоподобия в виде:
, повышая точность оценок. Для вывода основных соотношений корреляционной обработки запишем логарифм функции правдоподобия в виде:
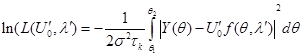 (3)
(3)
Штрихами отмечены оценочные значения амплитуды и длины волны света. Особенностью этого выражения является то, что принятому сообщению, содержащему ![]() спектральных линий, сопоставляется сигнал в виде одной линии спектра. При дифференцировании логарифма функции правдоподобия по амплитуде
спектральных линий, сопоставляется сигнал в виде одной линии спектра. При дифференцировании логарифма функции правдоподобия по амплитуде ![]() и приравнивании дифференциала к нулю можно получить выражение:
и приравнивании дифференциала к нулю можно получить выражение:
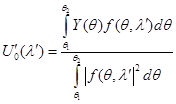 (4)
(4)
Выражение (4) будет более понятно, если выполнить операцию математическое ожидание от ![]() :
:
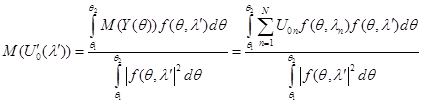 (5)
(5)
В условиях ортогональности спектральных линий выражение (5) определяет ![]() максимумов при
максимумов при ![]() (
(![]() ). В результате реализуется процесс корреляционной обработки принятой реализации с рэлеевским ограничением на разрешение спектральных линий. По своей структуре выражение (4) определяет процесс фильтрации принятой реализации фильтром с импульсной характеристикой вида:
). В результате реализуется процесс корреляционной обработки принятой реализации с рэлеевским ограничением на разрешение спектральных линий. По своей структуре выражение (4) определяет процесс фильтрации принятой реализации фильтром с импульсной характеристикой вида:
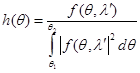 (6)
(6)
Для получения высокого разрешения спектральных линий вместе с корреляционной обработкой используется метод максимального правдоподобия. Его основой является логарифм функции правдоподобия, записанный в виде:
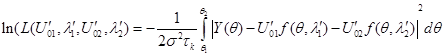 (7)
(7)
В этом выражении принятому сообщению, содержащему ![]() линий спектра, сопоставляется сигнал, состоящий из двух близких спектральных линий. Дифференцируя (7) по параметрам
линий спектра, сопоставляется сигнал, состоящий из двух близких спектральных линий. Дифференцируя (7) по параметрам ![]() и приравнивая дифференциалы к нулю, можно получить систему уравнений правдоподобия:
и приравнивая дифференциалы к нулю, можно получить систему уравнений правдоподобия:
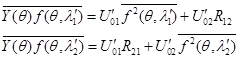 (8)
(8)
Черта сверху означает интегрирование по параметру ![]() .
.
![]() — ненормированный коэффициент корреляции между двумя спектральными линиями.
— ненормированный коэффициент корреляции между двумя спектральными линиями.
Решая систему (8) относительно амплитуд ![]() , можно получить:
, можно получить:
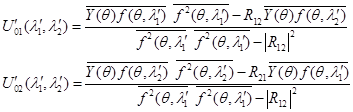 (9)
(9)
Полученные оценочные значения амплитуд ![]() зависят от оценочных значений длин волн
зависят от оценочных значений длин волн ![]() и, в принципе, не могут решить задачу разрешения двух линий спектра. Для получения решения необходимо подставить полученные оценки амплитуд в функционал правдоподобия
и, в принципе, не могут решить задачу разрешения двух линий спектра. Для получения решения необходимо подставить полученные оценки амплитуд в функционал правдоподобия ![]() .
.
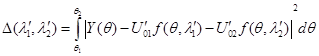 (10)
(10)
В этом случае исключаются неизвестные амплитуды, и функционал будет зависеть лишь от ![]() . Преобразуем выражение (10) с учетом (8).
. Преобразуем выражение (10) с учетом (8).
![]() (11)
(11)
Черта сверху означает интегрирование по параметру ![]() .
.
Данный функционал представляет собой поверхность в двумерном пространстве ![]() . В точке поверхности функционала
. В точке поверхности функционала ![]() реализуется минимум, который является критерием отбора решений при переборе параметров
реализуется минимум, который является критерием отбора решений при переборе параметров ![]() в области их определения. Таким образом, создавая поверхность функционала и определяя минимум этой поверхности, можно получить решение задачи разрешения двух спектральных линий:
в области их определения. Таким образом, создавая поверхность функционала и определяя минимум этой поверхности, можно получить решение задачи разрешения двух спектральных линий: ![]() .
.
Результаты модельных исследований
При проведении модельных расчетов принято следующее. Ширина щели дифракционной решетки ![]() м, период решетки
м, период решетки ![]() м, количество щелей
м, количество щелей ![]() , интервал между отсчетами
, интервал между отсчетами ![]() градусов, длины волн двух потоков света
градусов, длины волн двух потоков света ![]() м,
м, ![]() м, интервал обработки
м, интервал обработки ![]() ÷
÷ ![]() . Согласно критерию Рэлея для разрешения двух спектральных линий необходимо выполнение неравенства:
. Согласно критерию Рэлея для разрешения двух спектральных линий необходимо выполнение неравенства: ![]() м. Различие между длинами волн при модельных расчетах
м. Различие между длинами волн при модельных расчетах ![]() м. Следовательно, данные две линии спектра являются неортогональными и корреляционный анализ не может их разрешить.
м. Следовательно, данные две линии спектра являются неортогональными и корреляционный анализ не может их разрешить.
На рисунке 1 показан результат расчета линий спектра методом корреляционного анализа и методом максимального правдоподобия. Принятое сообщение содержит две близкие спектральные линии, коэффициент корреляции между которыми равен ![]() . Метод корреляционного анализа не может разрешить эти две линии спектра. Метод максимального правдоподобия полностью решает задачу разрешения этих двух линий спектра.
. Метод корреляционного анализа не может разрешить эти две линии спектра. Метод максимального правдоподобия полностью решает задачу разрешения этих двух линий спектра.
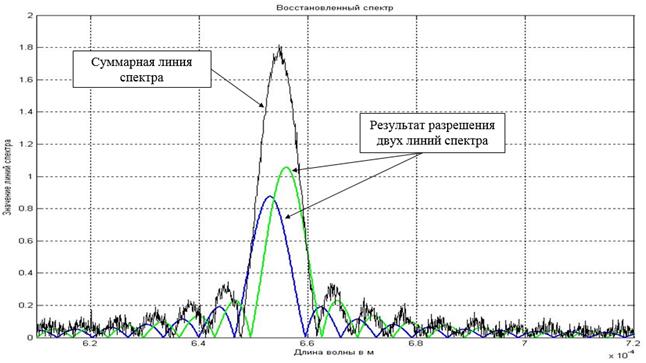
Рис. 1. Суммарная линия спектра содержит две спектральные линии с длинами волн ![]() м и
м и ![]() м. и амплитудами
м. и амплитудами ![]()
При этом получены следующие оценки параметров: ![]() .
.
Если в принятом сообщении содержится лишь одна линия спектра, тогда результаты расчета методом максимального правдоподобия и методом корреляционного анализа одинаковы. Вторая линия спектра в методе максимального правдоподобия определяется по одному из шумовых максимумов. В результате амплитуда этой ложной спектральной линии будет на уровне шума и легко устраняется. Динамический диапазон разрешения двух линий спектра методом максимального правдоподобия ограничен уровнем шума. На рисунке 2 показан этот случай.
Если в принятом сообщении не содержится спектральных линий, тогда метод корреляционного анализа и метод максимального правдоподобия дают решения с амплитудами на уровне шума.
Процесс фильтрации совокупности спектральных линий двумя методами (методом корреляционного анализа и методом максимального правдоподобия) представлен на следующих рисунках.
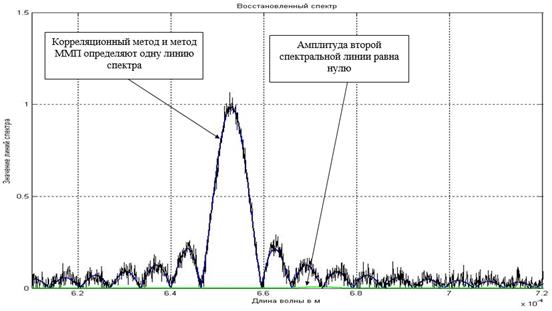
Рис. 2. Принятое сообщение содержит одну линию спектра с длиной волны ![]() м. Метод максимального правдоподобия (ММП) и корреляционный метод определяют одну линию спектра с оценкой
м. Метод максимального правдоподобия (ММП) и корреляционный метод определяют одну линию спектра с оценкой ![]() м.
м.
Амплитуда второй спектральной линии равна нулю
Принятое сообщение содержит четыре спектральные линии со следующими длинами волн: ![]() м,
м, ![]() м.,
м., ![]() м,
м, ![]() м. Они соответствуют синей, зеленой и двум близким желтым линиям атома ртути. Амплитуда света равна единице, угол падения равен нулю. На рисунке 3 показаны спектральные линии атома ртути второго порядка.
м. Они соответствуют синей, зеленой и двум близким желтым линиям атома ртути. Амплитуда света равна единице, угол падения равен нулю. На рисунке 3 показаны спектральные линии атома ртути второго порядка.
Две желтые линии спектра неразрешимы по критерию Рэлея. Коэффициент корреляции между этими линиями равен ![]() . На рисунке 4 показан результат скользящей корреляционной обработки спектральных линий атомов ртути второго порядка. Интервал обработки равен ширине спектральных максимумов. Согласно данному рисунку две желтые линии спектра не могут быть разрешены методом корреляционной обработки.
. На рисунке 4 показан результат скользящей корреляционной обработки спектральных линий атомов ртути второго порядка. Интервал обработки равен ширине спектральных максимумов. Согласно данному рисунку две желтые линии спектра не могут быть разрешены методом корреляционной обработки.
При корреляционной обработке шумовая составляющая уменьшилась, но двойная желтая линия так и осталась неразрешенной.
На рисунке 5 показан результат скользящей обработки совокупности линий спектра методом максимального правдоподобия. Согласно данному рисунку две желтые линии спектра оказались разрешенными. Синяя и зеленая линии спектра по критерию амплитуды определены как одинарные линии спектра.
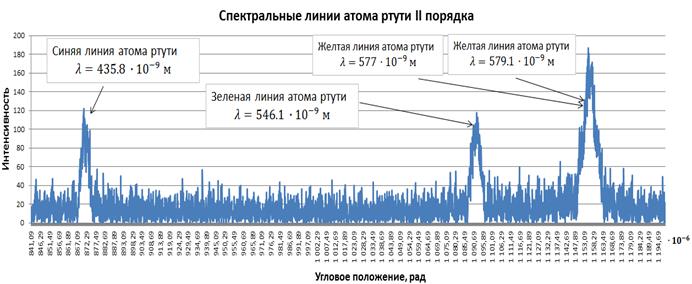
Рис. 3. Спектральные линии атома ртути II порядка
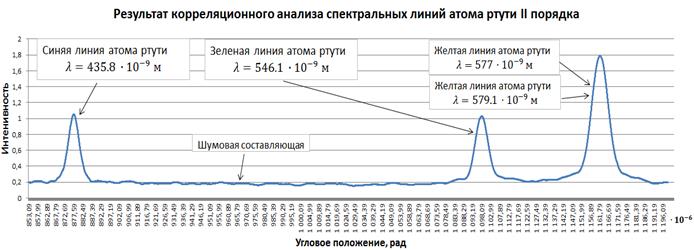
Рис. 4. Результат корреляционного анализа спектральных линий атома ртути II порядка
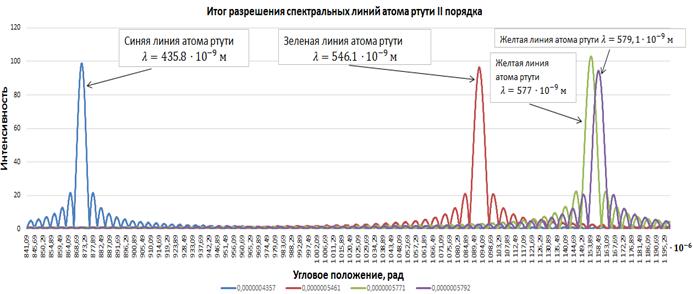
Рис. 5. Фильтрация спектральных линий методом максимального правдоподобия
Заключение
В настоящей работе рассмотрена возможность процесса фильтрации спектральных линий атомов химических элементов методом максимального правдоподобия. Выведены основные выражения, определяющие алгоритмы скользящей обработки методом корреляционного анализа и методом максимального правдоподобия. Представлены результаты модельных расчетов. По результатам работы можно сделать вывод: метод максимального правдоподобия позволяет проводить скользящую фильтрацию совокупности спектральных линий с автоматическим различением одинарных и двойных линий спектра. Метод может быть использован для автоматизации процесса съема данных, получаемых с помощью дифракционной решетки.
Рецензенты:
Захаров В.Е., д.ф.-м.н., профессор, заведующий кафедрой радиофизики и информационной безопасности Балтийского федерального университета им. И. Канта Минобрнауки, г. Калининград;
Никитин М.А., д.ф.-м.н., профессор кафедры физики БФУ им. И. Канта, г. Калининград.
Библиографическая ссылка
Бабинович А.И., Пахотин В.А., Бессонов В.А. ФИЛЬТРАЦИЯ СПЕКТРАЛЬНЫХ ЛИНИЙ МЕТОДОМ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=19012 (дата обращения: 12.03.2026).



