Одними из наиболее важных технологических свойств композиционных материалов, которые оказывают значительное влияние на качество формирующейся структуры, являются подвижность и удобоукладываемость смеси. Реологические свойства композитов на основе серного вяжущего зависят от ряда рецептурно-технологических факторов, а именно: вида и дисперсности наполнителя, степени наполнения материала, вида и количества модифицирующей добавки, а также от интенсивности физико-химического взаимодействия на границе раздела фаз «сера - наполнитель», температуры компонентов при совмещении, способа и условий приготовления материала [4].
В большинстве случаев, для описания поведения строительных материалов в период нахождения их в пластичновязком состоянии используют реологические характеристики: коэффициент структурной вязкости и предельное напряжение сдвига [1, 5…7]. В настоящей работе реологические свойства исследуемых серных мастик оценивали величиной предельного напряжения сдвига.
Предельное напряжение сдвига серных мастик определяли с помощью цилиндрического вискозиметра по величине гравитационного расплыва при температуре 150...160°С [3]. Предельное напряжение сдвига рассчитывали по формуле:
![]() , (1)
, (1)
где t - предельное напряжение сдвига, Па; h и d - высота и диаметр вискозиметра, м; ![]() - плотность серной мастики, кг/м3; g - ускорение свободного падения; D - диаметр расплыва серной мастики, м; k - коэффициент, учитывающий перераспределение напряжений в вязкопластических телах, равный 2.
- плотность серной мастики, кг/м3; g - ускорение свободного падения; D - диаметр расплыва серной мастики, м; k - коэффициент, учитывающий перераспределение напряжений в вязкопластических телах, равный 2.
Результаты исследований представлены на рис. 1.

Рис. 1. Зависимость предельного напряжения сдвига серных мастик от степени наполнения и удельной поверхности наполнителя
Математическая обработка экспериментальных данных, представленных на рис. 1, показывает, что зависимость предельного напряжения сдвига серных мастик от степени наполнения описывается функцией вида:
![]() , (2)
, (2)
где ![]() – предельное напряжение сдвига; nf – объёмная доля наполнителя; а, b – эмпирические коэффициенты, значения которых приведены в табл. 1.
– предельное напряжение сдвига; nf – объёмная доля наполнителя; а, b – эмпирические коэффициенты, значения которых приведены в табл. 1.
Анализ уравнения (1) показывает, что коэффициент а равен предельному напряжению сдвига ненаполненного серного вяжущего, а коэффициент b характеризует влияние наполнителя на подвижность мастики.
Таблица 1
Значения эмпирических коэффициентов
|
Удельная поверхность, м2/кг |
Эмпирические коэффициенты |
|
|
a |
b |
|
|
180 |
2,67 |
7,92 |
|
300 |
3,43 |
8,08 |
|
420 |
4,67 |
8,83 |
Анализ данных, представленных на рис. 1 показывает, что с увеличением удельной поверхности наполнителя наблюдается закономерное снижение подвижности серных мастик. Из рис. 1 также видно, что на зависимостях «предельное напряжение сдвига - объёмная степень наполнения» можно выделить две параметрические точки. Эти точки соответствуют некоторым предельным концентрациям наполнителя, при которых происходят изменения структуры серной мастики. При малых концентрациях наполнителя серная мастика является механической смесью, в которой влияние поверхностных явлений невелико. Реологические свойства таких смесей описываются уравнением А. Эйнштейна:
![]() , (3)
, (3)
где ![]() – коэффициент, учитывающий форму частиц наполнителя;
– коэффициент, учитывающий форму частиц наполнителя; ![]() – объёмная степень наполнения; tо – предельное напряжение сдвига серного вяжущего.
– объёмная степень наполнения; tо – предельное напряжение сдвига серного вяжущего.
Объёмная доля наполнителя, при которой наблюдается отклонение от теоретических значений ![]() , рассчитанных по уравнению Эйнштейна, является координатой первой параметрической точки
, рассчитанных по уравнению Эйнштейна, является координатой первой параметрической точки ![]() . Дальнейшее увеличение содержания наполнителя приводит к сближению частиц и интенсификации их взаимодействия между собой. При достижении определённой степени наполнения (вторая параметрическая точка
. Дальнейшее увеличение содержания наполнителя приводит к сближению частиц и интенсификации их взаимодействия между собой. При достижении определённой степени наполнения (вторая параметрическая точка ![]() ) наблюдается резкое повышение структурной прочности серной мастики, что можно объяснить образованием структуры с более однородным распределением фаз, на разрушение которой требуется подвести большее количество энергии.
) наблюдается резкое повышение структурной прочности серной мастики, что можно объяснить образованием структуры с более однородным распределением фаз, на разрушение которой требуется подвести большее количество энергии.
Значения параметрических точек серных мастик, изготовленных на кварцевой муке, приведены в табл. 2.
Таблица 2
Значения параметрических точек
|
Удельная поверхность, м2/кг |
Параметрические точки |
|
|
|
|
|
|
180 |
0,12 |
0,35 |
|
300 |
0,12 |
0,34 |
|
420 |
0,12 |
0,33 |
Как видно из табл. 2, увеличение удельной поверхности наполнителя приводит к закономерному смещению координат параметрических точек в область меньших степеней наполнения.
Зависимости предельного напряжения сдвига серных мастик от соотношения h/df приведены на рис. 2.
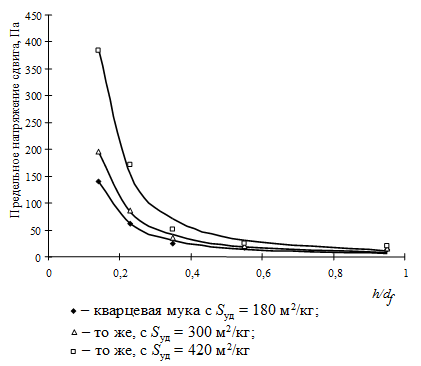
Рис. 2. Зависимость предельного напряжения сдвига серных мастик от соотношения h/df
Математическая обработка экспериментальных данных рис. 2 показывает, что аппроксимирующая функция имеет вид:
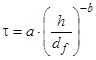 , (4)
, (4)
где а, b - эмпирические коэффициенты, значения которых приведены в табл. 3.
Таблица 3
Значения эмпирических коэффициентов
|
Удельная поверхность, м2/кг |
Эмпирические коэффициенты |
|
|
a |
b |
|
|
180 |
5,23 |
1,67 |
|
300 |
6,84 |
1,71 |
|
420 |
10,02 |
1,86 |
Для серных композитов на аппретированном каучуком наполнителе важным фактором также является продолжительность изотермической выдержки tT, определяющая количество образующейся полимерной серы, степень превращения аппрета и свойства образующегося вулканизата (рис. 3).
Анализ экспериментальных данных (рис. 3) показывает, что с увеличением продолжительности изотермической выдержки серных композитов, наполненных кварцевой мукой без аппрета, наблюдается незначительное снижение подвижности смеси. Это очевидно связано с образованием некоторого количества полимерной серы. Зависимость предельного напряжения сдвига серной мастики на неаппретированной кварцевой муке от продолжительности изотермической выдержки описывается функцией вида:
![]() , (5)
, (5)
где ![]() – предельное напряжение сдвига, Па;
– предельное напряжение сдвига, Па; ![]() – продолжительность изотермической выдержки; а, b – эмпирические коэффициенты, значения которых приведены в табл. 4.
– продолжительность изотермической выдержки; а, b – эмпирические коэффициенты, значения которых приведены в табл. 4.
Введение в расплав серы наполнителя, обработанного аппретом, приводит к увеличению предельного напряжения сдвига серных мастик (рис. 3). Это можно объяснить протеканием двух конкурирующих процессов, связанных с вулканизацией каучука.
Очевидно, что образование полимерной серы и вулканизата приводит к снижению подвижности смеси с увеличением времени реакции:
![]() . (6)
. (6)
Одновременно с процессами образования полимерной серы и вулканизата происходит выделение газообразных продуктов вулканизации, которые способствуют снижению величины предельного напряжения сдвига:
![]() . (7)
. (7)
а)
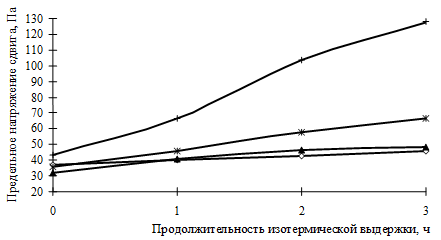
б)
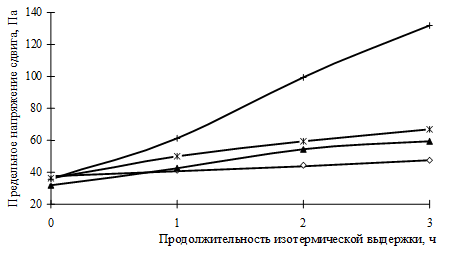
в)
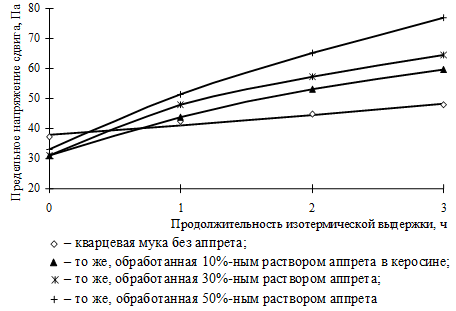
Рис. 3. Зависимость предельного напряжения сдвига серных мастик на кварцевой муке от продолжительности изотермической выдержки и концентрации аппрета: а) кварцевая мука с Sуд = 180 м2/кг, nf = 0,4; б) то же с Sуд = 300 м2/кг, nf = 0,35; в) то же с Sуд = 420 м2/кг, nf = 0,3
С учётом влияния газовой фазы совместное влияние указанных процессов на предельное напряжение сдвига описывается функцией вида (в соответствии с законом Гута-Марка газовая фаза снижает вязкость системы [2]):
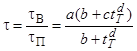 , (8)
, (8)
где а, b, c, d – эмпирические коэффициенты, значения которых приведены в табл. 4.
Таблица 4
Значения эмпирических коэффициентов уравнений (7) и (8)
|
Концентрация аппрета, % от массы серы |
Эмпирические коэффициенты |
|||
|
a |
b |
c |
d |
|
|
Sуд=180 м2/кг (nf =0,4) |
||||
|
0 |
37,23 |
0,07 |
– |
– |
|
0,2 |
31,97 |
1,01 |
1,53 |
2,49 |
|
0,6 |
35,84 |
3,99 |
2,42 |
1,62 |
|
1,0 |
43,11 |
4,28 |
3,84 |
2,06 |
|
Sуд=300 м2/кг (nf =0,35) |
||||
|
0 |
37,53 |
0,08 |
– |
– |
|
0,2 |
32,00 |
2,01 |
1,97 |
2,43 |
|
0,6 |
36,23 |
6,87 |
4,04 |
0,89 |
|
1,0 |
35,65 |
7,08 |
6,86 |
1,64 |
|
Sуд=420 м2/кг (nf =0,3) |
||||
|
0 |
37,99 |
0,08 |
– |
– |
|
0,2 |
31,16 |
4,03 |
3,04 |
1,08 |
|
0,6 |
31,00 |
14,32 |
9,41 |
0,68 |
|
1,0 |
32,98 |
34,58 |
20,99 |
0,82 |
Таким образом, анализ результатов проведенных исследований показывает, что на реологические свойства серных мастик значительное влияние оказывают процессы, протекающие на границе раздела фаз «сера - наполнитель», интенсивность которых можно регулировать количеством и дисперсностью наполнителя, концентрацией аппрета, а также продолжительностью изотермической выдержки.
Рецензенты:
Логанина В.И., д.т.н., профессор, заведующая кафедрой управления качеством и технологий строительного производства Пензенского Государственного университета архитектуры и строительства, г. Пенза;
Калашников В.И., д.т.н., профессор, заведующий кафедрой технологии строительных материалов и деревообработки Пензенского Государственного университета архитектуры и строительства, г. Пенза.
Библиографическая ссылка
Шитова И.Ю., Самошина Е.Н., Базин В.В., Жуков А.в. ПРЕДЕЛЬНОЕ НАПРЯЖЕНИЕ СДВИГА СЕРНЫХ МАСТИК НА КВАРЦЕВОМ НАПОЛНИТЕЛЕ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18952 (дата обращения: 12.03.2026).



