Результаты ряда научных исследований [3, 4, 9] свидетельствуют о том, что сложившиеся в предшествующие годы тенденции ухудшения здоровья студентов принимают устойчивый характер. Наблюдаются неблагоприятная динамика основных показателей здоровья молодежи, учащение перехода острых форм заболеваний в хронические и т.д. Объясняется это не только экономической ситуацией, социальным напряжением и ухудшением экологической обстановки в России. Важнейшим фактором является отношение к здоровью как к индивидуальной и социальной ценности. К сожалению, далеко не все студенты соблюдают нормы и правила здорового образа жизни [7]. Особенностью современных молодых людей является повышение распространенности среди них аутоагрессивных видов поведения, таких как курение, употребление алкоголя, наркотиков, связанное с риском половое поведение, что существенно усугубляет негативные тенденции состояния здоровья, наблюдаемые в настоящий период.
Очевидно, что здоровье молодежи является важнейшей проблемой государства, так как составляет основу кадрового, экономического потенциала страны, определяет ее обороноспособность. Репродуктивное здоровье молодежи имеет решающее значение для воспроизводства населения и здоровья будущих поколений.
Следует отметить, что высшие учебные заведения могут организовать эффективную оздоровительную и реабилитационную работу среди студенческой молодежи. Одним из результативных вариантов решения рассматриваемой проблемы является внедрение в деятельность образовательных организаций современных комплексных медико-педагогических технологий, что является целью нашего исследования [2].
Учитывая актуальность вышеизложенного, мы проводим комплексную оценку состояния здоровья студентов 1–4-х курсов высших учебных заведений г. Уфа (БГУ, БГПУ, УГАТУ и др.). В рамках нашего исследования проводится изучение заболеваемости студентов по данным обращаемости, с временной утратой трудоспособности в случаях и днях госпитализированной заболеваемости [4]. Особое внимание было уделено анализу репродуктивного здоровья студенток. Производилась также оценка некоторых показателей психического здоровья студентов посредством тестирований.
Рассматриваемая в статье медико-социальная система характеризуется высоким уровнем априодной неопределенности.
Известны три группы методов, способных эффективно работать в отмеченных сложных условиях при сильных зашумленных данных:
1) нейросетевые методы (HCM) [11];
2) методы нечеткого описания модели и правил логического вывода [6];
3) нейро-нечеткие методы [13].
В данной статье использовали адаптивные нейросетевые методы. Однако, несмотря на их эффективность в условиях сильного зашумления данных, здесь возникли две проблемы:
-
неустойчивость модели к вариации входных данных при выходе за пределы некоторого критического уровня шума при оценке анкетных данных студентов и результатов психологических тестирований;
-
оценка и обеспечение адекватности нейросетевой модели в условиях нарушения практически всех предпосылок классического регрессионного анализа [1].
Для решения этих проблем в статье разработан байесовский подход (концепция) нейросетевого моделирования, подробно изложенная ниже.
1. Постановка задачи моделирования
Пусть в качестве инструмента моделирования при обработке анкетных данных используется нейросетевой эмулятор (программной продукт, например Neuro Solutions 5.0), реализующий нейросеть типа многослойного персептрона (Multi Lauer Perseptron (MLP)) с алгоритмом обучения типа обратного распространения ошибки (Back Propagation Error (BP)). MLP-BP-нейросеть является универсальным аппроксиматором [11]:
); m=
,
где 
т-я моделируемая (эндогенная) расчетная величина, т.е. показатель обследования, характеризующий определенный уровень здоровья;
…, 
…, 
) – вектор экзогенных (объясняющих) переменных (далее коротко «факторов»), которые могут быть как количественными, так и качественными; W — матрица синаптических весов, т.е. весовых коэффициентов сигналов 
, поступающих от р-го нейрона к следующему за ним нейрону сети в направлении прямого распространения сигналов от входа к выходу; F(
) — оператор нейросетевого отображения сигналов, представляющий собой композицию двух операторов F: 
, который в каждым нейроне (элементарном процессоре) нейросети реализует две последовательные операции:
1.
() – весового суммирования сигналов поступающих сети на вход р-го нейрона в промежуточном (скрытом) слое; 
=
;
2. () – нелинейного преобразования результата суммирования, например с помощью функции гиперболического тангенса 
()=
)=th ().
Функцию 
) называют активационной, или передаточной. Обычно в выходном слое нейросети используется линейная функция.
Замечание 1. Задача аппроксимации данных в математическом аспекте является обратной задачей, т.е. требуется найти причины явления по заданному следствию – наблюдаемым характеристикам системы. Решение таких задач гораздо сложнее, чем прямых задач прямого расчета. С содержательной точки зрения задачи аппроксимации данных суть задачи восстановления многомерных нелинейных закономерностей, скрытых в данных. Физики их называют также задачами интерпретации. Как известно [11], задачи этого класса являются некорректно поставленными по Адамару и поэтому нуждаются в специальных мерах регуляризации.
Замечание 2. Принципиальным отличием нейросетевых методов от классических методов регрессионного анализа [6], где вектор факторов 
считается детерминированным, а выходные величины 
— случайными величинами, является то, что в НСМ вектор тоже считается случайным. Этот подход к построению модели значительно увеличивает прогностическую силу НСМ, приближая его к реальным условиям моделирования, однако исключает применимость традиционных методов оценки адекватности модели.
Замечание 3. В НСМ относительно просто решается вопрос учета многомерности вектора выходных величин 
=
Нужно лишь в выходном слое сети взять не один, а несколько нейронов по числу компонент вектора .
Можно также выходной слой реализовать в виде агрегатора (свертки), т.е. НСМ будет давать на выходе некоторый обобщенный критерий Ф
уровня здоровья обучающейся молодежи.
2. Идея разработки концепции регуляризации нейросетевой модели
Идея 1 предлагаемой концепции байесовского подхода к регуляризации НСМ вполне понятна на интуитивном уровне. Восстанавливаемая функциональная зависимость Y
аппроксимируется не одной моделью, а ансамблем адаптивных параметрических моделей с априорным выбором их вида, причем все выходные характеристики моделирования получаются путем осреднения (прямого или весового) на отфильтрованном по критерию качества НСМ ансамбле. При этом «эксплуатируется» широко известная закономерность теории вероятностей: среднее значение случайной величины 
колеблется в наблюдениях гораздо меньше, чем сама случайная величина Y, причем тем меньше, чем больше число наблюдений N.
Идея 2, основная для разработки предлагаемой концепции, состоит в том, что регуляризация НСМ на байесовском ансамбле априорно выбираемых нейросетевых моделей-гипотез 
, q=
, 
где H – общий для всех гипотез класс моделей (мета-гипотеза) и затем фильтруемых по качеству, укладывается в общую парадигму теории регуляризации обратных задач А.Н. Тихонова [8]. Суть этой парадигмы состоит в том, что регуляризация и соответственно повышение устойчивости модели достигается «сужением класса искомых решений обратной задачи» с использованием априорной информации о решении.
Пути реализации этой парадигмы при разработке концепций могут быть разными: в теории А.Н. Тихонова [8] априорная информация используется при конструировании специальных стабилизаторов Тихонова, а в нашей концепции — при задании архитектуры нейросетей 
в байесовском ансамбле и выборе активационных функций.
3.Алгоритм метода регуляризации НСМ
В известных работах по байесовской регуляризации нейросетевых моделей [10], как правило, задача решается аналитически на основе вычисления функции правдоподобия. Это сопряжено с введением допущения об априорном задании закона распределения плотности вероятности шумов в данных, которое на практике часто не выполняется.
Мы отказались от этого весьма жесткого допущения, заменив его вычислением вероятностного частотного критерия апостериорной фильтрации НСМ ансамбля по качеству аппроксимации данных. Детализируем алгоритм предлагаемого квазибайесовского метода регуляризации (КБМР).
1. Опишем алгоритм метода по шагам, т.е. будем полагать, что отсутствуют какие-либо предпочтения между несколькими методами моделирования данных (мета-моделями) (P(H) = const), и мы можем выбрать мета-гипотезы на основе экспертных оценок и предварительных вычислительных экспериментов.
2. Построим байесовский ансамбль НСМ, который показан на рисунке 1, где введены обозначения: D – база данных; M – блоки масштабирования (нормировки); Cр – блок усреднения расчетных характеристик на отфильтрованном байесовском ансамбле; ДМ – блоки демасштабирования; S, C – множества выходных характеристик моделируемой системы; R2 – индекс множественной детерминации; RBF, MLP – типы нейросетей, входящих в байесовский ансамбль.
3. Принадлежность всех {hq} одному классу Н есть ограничение на нейросетевые модели – гипотезы, что и является механизмом регуляризации согласно основной парадигме регуляризации, используемой в монографии.
4. После обучения нейросетевых моделей-гипотез {hq} на экспериментальных примерах 
должна быть разработана числовая мера оценки апостериорной вероятности гипотез P(hq|D|H) о порождении данных. Эта мера служит критерием отбора для процедуры (фильтрации) гипотез-нейросетей {hq}, сужающим априорный ансамбль. В редуцированном ансамбле отсеиваются нейросети-гипотезы, у которых качество сети оказывается неудовлетворительным по выбранной числовой мере.
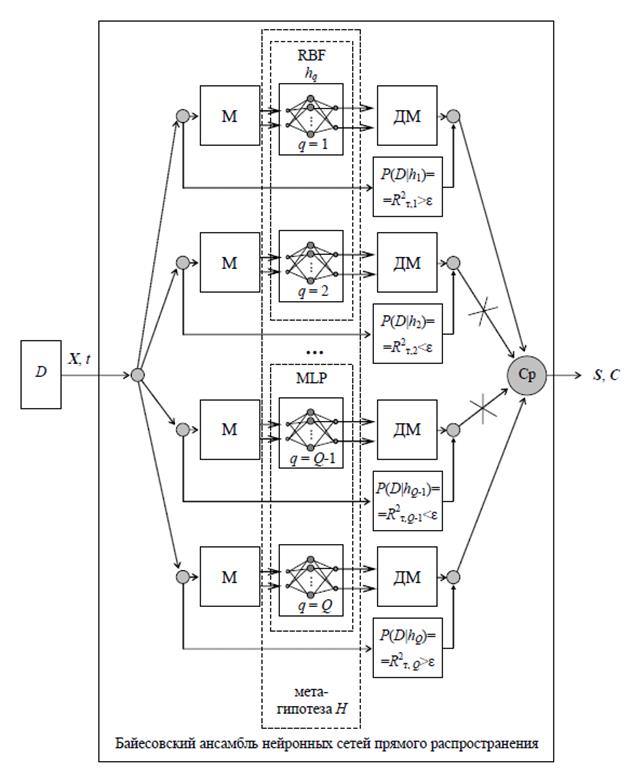
Рис. 1. Структура байесовского ансамбля нейросетевых моделей
Мы опирались на интуитивно понятное замечание, высказанное в [10]: «если функцию ошибок E(·) задать в виде числовой меры по модулю, то из максимизации P(D|hq,w) будет вытекать минимизация функции ошибок»
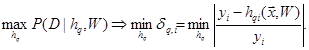(6)
Будем также учитывать, что в самом общем случае оценка максимального правдоподобия согласно [9] основывается на том, что «разные генеральные совокупности (population) генерируют различные данные, при этом происхождение любого заданного примера более правдоподобно для некоторой определенной совокупности, чем для остальных совокупностей».
Если под генеральными совокупностями понимать совокупности данных, порождаемых в соответствии с конкретной гипотезой-нейросетью 
, то для оценки апостериорных вероятностей гипотез – нейросетевых моделей о порождении данных 
можно предложить числовую меру:
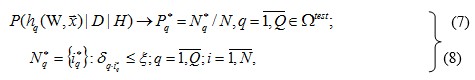
где: 
– число «хороших» точек, в которых остатки {δq,i}имеют приемлемый уровень ξ для q-ой гипотезы – нейросети 
; N – общее число примеров данных, одинаковое для всех гипотез-нейросетей; 
– тестовое множество примеров; стрелка «→» означает «оценку»; 
– номер «хорошей» точки; ξ – экспертно задаваемый параметр, например ξ=0,05…0,1.
Поскольку в предложенном методе не используется прямое вычисление функции правдоподобия P(D|h,H) в формуле Байеса, мы назвали его квазибайесовским методом регуляризации (КБМР).
По мнению авторов, в пользу предложенного критерия (7) – (8) говорят следующие соображения:
1) он очень прост в реализации и не требует никаких ограничивающих предположений о законах распределения шумов;
2) критерий является финишным и носит характер интегральной оценки качества объяснения сетью 
данных: он «вбирает» в себя оценки всех процедур предобработки данных, а также алгоритмов выбора мета-гипотезы Н, гипотез-нейросетей {hq} и качества их обучения;
3) в критерии (7)–(8) назначаемый уровень ξ играет роль параметра регуляризации, который согласует между собой два противоречивых требования – минимизацию критерия ошибок аппроксимации (6) и устойчивость НСМ, получаемые осреднением на байесовском ансамбле гипотез-нейросетей {hq}.
При таком подходе можно оптимизировать этот параметр с учетом показателя устойчивости S. Оптимальное значение параметра ξ* находится в результате оптимального итерационного процесса фильтрации байесовского ансамбля:
ξ≤ξ0, ξ0>0, (9)
где: черточка над 
означает усреднение по отфильтрованному ансамблю;
ξ0 – заданное число (предельно допустимый уровень ошибок).
Фильтрация априорных гипотез
Теперь мы можем сузить пространство априорных гипотез 
, т.е. провести их фильтрацию, отбраковав гипотезы с малой апостериорной вероятностью порождения данных D. Вычислим 
по (7)–(8) и оставим в ансамбле только те гипотезы, которые имеют достаточную апостериорную вероятность:
, (10)
где ω – экспертно задаваемый уровень апостериорной вероятности объяснения данных в байесовском ансамбле гипотез; x* – параметр регуляризации по (9).
Здесь ω – второй параметр регуляризации.
Замечание. Для оптимизации пары параметров (ξ, ω) можно применить схему алгоритма ЕМ из [10]:; а именно: поочередно на каждом шаге итераций k фиксируется ω(k-1) и оптимизируется ξ (k) по критерию (9), затем на следующем шаге (k+1) фиксируется ξ(k) и оптимизируется ω:
ω≥ω0, ω0>0. (11)
где: ω0 – предельно допустимый уровень снижения качества объяснения данных, определяемый контекстом задачи.
Результаты моделирования получаются путем усреднения на отфильтрованном ансамбле гипотез:
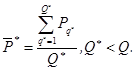(12)
где: 
– средняя по отфильтрованному байесовскому ансамблю гипотез-нейросетей апостериорная вероятность порождения наблюдаемых данных; значком «*» отмечены величины, относящиеся к отфильтрованному ансамблю; 
– апостериорная вероятность порождения данных D в соответствии с гипотезой 
при оптимальном значении параметра регуляризации ξ* согласно (9).
Замечание. От известного байесовского метода обучения нейросети [10] предложенный квазибайесовский метод регуляризации отличается следующими признаками.
I. Снято ограничение на необходимость аналитического задания какого-либо закона распределения шумов в данных.
II. Введена приближенная операция оценки апостериорных вероятностей 
III. Введена оптимизационная процедура для оценки параметров регуляризации ξ и ω.
IV. Введен алгоритм (9) апостериорной фильтрации байесовских гипотез – нейросетей 
в ансамбле.
V. 
Отметим также, что контролируемая длина описания нейросетевым байесовским ансамблем данных задается при его формировании в виде априорных гипотез 
, причем структурная оптимизация модели и выбор активационных функций 
в промежуточных слоях сети реализуются через механизм апостериорной фильтрации нейросетей 
по (10).
Направление дальнейших исследований
1. На реальных данных опросных анкет и тестов, направленных на изучение условий и образа жизни обучающейся молодежи, исследовать вопросы оценки адекватности нейросетевой модели, границ уровня зашумленности данных, в рамках которых эффективна предложенная концепция.
2. Использовать нейросетевую модель для комплексной оценки состояния здоровья студентов высших учебных заведений (изучить заболеваемость, показатели антропометрии, функциональных проб и пр.).
5. Выводы
-
На основе парадигмы регуляризации алгоритмов решения обратных задач восстановления многомерных нелинейных зависимостей, скрытых в данных, заключающейся в сужения класса искомых решений с использованием априорной информации об этих решениях, разработана концепция регуляризации нейросетевой модели.
-
Концепция разработана в деталях и реализована в квазибайесовском методе.
-
Предложенный квазибайесовский метод ослабляет остроту проблемы обеспечения адекватности НСМ, т.е. сводит ее к последовательному повышению достоверности и точности результатов моделирования на этапах априорного задания архитектуры нейросетей в байесовском ансамбле апостериорной (после обучения НСМ) фильтрации НСМ в ансамбле — осреднении результатов моделирования на отфильтрованном ансамбле.
Рецензенты:
Лобанов С.А., д.м.н., профессор кафедры охраны здоровья и безопасности жизнедеятельности, ФГБОУ ВПО «Башкирский государственный педагогический университет им. М. Акмуллы, г. Уфа;
Горбушина С.Н., д.п.н., профессор кафедры стандартизации и сертификации Уфимского государственного авиационного технического университета, г. Уфа.
Библиографическая ссылка
Горбатков С.А., Горбаткова Е.Ю. ИСПОЛЬЗОВАНИЕ БАЙЕСОВСКОЙ РЕГУЛЯРИЗАЦИИ МОДЕЛИ АНАЛИЗА УСЛОВИЙ И ОБРАЗА ЖИЗНИ ОБУЧАЮЩЕЙСЯ МОЛОДЕЖИ // Современные проблемы науки и образования. – 2015. – № 3. ;URL: https://science-education.ru/ru/article/view?id=18842 (дата обращения: 19.04.2024).