Создание систем контроля колёсных пар движущегося состава обусловлено необходимостью обеспечения безопасности и надёжности железнодорожного транспорта. Сравнительно недавно на железных дорогах ряда стран стали внедряться системы оптического контроля параметров колесных пар подвижного состава в движении [1–7].
Развитие систем бесконтактной диагностики движущихся колёсных пар основывается на разработке новых технических решенийс использованием современных достижений оптики, лазерной техники и информационных технологий. Большинство оптических систем размерного контроля движущихся колёсных пар основано на применении высокоскоростных цифровых камер. Однако применение цифровых камер ограничивается погодными условиями, особенно в зимних условиях таких стран, как, например, Россия. Кроме того, быстродействием и чувствительностью камеры ограничивается максимальная скорость движения, при которой осуществляется контроль. Российская система, получившая название «КОМПЛЕКС» [8], обеспечивает автоматический контроль геометрических параметров колёсных пар во время движения поезда, основанный на применении лазерных триангуляторов в режиме самосканирования. В работе [9] показано, что угловая скорость колеса, движущегося по рельсу, может измеряться методом, аналогичным способу определения крутящего момента цилиндрического вала путём измерения разности линейных скоростей в разнесённых точках на его вращающейся поверхности [10]. Информация об угловой скорости вращения колеса и линейной скорости его оси позволяет определить геометрический радиус колеса. Этот способ применим для контроля колёс с поверхностью катания аналогичной поверхности круглого цилиндра, что для железнодорожных колёс не выполняется, и в отсутствие проскальзывания при качении. Настоящая работа мотивирована проблемой развития методов оптического контроля колёсных пар движущегося состава на основе лазерных триангуляционных и доплеровских измерительных технологий.
Оптические методы размерного контроля колёс движущегося железнодорожного состава. Размерный контроль геометрических параметров железнодорожных колёс движущегося состава может быть обеспечен методами лазерной диагностики, в числе которых триангуляционные и лазерные доплеровские технологии являются наиболее адекватными проблеме.
Триангуляционный метод диагностики. Принцип работы триангуляционного измерителя иллюстрирует рис. 1. На пути движения колеса объективом формируется лазерный луч, который пересекается движущимся колесом. Точка пересечения лазерного луча с поверхностью катания колеса объективом 2 проектируется на позиционно-чувствительный фотоприёмник. Траектория перемещения проекции этой точки, получающаяся при движении колеса и регистрируемая позиционно-чувствительным фотоприёмником, определяет профиль поверхности катания колеса. Сигнал от позиционно-чувствительного приёмника фиксируется и обрабатывается сигнальным процессором.
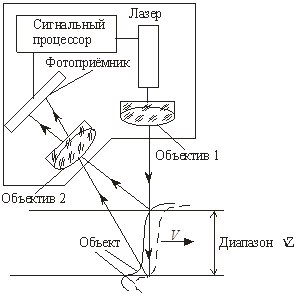
Рис. 1. Принцип работы лазерного триангуляционного измерителя
Триангуляционный метод размерного контроля колёс реализован в российской системе «КОМПЛЕКС» [8], разработанной Конструкторско–технологическим институтом научного приборостроения Сибирского отделения Российской академии наук.
Во время движения состава каждое из колёс параллельно и независимо сканируется двумя оптическими датчиками, один из которых установлен с внутренней стороны, а второй снаружи рельса. При прохождении колёсных пар в зоне контроля триангуляционные оптические датчики измеряют текущие расстояния до внешней и внутренней поверхностей каждого из колёс соответственно. В результате такого измерения формируются сигналы, несущие информацию о профилях колёс в сечениях, определяемых в координатном базисе, заданном положением датчиков. По восстановленному профилю вычисляются требуемые геометрические параметры. Внешний вид одного из вариантов системы «КОМПЛЕКС» приведен на рис. 2.
Рис. 2. Внешний вид системы «КОМПЛЕКС»
На железных дорогах России в настоящее время функционирует свыше 70 систем «КОМПЛЕКС», объединённых в единое информационное пространство. Обеспечивается высокая точность автоматических замеров в диапазоне скоростей движения поездов на участке контроля до 60 км/ч.
Лазерные доплеровские технологии контроля геометрических параметров железнодорожного колеса. Одно из направлений дальнейшего развития систем размерного контроля колёсных пар движущегося состава связано с возможностью применения лазерных доплеровских измерительных технологий. Лазерные доплеровские технологии помимо размерного контроля геометрических параметров позволяют получать информацию о радиусе и скорости проскальзывания колёс железнодорожных вагонов. Контроль скорости проскальзывания колеса локомотива позволяет оптимизировать вращающий момент, адаптируя энергетические параметры к условиям движения.
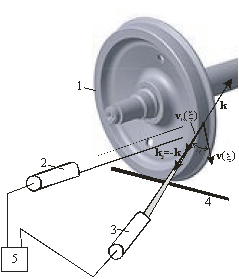
Рис. 3. Упрощённая структура системы лазерной доплеровской диагностики геометрии движущегося железнодорожного колеса
Рисунки 3 – 5 поясняют обсуждаемый способ дистанционного контроля профиля поверхности катания колеса и скорости проскальзывания [11]. На рис. 3 введены обозначения: 1 – колесо; 2 – измеритель скоростей 
и 
в двух точках поверхности колеса с известным относительным положением; 3 – лазерное устройство, измеряющее профиль поверхности катания; 4 – рельс; Выходы измерителей подключены к компьютеру 5. Колесо катится по рельсу в направлении оси х. Скорость движения оси колеса V и х–составляющие скорости движения его поверхности в двух точках измеряются оптическими методами (с использованием, например, лазерных доплеровских измерительных технологий).
a
b
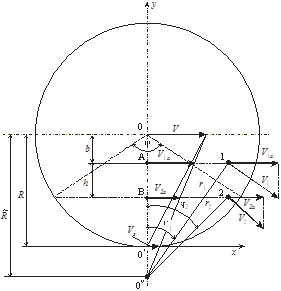
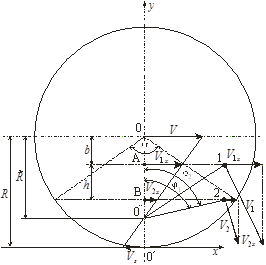
Рис. 4. Измерение геометрических и кинематических параметров колеса: a – вагона, b – локомотива.
Контур колеса на рис. 4 изображён окружностью с центром 0. В ситуации, когда проскальзывание отсутствует, точка 0¢ отображает в лабораторной системе отсчёта мгновенный центр (ось), относительно которого вращается колесо при качении по рельсу. Если же колесо катится с проскальзыванием, угловая скорость его уменьшается, и мгновенная ось вращения смещается в положение 0¢¢. На рисунке ось х направлена вдоль поверхности рельса, ось у проходит через точки 0 и 0¢.
Пусть в точках 1 и 2 одновременно измеряются локальные линейные скорости и , параллельные оси х. Проекция расстояния между точками 1 и 2 на ось у равна h. Для измеряемых скоростей и , согласно рисунку, имеем:
,
, (1)
где 
– мгновенная угловая скорость относительно мгновенной оси вращения 0¢¢; 
и 
– мгновенные радиусы вращения точек 1 и 2 относительно центра вращения 0¢¢; 
– угол между радиусом вращения и осью у; 
– угол между радиусом вращения и осью у.
Отсюда находится мгновенная угловая скорость как отношение разности линейных скоростей 
и h:
. (2)
Линейная скорость V движения центра вращения колеса 0 параллельна оси х и совпадает со скоростью движения буксы колеса. Скорость V равна произведению угловой скорости на мгновенный радиус 
. При наличии проскальзывания
. (3)
Если же проскальзывание отсутствует, скорость V определяется произведением угловой скорости 
на реальный геометрический радиус колеса R:
. (4)
Угловые скорости и связаны соотношением
, (5)
где 
– изменение угловой скорости вращения колеса, вызванное проскальзыванием. Знак «–» в (4) выбирается для колеса при проскальзывании или в режиме торможения. Знак «+» соответствует движению колеса локомотива, когда на ось колеса действует активный вращающийся момент. Если проскальзывание отсутствует, 
и 
. Радиус колеса R, как видно из рисунка 4, равен
. (6)
Расстояние 
равно расстоянию от точки 2 до поверхности рельса. Оно является известным и определяется при позиционировании зондирующего светового поля лазерного доплеровского измерителя скорости на поверхности колеса:
. (7)
Из (6) и (7) находится геометрический радиус колеса R:
. (8)
Учитывая связь полярного угла с угловой скоростью, 
, где 
– функция Хевисайда, измеренный радиус колеса можно представить как функцию полярного угла, непрерывную, 
, или дискретизированную, 
. Скорость проскальзывания 
находится как произведение угловой скорости на разность текущих значений мгновенного радиуса вращения 
и геометрического радиуса R:
. (9)
Ситуация, когда в лабораторной системе отсчёта определяется радиус и скорость проскальзывания колеса, к которому приложен крутящий момент, отображена на рис. 4b. Это соответствует движению колеса локомотива. Как видно из рис. 4b, значение измеряемого радиуса колеса больше или равно значению мгновенного радиуса вращения, 
, и скорость проскальзывания меняет знак. При этом мгновенный центр вращения оказывается смещённым по оси у внутрь круга, ограниченного контуром колеса. Измерение скорости проскальзывания и радиуса ведущих колёс локомотива даёт возможность оптимально управлять крутящим моментом, приложенным к оси колеса, что повышает энергосбережение при эксплуатации. В этом случае измерения выполняются в системе отсчёта локомотива.
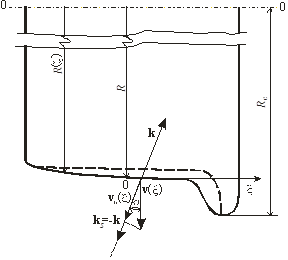
Рис. 5. Лазерная доплеровская диагностика профиля поверхности катания железнодорожного колеса
Метод измерения профиля поверхности катания поясняется рисунком 5. На этом рисунке показан гребень и профиль поверхности катания (в разрезе). Радиус гребня колеса – 
, где 
– высота гребня. Прокат по кругу катания представляет собой разность между штатным (исходным) и изменённым в процессе эксплуатации профилем поверхности катания. Прокат по кругу катания выше предельного, отмеченного на рис. 5 штриховой линией, является дефектом, при котором запрещена эксплуатация колёсной пары. R обозначает радиус колеса в плоскости круга катания; 0 – точка соответствует нулю на координатной оси x, ортогональной радиусу 
R(x) – радиус колеса в плоскости x, параллельной плоскости среднего круга катания и пересекающей профиль в точке с координатой x. Для контроля профиля на поверхность катания направляется лазерный пучок с волновым вектором 
. Свет рассеивается в области пересечения лазерного пучка с поверхностью. На рисунках 3 и 5 эта малая область обозначается точкой, координата которой x. В рассеянном световом поле выделяется пучок с волновым вектором 
. Частота рассеянного света отличается от частоты падающего пучка на величину доплеровского частотного сдвига, который определяется скалярным произведением вектора скорости на разность волновых векторов рассеянного и падающего световых пучков:
, (11)
где 
– скорость движения поверхности катания в точке с координатой x; 
– доплеровский сдвиг частоты, 
; a – угол между направлением скорости и вектором 
.
На рис. 5 для определённости направление выделенного рассеянного пучка выбрано противоположным лазерному пучку 
. В этом случае формула (11) для доплеровского сдвига частоты принимает вид:
, (12)
где 
– волновое число; l – длина волны лазерного излучения; 
– радиус колеса в сечении x поверхности катания. Это сечение параллельно плоскости круга катания; – измеренная угловая скорость колеса, связанная с линейной скоростью и радиусом колеса 
.
Измерение доплеровского частотного сдвига выполняется устройством 3 (рис. 3). Это устройство представляет собой лазерный доплеровский измеритель скорости, который может быть совмещён с лазерным триангуляционным измерителем. При движении состава происходит самосканирование точки пересечения лазерного пучка с поверхностью катания по оси x. Из (12) находим радиус поверхности катания в сечении 
:
. (13)
Согласно формуле (13), профиль поверхности катания определяется как произведение радиуса круга катания колеса 
на доплеровский сдвиг частоты 
в свете, рассеянном в точке 
траектории пересечения лазерного луча с поверхностью катания, нормированный на доплеровский сдвиг частоты в свете, рассеянном на поверхности катания в точке, соответствующей радиусу круга катания. Информация о профиле поверхности катания получается на основе частотных измерений, что обеспечивает повышенную помехоустойчивость. Измерение линейных скоростей в точках на поверхности колеса производится с применением доплеровских измерительных технологий на основе полупроводниковых лазеров. Реализация этого способа на железнодорожном транспорте позволит оперативно выявлять дефектные колёса, тем самым повышая безопасность.
Заключение
Рассмотрены методы размерного контроля колёс движущегося железнодорожного состава, основанные на оптических триангуляционных и доплеровских технологиях. Лазерные триангуляционные технологии к настоящему времени наиболее проработаны и реализованы в серийных российских системах «КОМПЛЕКС», обеспечивающих контроль геометрических параметров колёс при скорости до 60 км/час. Лазерные доплеровские измерительные технологии могут быть полезны для контроля не только геометрических параметров, но и динамических, таких как, например, скорость проскальзывания колёс. Возможность применения лазерных доплеровских технологий для создания систем размерного контроля колёс движущегося железнодорожного состава заслуживает внимания и развития.
Рецензенты:
Лабусов В.А. д.т.н., заведующий лабораторией оптических информационных систем Института автоматики и электрометрии СО РАН, г. Новосибирск;
Арбузов В.А., д.т.н., ведущий научный сотрудник Института теплофизики СО РАН, профессор Новосибирского государственного технического университета, г. Новосибирск.
Библиографическая ссылка
Сотников В.В., Дубнищев Ю.Н., Сотников В.В., Чугуй Ю.В. ЛАЗЕРНЫЕ МЕТОДЫ РАЗМЕРНОГО КОНТРОЛЯ КОЛЁСНЫХ ПАР ПРИ ДВИЖЕНИИ ЖЕЛЕЗНОДОРОЖНОГО СОСТАВА // Современные проблемы науки и образования. – 2015. – № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18779 (дата обращения: 19.04.2024).