Постановка задачи
Как известно, обратная задача динамики состоит в определении законов изменения сил по заданным движениям рабочей точки. Рассмотрим шестизвенный манипуляционный робот, механика которого описана в [4].
Представим уравнения движения «безынерционного» манипуляционного робота в виде [2, 5]:
(1)
где 
– 6-мерный вектор обобщённых координат; 
В – матрица [6x6] постоянных коэффициентов;
и – вектор управления.
Требуется найти аналитическое выражение вектора и так, чтобы заданное s – мерное гладкое многообразие 
(2)
было интегральным для (1).
Рассмотрим следующую задачу. Пусть требуется перенести предмет манипулирования из одного заданного положения в другое. В программу введён закон движения рабочей точки O6 схвата:
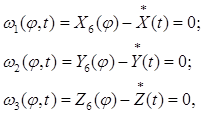(3)
где X6(φ), Y6(φ), Z6(φ) – координаты рабочей точки О6 схвата;
– заданные законы изменения координат рабочей точки О6.
Если законы изменения выбрать в виде [1]:
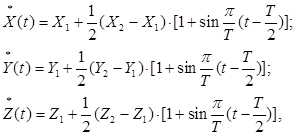(4)
где X1,Y1,Z1 – начальные, а X2,Y2,Z2 – конечные значения координат рабочей точки О6;
Т – время перемещения, то движение схвата начнётся и закончится с нулевой скоростью.
Алгоритм управления
Как известно, на основе решения обратных задач динамики [3, 5], вектор управления определяется выражением:
(5)
где 
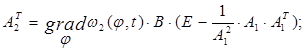
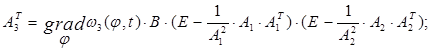
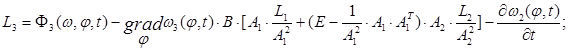
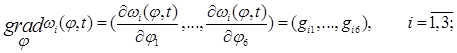
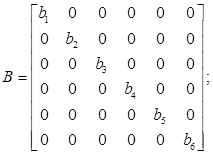b1=b2=0,045; b3=b4=0,052;b5=b6=0,058;
E – единичная матрица размера [3x3];
T – символ транспонирования;
Числовые задачи
Зададим закон движения рабочей точки схвата О6 в виде:
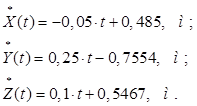(6)
Пусть в начальный момент времени рабочая точка схвата О6 находится на программной траектории, и её положение определяется координатами:
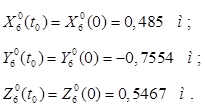
При этом обобщённые координаты имеют значения: φ10=φ1(0)=-1 рад.;
φ20=φ2(0)=1 рад.; φ30=φ3(0)=0,5 рад.; φ40=φ4(0)=0 рад.; φ50=φ5(0)=-1 рад.; φ60=φ6(0)=0 рад.
Изменения во времени значений: Ui(t), i=1,…,5; φj(t), j=1,…,5; X06(t), Y06(t), Z06(t) показаны на рис. 1 (а, б и в).
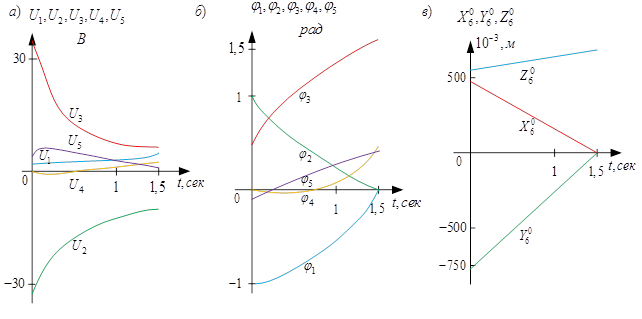
Рис. 1. Изменение управленияUi(t) (а), обобщённых координатφj(t)(б) и координат схватаX06(t), Y06(t), Z06(t) (в) по заданному закону во времени
Анализ полученных результатов показывает, что изменения координат рабочей точки происходят по прямолинейному закону.
Движение при наличии начальных отклонений.
Пусть в начальный момент времени обобщённые координаты манипулятора равны:
φ10=-0,92 рад; φ20=1,2 рад; φ30=0,8 рад;
φ40=0,025 рад; φ50=0,085 рад; φ60=0 рад.
Координаты рабочей точки схвата манипулятора имеют следующие значения:
Зададим функции 
в виде:
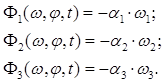
Изменения во времени значений: Ui(t), i=1,…,5; φj(t), j=1,…,5; X06(t), Y06(t), Z06(t) показаны на рис. 2 (а, б и в) при αk=1 и αk=4, k=1,…,3.
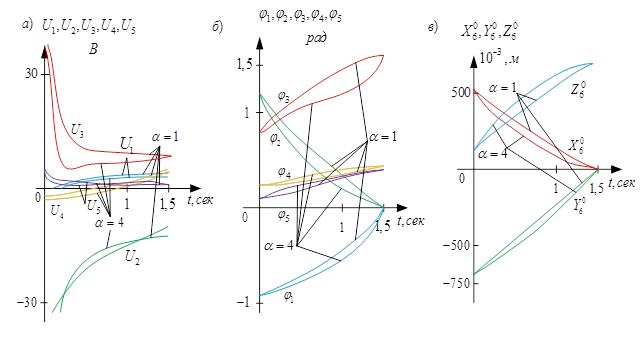
Рис. 2. Изменение управления Ui(t) (а), обобщённых координат φj(t) (б) и координат схватаX06(t), Y06(t), Z06(t) (в) при движении при наличии начальных отклонений
Процессы показывают, что чем больше α, тем сильнее отличатся закон движения от прямолинейного.
Пусть требуется перенести рабочую точку схвата О6 из одной точки пространства в другое. Заданы координаты этих точек:
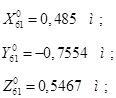
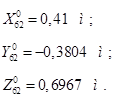
Чтобы движение начиналось и заканчивалось с нулевой скоростью, закон движения зададим следующим образом, Т=1,5 сек.
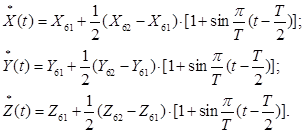
Изменения во времени значений: Ui(t), i=1,…,5; φj(t), j=1,…,5; X06(t), Y06(t), Z06(t) показаны на рис.3 (а, б и в).
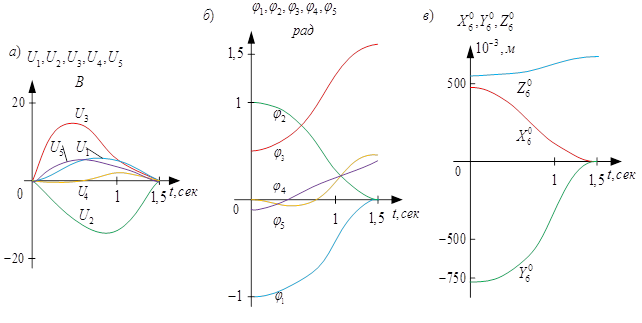
Рис. 3. Изменение управления Ui(t) (а), обобщённых координат φj(t) (б) и координат схватаX06(t), Y06(t), Z06(t) (в) при движении, начинающемся и заканчивающемся с нулевой скоростью
Зависимости показывают, что движение начинается и заканчивается с управлением, равным нулю. При этом касательные к графикам обобщённых координат и координат рабочей точки манипулятора в начальный и конечный момент времени горизонтальны.
Таким образом, решается обратная задача динамики применительно к положению схвата манипуляционного робота в процессе его перемещения в пространстве состояний.
Рецензенты:
Присмотров Н. И., д.т.н., профессор ФГБОУ ВПО «Вятский государственный университет», г. Киров;
Хорошавин В. С., д.т.н., профессор ФГБОУ ВПО «Вятский государственный университет», г. Киров.
Библиографическая ссылка
Лалетин В.И., Рычков В.В., Сбоев В.М. ПРОГРАММНОЕ УПРАВЛЕНИЕ ДВИЖЕНИЯМИ МАНИПУЛЯЦИОННОЙ СИСТЕМЫ // Современные проблемы науки и образования. – 2015. – № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18776 (дата обращения: 10.10.2024).