Рост автотранспортного парка сопровождается резким увеличением интенсивности движения на автомобильных дорогах и городских улицах. Транспортная инфраструктура, в свою очередь, не может развиваться в таком же высоком темпе. Строительство новых и реконструкция существующих дорог является дорогим и трудоёмким процессом, требующим значительного времени. Предотвратить или, по крайней мере, уменьшить перегрузку транспортной сети возможно за счет более эффективного использования имеющихся дорог в сочетании с использованием современных методов управления дорожным движением.
В современных адаптивных системах управления дорожным движением в реальном времени, как правило, оптимизируется некоторый функционал [1, 5]:
![]() , (1)
, (1)
где X – вектор состояния управляемых объектов; U – вектор соответствующих управляющих воздействий.
Чаще всего функционал Q(X,U) принимает форму индекса потерь DI(xi,ui) , а соответствующая задача оптимального управления имеет вид:
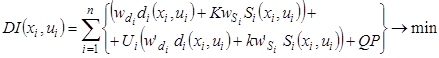 , (2)
, (2)
![]() ; (3)
; (3)
где di(xi,ui) - задержка на связи i при состоянии транспортного потока xi и управлении ui; K - фактор штрафа остановок транспортных средств; Si(xi,ui) - количество остановок на связи i; wdi, wSi - весовые коэффициенты связи i соответственно для задержки и остановки, как правило, соответствуют дополнительному расходу топлива; Ui - бинарная переменная, которая принимает значение «1», если для связи установлены дополнительный веса w'di, w'Si, в противном случае «0»; QP - штраф очереди; umin и umax - нижние и верхние ограничения на управляющие воздействия.
Постановка задачи управления (2-3) в основном рассчитана на свободные условия движения. В условиях насыщенного движения предотвращение или ликвидация поникших транспортных заторов производится путем установки весовых коэффициентов функции (2) экспертным способом с последующей корректировкой в процессе эксплуатации в зависимости от реальных условий. Качество управления в этом случае во многом зависит от опыта транспортного инженера и его квалификации [1].
Структурная схема управления в условиях насыщенного движения
Не стационарность состояния транспортных потоков в условиях насыщенного движения [2], и как следствие, невозможность получения закрытой формы модели очереди и задержки транспортных средств диктует необходимость использования управления с прогнозирующей моделью (Model Predictive Control) [4]. Основой управления с прогнозирующей моделью является схема управления динамическими объектами по принципу обратной связи (рисунок 1). На каждом шаге управления решается задача оптимального управления на прогнозируемый период ks (именуемый горизонтом прогноза) и реализуется на горизонте управления kc, следующим образом:
1) рассматривается математическая модель объекта управления, начальными условиями для которой служит его текущее состояние. При заданном программном управлении выполняется моделирование состояния объекта на горизонте прогноза ks;
2) выполняется оптимизация программного управления, целью которого служит приближение регулируемых переменных прогнозирующей модели к оптимальным значениям на горизонте прогноза. Оптимизация осуществляется с учётом ограничений, накладываемых на управляющие и регулируемые переменные;
3) на временном шаге kc, именуемом горизонтом управления и составляющем фиксированную малую часть горизонта прогноза ks, реализуется найденное оптимальное управление и осуществляется измерение (или оценка по измеренным переменным) фактического состояния объекта на конец шага управления;
4) горизонт прогнозирования смещается на горизонт управления ks и задача оптимального управления решается вновь (повторяются п. 1 – 3).
Горизонт прогноза ks и горизонт управления kc связаны соотношением:
![]() , (1)
, (1)
где n – достаточно большое целое число.
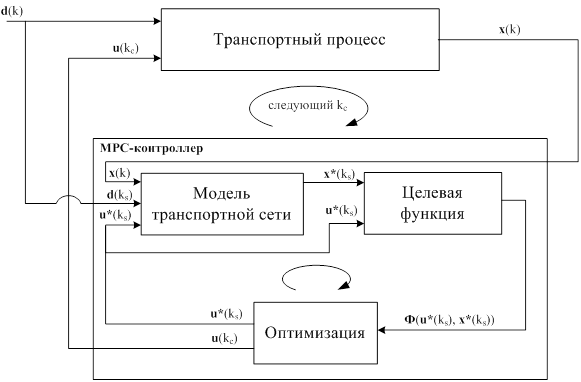
Рис.1. Структурная схема управления с прогнозирующей моделью
Синтез управления с прогнозирующей моделью включает следующие операции:
-
постановку задачи оптимального управления и ограничений на управляемые переменные u(k) и состояние объекта x(k);
-
выбор модели транспортной сети и величины шагов горизонта управления и прогноза;
-
выбор технологии оптимизации, обеспечивающей решение задачи оптимального управления в пределах допустимого запаздывания.
Синтез системы управления насыщенными транспортными потоками
Проблемы управления насыщенными транспортными потоками принципиально отличается от проблем управления при свободном движении, а в транспортных сетях проблема осложняется из-за невозможности локализовать режим перенасыщения в пределах отдельного перекрестка, первоначально явившегося источником возникновения затора. Отрицательную роль играет фактор связности между отдельными перекрестками – неограниченно возрастающая очередь на одном перекрестке блокирует транспортные потоки предыдущего по ходу движения перекрестка, который, в свою очередь, может заблокировать работу смежных перекрестков и т.д. Указанный процесс может полностью заблокировать на длительное время движение в отдельной области транспортной сети.
В связи с этим, основной задачей систем управления в условиях насыщенного движения должно являться предотвращение случаев возникновения транспортных заторов, а при возникновении – максимально быстрая ликвидация их последствий. Естественный путь решения задачи предотвращения заторов состоит в устранении причин, вызвавших перегрузку в узком месте сети. Поскольку управляющая система не в состоянии увеличить пропускную способность соответствующего перекрестка, единственным путем снижения риска возникновения заторов является своевременное ограничение количества транспорта, прибывающего в опасное сечение сети [5, 8].
В общем случае, причиной образования транспортного затора является возникновение остаточной очереди вследствие превышения количества вошедших в связь автомобилей ![]() числа ее покинувших
числа ее покинувших ![]() . Задачу управления светофорными объектами как задачу максимизации загрузки сети:
. Задачу управления светофорными объектами как задачу максимизации загрузки сети:
![]() ; (2)
; (2)
при ограничениях:
![]() ; (3)
; (3)
![]() , (4)
, (4)
![]() ; (5)
; (5)
где ![]() – суммарная интенсивность отъезда в районе управления,
– суммарная интенсивность отъезда в районе управления, ![]() ;
;![]() – управляющие воздействия (множество длительностей сигналов управления на светофорных объектах);
– управляющие воздействия (множество длительностей сигналов управления на светофорных объектах);![]() – интенсивность входящих в транспортную связь транспортных потоков;
– интенсивность входящих в транспортную связь транспортных потоков; ![]() – интенсивность исходящих с транспортной связи транспортных потоков;
– интенсивность исходящих с транспортной связи транспортных потоков; ![]() ,
, ![]() – соответственно верхние и нижние ограничения на длительность сигналов управления;
– соответственно верхние и нижние ограничения на длительность сигналов управления; ![]() – максимальное удаление от стоп-линии фронта очереди в цикле регулирования, м;
– максимальное удаление от стоп-линии фронта очереди в цикле регулирования, м; ![]() – длина транспортной связи
– длина транспортной связи
Формирование транспортных потоков внутри транспортной сети определяется формулой:
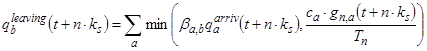 ; (6)
; (6)
где ![]() – поток насыщения связи a;
– поток насыщения связи a; ![]() – длительность разрешающего сигнала на связи a пересечения
– длительность разрешающего сигнала на связи a пересечения ![]() ;
; ![]() – длительность светофорного цикла на пересечении n.
– длительность светофорного цикла на пересечении n.
Аналитические зависимости для вычисления максимального удаления от стоп-линии фронта очереди в цикле регулирования ![]() можно найти в работе [9], а методику оценки состояния транспортных потоков в работе [7].
можно найти в работе [9], а методику оценки состояния транспортных потоков в работе [7].
Как видим, поставленная задача оптимизации режимов работы светофорных объектов в сети в условиях насыщенного движения (2 – 5) является задачей нелинейного целочисленного программирования с ограничениями как линейного, так и нелинейного вида.
В практике управления дорожного движения для решения задач указанного вида чаще всего применяется генетический алгоритм. В основу работы генетического алгоритма заложена имитация процесса эволюции живых организмов, представляющая собой итерационный процесс (имитация смены поколений), работающий одновременно с несколькими взаимодействующими решениями. Подробное описание работы генетического алгоритма можно найти в литературе [1, 3].
Оценка эффективности управления на микроскопической модели
Для оценки эффективности предложенного метода управления была создана микроскопическая имитационная модель в программе SUMO, включающая 5 регулируемых пересечений. Реализация управления с прогнозирующей моделью выполнено на языке программирования Python с использованием модуля TraCI [6], для решения задачи оптимизации (2-5) использовался модуль OpenOpt. В качестве базового алгоритма управления принят общеизвестный метод адаптивного управления – алгоритм поиска разрыва в потоке (в зарубежной литературе именуемый «actuated traffic control»). На пересечениях A, B и C пропуск автомобилей производится в четыре фазы (с выделенными фазами для левых поворотов), а на пересечении D предполагалось наличие пятой, выделенной пешеходной фазы продолжительностью 20 с. При использовании базового метода наблюдалось образование транспортного затора на связи С-D, который в последствии приводил к блокированию остальных связей на маршруте движения A-B-C-D.
При управлении по предложенной методике образование затора не происходило, при этом наблюдались незначительные колебания плотности транспортного потока в районе 20 авт/км в расчете на одну полосу движения (сплошная линия на рисунке 2).
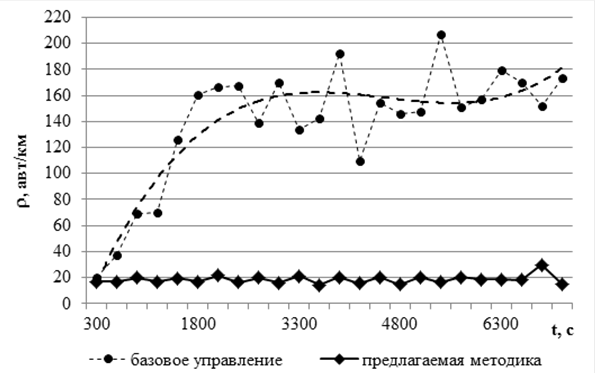
Рис.2. Динамика плотности транспортного потока на связи В – С
Благодаря отсутствию транспортного затора суммарная задержка транспортных средств на перегонах маршрута движения A – B – C – D сократилась в 2,5 – 4 раза (рисунок 3).
Среднее время движения транспортных при базовом способе управления составила 234,63 с, а при установке режимов работы светофоров, рассчитанных по предлагаемой методике – 211,67 с. Среднее время ожидания разрешающего сигнала соответственно уменьшилось со 118,49 с до 101,96 с.
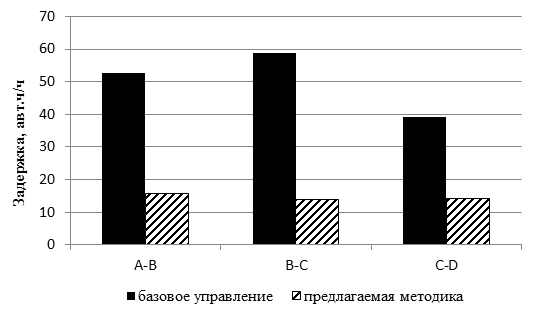
Рис.3. Суммарная задержка на маршруте движения A – B – C – D
Заключение
Управление магистральной улицей в условиях насыщенного движения может быть эффективно реализовано при использовании управления с прогнозирующей моделью. При этом задача оптимального управления формулируется как задача максимизации объемов движения при соблюдении баланса транспортного спроса и предложения, отсутствия заблокированных транспортных связей и ограничениях на длительность разрешающих сигналов. Проведенная оценка предложенного способа управления на микроскопической модели показала его эффективность и способность предотвращать возникновение транспортных заторов.
К недостаткам приведенного подхода к управлению насыщенными транспортными потоками следует отнести ограниченность воздействий. Так при достаточно долгом существовании предзаторовой ситуации произойдет переполнение всех второстепенных въездов, что делает невозможным нахождение решения задачи (2), удовлетворяющее условию (5). Разрешением указанной проблемы может явиться постановка и решение задачи балансировки транспортного спроса и предложения между смежными магистралями.
Рецензенты:
Родионов Ю.В., д.т.н., профессор кафедры «Эксплуатация автомобильного транспорта» ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза;
Бажанов А.П., д.т.н., профессор кафедры «Геотехника и дорожное строительство» ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза.
Библиографическая ссылка
Орлов Н.А. СЕТЕВОЕ УПРАВЛЕНИЕ СВЕТОФОРНЫМИ ОБЪЕКТАМИ В УСЛОВИЯХ НАСЫЩЕННОГО ДВИЖЕНИЯ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18707 (дата обращения: 12.03.2026).



