Рассматриваемые в работе сателлитные Оже-переходы (СОП) весьма близки по характеру к двойным Оже-переходам (ДОП) [1,2], в которых при автоионизационном распаде внутренней атомной вакансии испускается сразу два электрона с непрерывно распределенной между ними энергией перехода. В СОП же лишь один электрон q вполне определенной энергии излучается в непрерывный спектр, а второй возбуждается на дискретный уровень nl двукратного иона. Таким образом, конечное состояние характеризуется тремя вакансиями f1, f2, f3, электроном на возбужденном дискретном уровне nl и Оже-электроном q в непрерывном спектре, рис 1. В таком переходе участвуют, как минимум, три атомных электрона. Поскольку часть энергии перехода затрачивается на возбуждение второго электрона на уровень nl, то кинетическая энергия Оже-электрона уменьшается на соответствующую величину, что приводит к появлению дополнительных (сателлитных) линий в Оже-спектрах. Последующий распад таких резонансов приводит к появлению дополнительных линий [4,5] в спектрах и структур в сечениях.
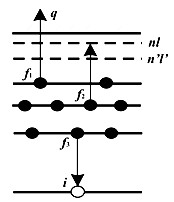
Рис. 1. Сателлитный Оже-переход
Рассчитаны энергии и вероятности более 450 СОП вида ![]()
![]()
![]() и
и ![]()
![]()
![]() в Kr. Характеристики этих переходов полезны при интерпретации экспериментальных спектров флюоресценции и сечений фотоионизации, полученных методом ФИФС [4] при фотовозбуждении Kr в области порога ионизации его 3d-оболочки. Возбуждение короткоживущих резонансов типа
в Kr. Характеристики этих переходов полезны при интерпретации экспериментальных спектров флюоресценции и сечений фотоионизации, полученных методом ФИФС [4] при фотовозбуждении Kr в области порога ионизации его 3d-оболочки. Возбуждение короткоживущих резонансов типа ![]() и
и ![]() одним фотоном (по сути, двойная фотоионизация с возбуждением третьего электрона на дискретный уровень) может происходить напрямую за счет корреляционных взаимодействий. Однако при этом можно выделить такие реальные промежуточные состояния, разрешенные законом сохранения энергии и правилами отбора, через которые наиболее вероятно идут последовательно процессы фотовозбуждения и автоионизации. Таким образом, имеет смысл исследовать двухступенчатую траекторию, первая ступень которой есть фотоионизация 3d-оболочки, а вторая – СОП указанного вида.
одним фотоном (по сути, двойная фотоионизация с возбуждением третьего электрона на дискретный уровень) может происходить напрямую за счет корреляционных взаимодействий. Однако при этом можно выделить такие реальные промежуточные состояния, разрешенные законом сохранения энергии и правилами отбора, через которые наиболее вероятно идут последовательно процессы фотовозбуждения и автоионизации. Таким образом, имеет смысл исследовать двухступенчатую траекторию, первая ступень которой есть фотоионизация 3d-оболочки, а вторая – СОП указанного вида.
Теоретическая основа
Вероятность безызлучательного перехода между начальным ![]() и конечным
и конечным ![]() состоянием с энергиями
состоянием с энергиями ![]() и
и ![]() в первом порядке ТВ по межэлектронному взаимодействию
в первом порядке ТВ по межэлектронному взаимодействию ![]() определяется известным выражением:
определяется известным выражением:
![]() .
.
На этой основе в рамках методического подхода [1] с использованием нестационарной многочастичной теории возмущений (ТВ) в формализме вторичного квантования построена теория двойного Оже-эффекта [2,3], физический механизм которого аналогичен таковому для рассматриваемых СОП. Использован базис нерелятивистских хартри-фоковских волновых функций (ВФ), поэтому взаимодействие ![]() равно остаточному взаимодействию
равно остаточному взаимодействию ![]() .
.
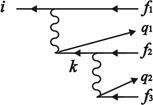
Рис. 2. Диаграмма Фейнмана для СОП
При построении ВФ конечных состояний определенного терма использована следующая схема сложения моментов: ![]() (в приближении LS-связи). В низшем неисчезающем порядке ТВ полная амплитуда СОП может быть представлена суммой девяти парциальных амплитуд [2,3], фейнмановская диаграмма одной из которых представлена на рис. 2. Угловые и спиновые множители парциальных амплитуд содержат 3
(в приближении LS-связи). В низшем неисчезающем порядке ТВ полная амплитуда СОП может быть представлена суммой девяти парциальных амплитуд [2,3], фейнмановская диаграмма одной из которых представлена на рис. 2. Угловые и спиновые множители парциальных амплитуд содержат 3![]() коэффициенты и δ-символы Кронекера. Условия, при которых они отличны от нуля, и четность состояний определяют правила отбора для рассматриваемых переходов.
коэффициенты и δ-символы Кронекера. Условия, при которых они отличны от нуля, и четность состояний определяют правила отбора для рассматриваемых переходов.
Основные результаты
Проведен расчет вероятностей и энергий более 450 СОП вида 3d-1[2D]→
4s-14p-2[4P, 2D] nl[LS] +q и 3d-1[2D]→4p-3[4S, 2P, 2D] nl[LS] +q в Kr со значениями главного квантового числа n=1,2,...,9. Поскольку с ростом n и l вероятность переходов значительно убывает, мы ограничились значениями орбитального момента l=0,1,2,3. Результаты расчета приведены в таблицах 1-5. Для сокращения объема таблиц данные по ряду переходов
с Г<1.0 (мкэВ) опущены, но включены в суммарные значения ширины. Приведенные энергии εq большинства переходов определены на основе экспериментальных данных [7,8].
Таблица 1
Энергия ε (эВ) и ширина Г (мкэВ) СОП 3d-1[2D]→4s-14p-2[2D] nl[LS] +q.
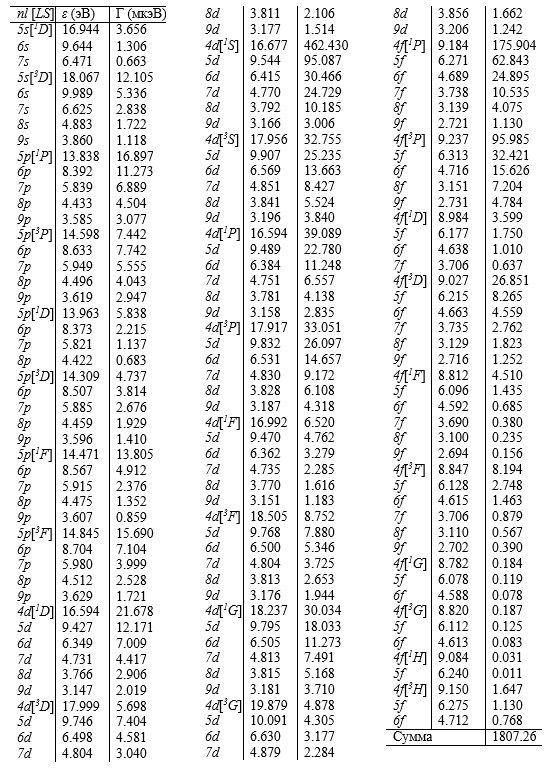
Таблица
Энергия ε (эВ) и ширина Г (мкэВ) СОП 3d-1[2D]→4s-14p-2[4P] nl[LS] +q.

Таблица 3
Энергия ε (эВ) и ширина Г (мкэВ) СОП 3d-1[2D]→ 4p-3[2D] nl[LS] +q
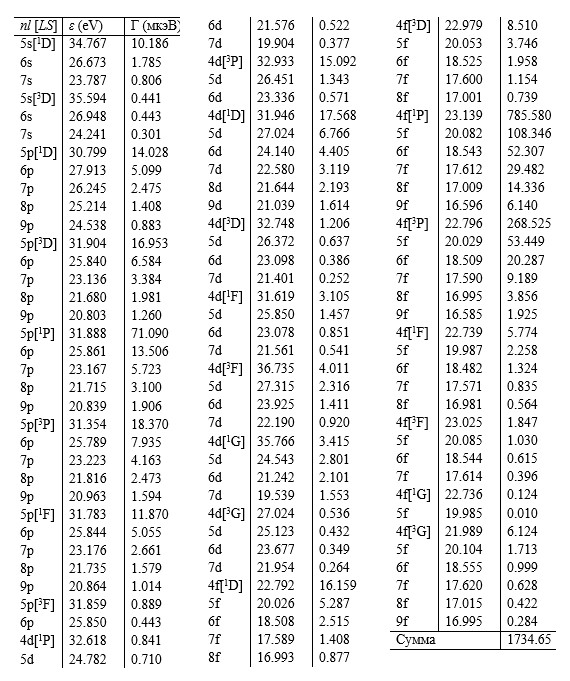
Таблица 4
Энергия ε (эВ) и ширина Г (мкэВ) СОП 3d-1[2D]→ 4p-3[2P] nl[LS] +q
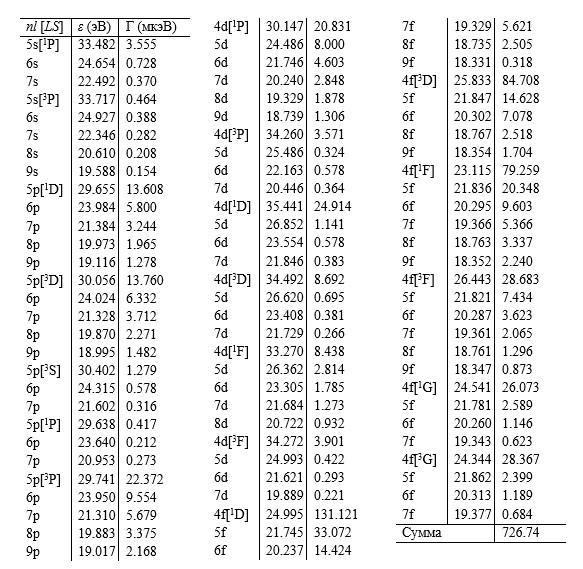
Таблица 5
Энергия ε (эВ) и ширина Г (мкэВ) СОП 3d-1[2D]→ 4p-3[4S] nl[LS] +q

По данным таблиц видно, что среди множества рассчитанных наиболее вероятными являются переходы в состояния 4s-14p-2[2D]4d[1S], 4p-3[2D]4f[1P], 4p-3[2P]4f[1D] и 4p-3[2D]4f[3P]. Это обусловлено сравнительно большими значениями кулоновских матричных элементов, входящих в парциальные амплитуды, при малых значениях энергетических знаменателей, что отражает сильное смешивание указанных состояний с начальным 3d-1[2D].
Наибольший вклад в сумму Гic дают переходы в состояния 4s-14p-2[2D] и 4p-3[2D] конечного ионного остова того же терма, что и начальное состояние 3d-1[2D]. Наименее вероятны переходы в квартетные состояния 4s-14p-2[4P] и 4p-3[4S], когда оба возбуждаемых электрона, nl и q, имеют параллельные спины.
Приведем здесь еще и суммарные по n=1,2,...,9 и l=0,1,2,3 абсолютные Гic (мкэВ) и относительные η=Гic/Гtot ширины СОП из 3d-1[2D], приводящие к ионным остовам:
4s-14p-2[4P] Гic= 222.124 η =5; 4s-14p-2 [2D] Гic=1807.262 η =40;
4p-3 [4S] Гic= 49.695 η =1; 4p-3 [2P] Гic=726.738 η =16;
4p-3 [2D] ГGic=1734.648 η =38. сумма Гtot=4540.467 η =100
Экспериментальное значение полной ширины Г3d состояния 3d-1[2D], к сожалению, не известно. Ее значение оценено по литературным данным следующим образом. Предполагается, что полная ширина состояний ![]() и
и ![]() примерно равна полной ширине высоковозбужденных резонансов
примерно равна полной ширине высоковозбужденных резонансов ![]() , а именно, 98±12 мэВ. Эксперимент высокого разрешения [8] показал меньшее значение ширины резонансов при возрастании
, а именно, 98±12 мэВ. Эксперимент высокого разрешения [8] показал меньшее значение ширины резонансов при возрастании ![]() , а именно от 83±1 мэВ для
, а именно от 83±1 мэВ для ![]() до 75±8 мэВ для
до 75±8 мэВ для ![]() и от 83±2 мэВ для
и от 83±2 мэВ для ![]() до 68±8 мэВ для
до 68±8 мэВ для ![]() . Полагая, что полная ширина Г3d=70 мэВ, суммарная ширина Гtot всех исследованных переходов составляет около 6.5% от Г3d.
. Полагая, что полная ширина Г3d=70 мэВ, суммарная ширина Гtot всех исследованных переходов составляет около 6.5% от Г3d.
На основе рассчитанных ширин и энергий переходов, приведенных в таблицах 1-5, построены модели электронного спектра для рассмотренных групп переходов, а также модель суммарного спектра (рис. 3). Для этого проведено “размазывание” рассчитанных ширин ![]() каждого перехода с энергией
каждого перехода с энергией ![]() по Лоренцу,
по Лоренцу, ![]() , где
, где ![]() численно равна площади под кривой Лоренца,
численно равна площади под кривой Лоренца, ![]() соответствует энергетическому положению пика,
соответствует энергетическому положению пика, ![]() - ширина пика на его полувысоте. Параметр
- ширина пика на его полувысоте. Параметр ![]() может быть подобран соответственно разрешению эксперимента.
может быть подобран соответственно разрешению эксперимента.
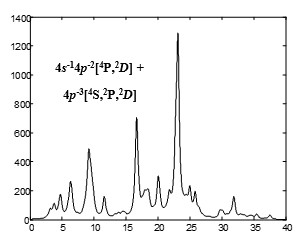
Рис.3. Модельный спектр СОП 3d-1→
4s-14p-2[4P,2D] nl[LS] +q и 3d-1→ 4p-3[4S,2D,2D] nl[LS] +q при σ =0.5 на по данным таблиц 1-5
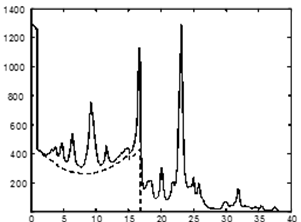
Рис. 4. Модельный спектр рис.3 на подложке непрерывного спектра от ДОП (штриховая линия - - -)
На основе полученных результатов, а также проведенного ранее расчета энергетического спектра электронов при двойном Оже-распаде 3d-вакансии в Kr [NN] можно построить модельный электронный спектр (рис.4), порождаемый при распаде 3d-вакансии в Kr, путем наложения дискретного спектра СОП (рис.3, Сумма) и подложки непрерывного спектра в области (0–18 эВ) от ДОП ([3], штриховая линия - - -). Отметим, что подложка меняет как высоту низкоэнергетических пиков, так и их форму.
Рецензенты:
Гриняев С.Н., д.ф.-м.н., профессор, кафедра теоретической и экспериментальной физики, Физико-технический институт, Научно-исследовательский Томский политехнический университет, г. Томск;
Шаповалов А.В., д.ф.-м.н., профессор, зав. кафедрой теоретической физики, физический факультет, Научно-исследовательский Томский государственный университет, г. Томск.
Библиографическая ссылка
Килин В.А., Килин Р.Ю. САТЕЛЛИТНЫЕ ОЖЕ-ПЕРЕХОДЫ В KRII // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18696 (дата обращения: 12.03.2026).



