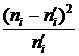Изучение математики, безусловно, основано на решении различного рода задач. Целью математического образования является получение математических знаний и выработка умений применять эти знания либо в решении прикладных задач, либо в строительстве и перестройке самого постоянно развивающегося здания математики. Целесообразность построения обучения математике посредством прикладных задач и является темой нашего исследования.
Поскольку научить алгоритмам решения всех задач, встречающихся специалисту в его работе, невозможно, то важно выработать культуру мышления, умение творчески подходить к решению возникающих задач. Таким образом, имеется тенденция усиления прикладной направленности курса математики и одновременно повышения уровня фундаментальной математической подготовки для дальнейшего успешного изучения смежных дисциплин [2]. На практике чаще всего решаются стандартные, алгоритмические задачи, позволяющие отработать основные понятия изучаемой темы. Рассмотрим понятие задачи прикладной направленности на примере задачи в строительстве, заметим, что в качестве задачной ситуации в ней выступает некая модель профессиональной ситуации, в которой по известным характеристикам профессионального объекта или явления надо найти другие его характеристики или свойства [7]. Разрешение или исследование представленной профессиональной ситуации способствует развитию у студента определенных профессиональных качеств. Наличие данных качеств способствует воспитанию конкурентоспособного специалиста, отлично выполняющего свою работу и полезного для общества.
Сформулируем требования, предъявляемые к задачам прикладного характера, используемым в рамках математической подготовки будущего строителя:
1) задача должна описывать ситуацию, возникающую в профессиональной деятельности инженера-строителя;
2) в задаче должны быть неизвестные характеристики некоторого профессионального объекта или явления, которые надо исследовать субъекту по имеющимся известным характеристикам с помощью средств математики;
3) решение задач должно способствовать прочному усвоению математических знаний, приемов и методов, являющихся основой профессиональной деятельности инженера-строителя;
4) задачи должны обеспечить усвоение взаимосвязи математики с общетехническими и специальными дисциплинами;
5) содержание задачи и ее решение требуют знаний по специальным предметам;
6) содержание профессионально ориентированной математической задачи определяет пропедевтический этап изучения понятий специальных дисциплин;
7) решение задач должно обеспечивать математическое и профессиональное развитие личности инженера-строителя [3].
Приведем примеры такого рода задач, в которых используется математический аппарат и которые должны применяться на занятиях по математике.
1.
При
разработке гипсового композита исследовалось влияние на плотность ![]() , в сухом состоянии введения
вспученного перлитового песка в количестве от 0 до
, в сухом состоянии введения
вспученного перлитового песка в количестве от 0 до ![]() от массы гипса при формировании изделий из
технологической смеси нормальной густоты (по Суттарду). При гипотезе линейного
снижения
от массы гипса при формировании изделий из
технологической смеси нормальной густоты (по Суттарду). При гипотезе линейного
снижения ![]() в зависимости
от нормализованного фактора
в зависимости
от нормализованного фактора ![]() нужно найти две оценки МНК в модели
нужно найти две оценки МНК в модели ![]() по результатам пяти опытов,
представленных в таблице [4].
по результатам пяти опытов,
представленных в таблице [4].
|
|
-1 |
-0,5 |
0 |
0,5 |
1 |
|
|
1228 |
1136 |
1120 |
1044 |
942 |
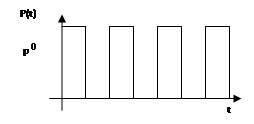
2. Представьте в виде тригонометрического ряда периодические изменения нагрузки с равными периодами действия, показанными на рисунке. Функция нагрузки задана следующим образом:
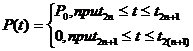
При
этом ![]()
3.
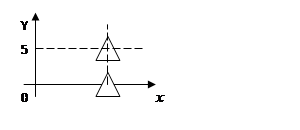
С
помощью подъемного крана извлекают железобетонную надолбу со дна реки глубиной
5 м. Какая работа при этом совершается, если надолба имеет форму правильного
тетраэдра с ребром 1 м (плотность железобетона 2500 кг/![]() , плотность воды 1000 кг/
, плотность воды 1000 кг/![]() )? [6]
)? [6]
Систематическое применение задач прикладного характера при изложении каждой темы дисциплины повышает уровень подготовки обучающихся, а также повышает уровень мотивации изучения предмета, выделяет его перспективу [5]. Об этом свидетельствуют результаты проведенного нами педагогического эксперимента в строительном вузе. Для его осуществления мы построили обучение математике в двух экспериментальных группах посредством решения прикладных задач и проверили уровень их знаний после изучения математики в первом семестре.
Обработку
результатов провели, воспользовавшись средствами статистики: с помощью критерия
χ2 – Пирсона, для которого оказались выполненными все необходимые
допущения. Определили значимость различий по уровню усвоения математических
знаний экспериментальной и контрольной групп. Нулевая гипотеза (![]() ) предполагает равенство вероятностей
уровней подготовки студентов контрольных и экспериментальных групп, при
альтернативной гипотезе (
) предполагает равенство вероятностей
уровней подготовки студентов контрольных и экспериментальных групп, при
альтернативной гипотезе (![]() )
о неравенстве таких вероятностей. В контрольных группах средний балл
принадлежит интервалу 47-67 и согласно критерию Пирсона удовлетворяет закону
нормального распределения. Для проверки выдвинутой нами гипотезы заполнили
необходимые таблицы для расчета выборки полученных баллов у экспериментальных
групп. В данных группах обучалось 100 студентов, и после контрольного теста ими
были получены следующие баллы (табл. 1).
)
о неравенстве таких вероятностей. В контрольных группах средний балл
принадлежит интервалу 47-67 и согласно критерию Пирсона удовлетворяет закону
нормального распределения. Для проверки выдвинутой нами гипотезы заполнили
необходимые таблицы для расчета выборки полученных баллов у экспериментальных
групп. В данных группах обучалось 100 студентов, и после контрольного теста ими
были получены следующие баллы (табл. 1).
Таблица 1
Выборка полученных баллов
|
52 |
72 |
86 |
92 |
61 |
84 |
93 |
85 |
41 |
97 |
|
82 |
53 |
25 |
64 |
76 |
78 |
43 |
78 |
82 |
62 |
|
76 |
84 |
54 |
84 |
75 |
86 |
76 |
83 |
92 |
86 |
|
77 |
34 |
83 |
72 |
66 |
56 |
87 |
62 |
81 |
58 |
|
99 |
73 |
91 |
45 |
73 |
87 |
63 |
76 |
83 |
93 |
|
68 |
85 |
54 |
82 |
95 |
65 |
83 |
95 |
76 |
83 |
|
97 |
74 |
87 |
37 |
88 |
77 |
92 |
68 |
85 |
59 |
|
67 |
91 |
55 |
83 |
45 |
85 |
94 |
87 |
39 |
86 |
|
83 |
95 |
73 |
98 |
93 |
56 |
84 |
61 |
68 |
77 |
|
75 |
45 |
71 |
65 |
95 |
76 |
76 |
86 |
65 |
94 |
Провели
следующие расчеты. ![]() ,
, ![]() .
.
Шаг
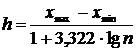 ,
, 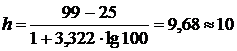 .
.
За
начало первого интервала взяли величину ![]() .
.
Сгруппированный ряд представили в виде таблицы (табл. 2).
Таблица 2
Расчеты эксперимента
|
i |
Интервалы
|
|
ni
|
ui |
niui |
niui2 |
niui3 |
niui4 |
ni(ui+1)4 |
|
1 |
20-30 |
25 |
1 |
-6 |
-6 |
36 |
-216 |
1296 |
625 |
|
2 |
30-40 |
32 |
3 |
-5 |
-15 |
75 |
-375 |
1875 |
768 |
|
3 |
40-50 |
42 |
5 |
-4 |
-20 |
80 |
-320 |
1280 |
405 |
|
4 |
50-60 |
52 |
9 |
-3 |
-27 |
81 |
-243 |
729 |
144 |
|
5 |
60-70 |
62 |
14 |
-2 |
-28 |
56 |
-112 |
224 |
14 |
|
6 |
70-80 |
72 |
21 |
-1 |
-21 |
21 |
-21 |
21 |
0 |
|
7 |
80-90 |
82 |
29 |
0 |
0 |
0 |
0 |
0 |
29 |
|
8 |
90-100 |
92 |
18 |
1 |
18 |
18 |
18 |
18 |
288 |
|
|
|
|
100 |
|
-99 |
367 |
-1269 |
5443 |
2273 |
![]() - условная варианта,
- условная варианта, 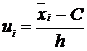 ,
, ![]() -
ложный нуль.
-
ложный нуль.
Для контроля вычислений пользовались тождеством:
![]() .
.
Контроль: ![]() ,
,
![]()
![]()
![]() .
.
Совпадение контрольных сумм свидетельствует о правильности вычислений.
Вычислили условные моменты первого и второго порядка, выборочную среднюю:
![]() ;
; ![]() ;
;
![]() .
.
Нашли выборочную дисперсию, выборочное среднее квадратическое отклонение:
![]() ,
,
![]() =
=![]() .
.
Чтобы
использовать ![]() (хи-квадрат) - критерий Пирсона, взяли
выборочную среднюю
(хи-квадрат) - критерий Пирсона, взяли
выборочную среднюю ![]() , выборочное среднее
квадратическое отклонение
, выборочное среднее
квадратическое отклонение ![]() .
.
При
уровне значимости ![]() (надежность
(надежность ![]() ) проверили гипотезу о том, что случайная
величина
) проверили гипотезу о том, что случайная
величина ![]() , заданная нашими баллами, также распределена
по нормальному закону. Если
, заданная нашими баллами, также распределена
по нормальному закону. Если ![]() , то нет оснований
отвергнуть гипотезу о нормальном распределении генеральной совокупности, в
обратном случае наша гипотеза (
, то нет оснований
отвергнуть гипотезу о нормальном распределении генеральной совокупности, в
обратном случае наша гипотеза (![]() ) отвергается [1].
) отвергается [1].
Чтобы
найти ![]() , составили таблицу (табл. 3).
, составили таблицу (табл. 3).
Прономеровали
Х, т.е. перешли к случайной
величине ![]() , и вычислили вероятность попадания Х в интервал
, и вычислили вероятность попадания Х в интервал ![]() :
:
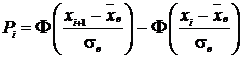 .
.
Затем
вычислили теоретические частоты: ![]() , где n – объем выборки (сумма всех частот), n = 100, чтобы найти наблюдаемое значение
критерия:
, где n – объем выборки (сумма всех частот), n = 100, чтобы найти наблюдаемое значение
критерия: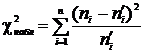 .
.
Таблица 3
Вычисление
![]() Пирсона
Пирсона
|
i |
Интервалы
|
Эмпири-ческая частота
|
Вероятность
|
Теорети-ческие частоты
|
|
|
|
|
1 |
20-30 |
1 |
9 |
0,04326 |
4,326 |
21,84628 |
5,049994 |
|
2 |
30-40 |
3 |
|||||
|
3 |
40-50 |
5 |
|||||
|
4 |
50-60 |
9 |
0,0921 |
9,21 |
46,1041 |
5,005874 |
|
|
5 |
60-70 |
14 |
0,1794 |
17,94 |
15,5236 |
0,865307 |
|
|
6 |
70-80 |
21 |
0,2327 |
23,27 |
5,1529 |
0,22144 |
|
|
7 |
80-90 |
29 |
0,2195 |
21,95 |
49,7025 |
2,264351 |
|
|
8 |
90-100 |
18 |
0,1426 |
14,26 |
13,9876 |
0,980898 |
|
|
|
|
100 |
0,90056 |
|
|
14,38786 |
|
По таблице критических точек
распределения ![]() (уровень значимости
(уровень значимости ![]() и число степеней свободы
и число степеней свободы ![]() ) нашли
) нашли![]() .
.
В нашем случае ![]() ,
,
![]() и
и ![]() .
.
Поскольку эмпирическое значение χ2 больше его критического значения (14,38786>7,8), полученные результаты дали достаточное основание для отклонения нулевой гипотезы. Другими словами, уровень усвоения знаний повысился у студентов экспериментальной группы за счет использования задач прикладного характера в более существенной мере, чем у студентов контрольной группы.
Преподавателями экспериментальных групп было отмечено, что предложенная методика использования прикладных задач при изучении каждой темы курса математики у будущих строителей позволила получить подавляющему большинству студентов более гибкую и вариативную систему знаний по математике, что в дальнейшем должно способствовать более эффективному изучению смежных и специальных дисциплин. Таким образом, проведенный нами эксперимент доказал целесообразность использования прикладных задач на занятиях по математике.
Рецензенты:Усманов В.В., д.п.н., профессор, первый проректор, проректор по научной работе, ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза;
Гарькина И.А., д.т.н., профессор, профессор кафедры математики и математического моделирования, ФГБОУ ВПО «Пензенский государственный университет архитектуры и строительства», г. Пенза.
Библиографическая ссылка
Титова Е.И., Ячинова С.Н., Киселев А.А. ЭКСПЕРИМЕНТАЛЬНАЯ ОЦЕНКА ПРИМЕНЕНИЯ ЗАДАЧ ПРИКЛАДНОГО ХАРАКТЕРА НА ЗАНЯТИЯХ ПО МАТЕМАТИКЕ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18660 (дата обращения: 13.02.2026).