Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Господариков А.П. 1 Колтон Г.А. 1 Булдаков Е.Л. 1

---

1 Национальный минерально-сырьевой университет «Горный»

Из общих уравнений механики сплошной среды, теории тонких оболочек и уравнений гидравлики составлена математическая модель нефтепровода, находящегося в скальном грунте для дальнейшего расчета скоростей смещений стенки трубы при воздействии сейсмовзрывных волн. Задача сформулирована в плоской постановке, для прямого интегрирования исходной системы уравнений выбран метод конечных разностей. На контакте массива и трубопровода рассмотрены краевые условия вида: «проскальзывание» и «жесткое защемление». Математическая модель реализована в вычислительной программе на алгоритмическом языке Фортран 90. В работе приводится сравнительный анализ результатов численного и натурного экспериментов – сравниваются значения компонент скоростей смещений массива на поверхности. Получены значения компонент скоростей смещений стенки трубопровода при воздействии сейсмовзрывной нагрузки.

Статья в формате PDF

592 KB

математическая модель

Нефтепровод

взрывная волна

скальный грунт

1. Боровиков В.А., Ванягин И.Ф., Менжулин М.Г., Цирель C.B. Волны напряжений в обводнённом трещиноватом массиве. – Л.: Изд. ЛГИ, 1989. – 85 с.

2. Валландер С.В. Лекции по гидроаэромеханике. – Л.: Изд-во Ленингр. ун-та, 1978. – 296 С.

3. Годунов С.К., Рябенький В.С. Разностные схемы. – М.: Наука, 1973. – 400 с.

4. Господариков А.П., Колтон Г.А., Булдаков Е.Л. Об одном подходе к математическому моделированию воздействия взрывных волн на подземный нефтепровод // Записки Горного института. – 2014. – Т. 210. – С. 37-42.

5. Новожилов В.В., Черных К.Ф., Михайловский Е.И. Линейная теория тонких оболочек. – Л.: Политехника, 1991. – 656 с.

6. Brian D. Hahn, Edward Arnold. Fortran 90 for Scientists and Engineers – University of Cape Town, 1994. – 198 p.

Строительство траншей для прокладки нефтепроводов тесно связано с проведением большого объема земляных работ. Особую трудность представляет разработка скальных грунтов, для рыхления которых вполне обосновано применение энергии взрыва.

Наращивание объемов перекачки нефти, связанное со строительством второй нитки нефтепровода вблизи действующего нефтепровода, приводит к необходимости оценки сейсмического воздействия взрыва (при разработке траншеи в скальном грунте) на эксплуатируемый нефтепровод.

Для исследования воздействия взрыва на действующий подземный нефтепровод требуется провести большое количество натурных испытаний, что экономически и технически не всегда возможно. Поэтому для изучения сейсмического воздействия взрыва на нефтепровод в работе приводятся результаты численного моделирования взаимодействия продольной волны, распространяющейся в упругой среде с оболочкой, заполненной жидкой средой. Последние получены на основе работы [4], где напряженно-деформированное состояние массива скальных пород при динамическом нагружении описывается системой дифференциальных уравнений в частных производных первого порядка, объединяющую в себе как уравнения движения, так и продифференцированный по времени закон Гука [3]:

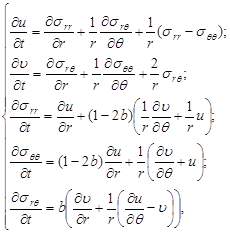(1)

где – радиальная и тангенциальная компоненты вектора скоростей; – компоненты тензора напряжений; – коэффициент Пуассона.

При математическом моделировании нефтепровода в работе используются основные положения теории тонких оболочек, в которой напряженное состояние трубопровода описывается известными уравнениями Новожилова В.В. с учетом продифференцированного закона Гука [5]:

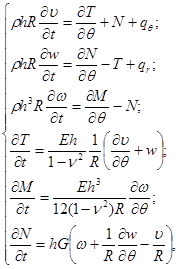(2)

где – радиальная и тангенциальная компоненты вектора скоростей; – скорость сдвига; h – толщина оболочки; – касательное и нормальное усилия; М – изгибающий момент; ; – модуль Юнга; – коэффициент Пуассона; – плотность материала трубы; , – компоненты вектора поверхностной нагрузки; R – радиус срединной поверхности оболочки.

Движение жидкости внутри оболочки описывается известными линеаризованными уравнениями Эйлера [2]:

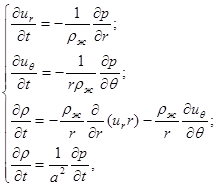(3)

где – давление; и – текущая и начальная плотности; – компоненты вектора скоростей; а – скорость распространения продольной волны в жидкости.

В качестве начальных условий нагружения массива скальных пород используется следующая зависимость [1]:

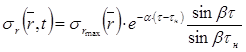, (4)

где – максимальное значение радиальной составляющей волны напряжений; – акустическая жесткость породы; – относительное расстояние; r – расстояние от оси заряда до исследуемой области сейсмического воздействия; – радиус заряда; – коэффициент, характеризующий крутизну нарастания и спада амплитуды напряжения во времени; – текущее время с момента прихода волны на расстояние r; – время нарастания амплитуды напряжений до максимума; – коэффициент; характеризующий продолжительность положительной фазы волны напряжений.

Таким образом, приведенная замкнутая система дифференциальных уравнений (1), (2) и (3) с учетом краевых условий (4), представляет собой математическую модель совместного движения грунта, трубопровода и заполняющей его жидкости в условиях внешнего динамического нагружения. Для сформулированной краевой задачи на основе численного алгоритма [4], базирующегося на методе конечных разностей, разработана вычислительная программа на алгоритмическом языке Фортран-90 [6].

Для исследования скоростей смещения стенки трубопровода проведены численные эксперименты. Исследован нефтепровод (модуль Юнга равен 21·1010 Па; коэффициент Пуассона – 0,28; плотность материала трубы – 7874 кг/м3) диаметром 820 мм с толщиной стенки 12 мм, по которому транспортируется нефть плотностью 850 кг/м3; давление перекачиваемой нефти в рассматриваемом сечении нефтепровода 7 МПа. На расстоянии 15 м от трубопровода в граните (модуль Юнга равен 5,79·1010 Па; коэффициент Пуассона – 0,3; плотность скального грунта – 2700 кг/м3) произведены взрывные работы с зарядами взрывчатого вещества по 28 кг в каждой ступени. Результаты численного эксперимента представлены на рисунках 2–5. На рисунке 1 схематично показано расположение исследуемых точек 1–3 трубопровода и 4–7 грунтового массива (стрелками указано направление набегающей сейсмовзрывной волны). Для исключения фактора отражения волн от границ массива грунта последний моделируется бесконечной областью. Время отсчитывается от момента контакта сейсмовзрывной волны с трубопроводом.

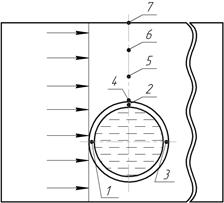
Рис.1. Схема воздействия сейсмовзрывной волны с указанием исследуемых точек 1–7

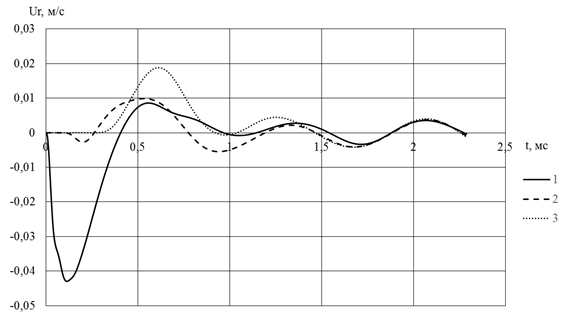
Риc. 2. Зависимости радиальных компонент векторов скоростей от времени

(1, 2 и 3 – исследуемые точки трубопровода)

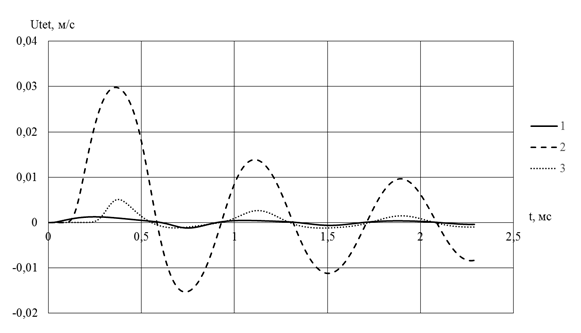
Рис. 3. Зависимости тангенциальных компонент векторов скоростей от времени

(1, 2 и 3 – исследуемые точки трубопровода)

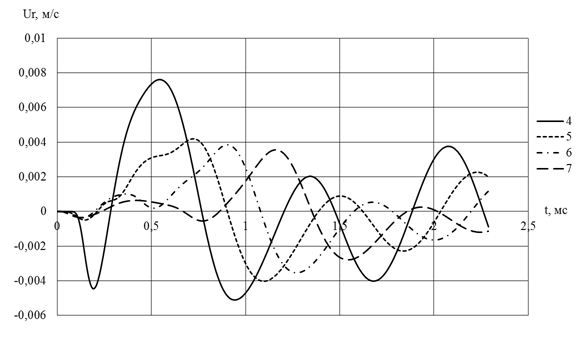
Рис. 4. Зависимости радиальных напряжений в скальном массиве от времени

(4, 5, 6 и 7 – исследуемые точки массива)

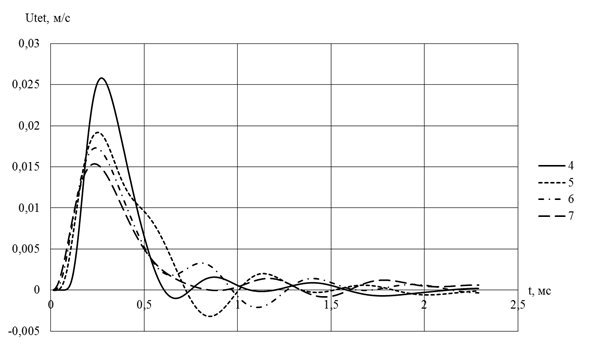
Рис. 5. Зависимости тангенциальных напряжений в скальном массиве от времени

(4, 5, 6 и 7 – исследуемые точки массива)

Результаты численных экспериментов сравнивались с результатами замеров компонент скоростей смещения точек массива при натурных испытаниях. Двухкомпонентный датчик был установлен на поверхности грунта, взрыв производился на расстоянии 15 метров от датчика. Производилось короткозамедленное взрывание 32 ступеней со средней массой взрывчатого вещества в каждой ступени 28 кг. Высота засыпки над трубопроводом равна 1,5 м. Результаты натурных замеров представлены на рисунках 6 и 7.

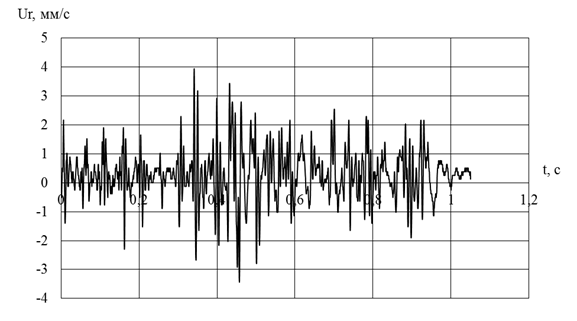
Рис. 6. Результаты замера радиальной компоненты скорости смещения грунта

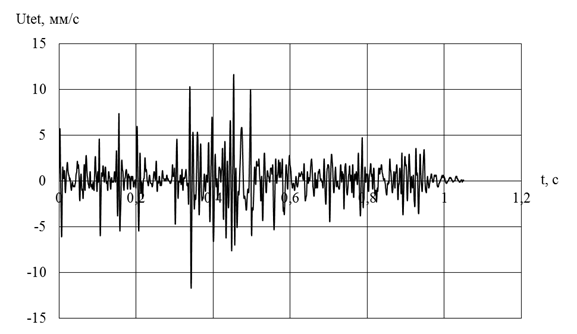
Рис. 7. Результаты замера тангенциальной компоненты скорости смещения грунта

Максимальные значения скоростей смещений грунта на эпюрах (рис. 4 и 5) для зависимости №7 (на поверхности грунта) составляют 3,5 мм/с и 15 мм/с, а полученные натурные значения скоростей смещения грунта (рис. 6 и 7) в экстремальных точках достигают 4 мм/с для радиальной компоненты и 11 мм/с для тангенциальной компоненты вектора скоростей.

Таким образом, результаты численного эксперимента вполне сопоставимы с результатами натурных испытаний. Полученные максимальные значения скоростей смещений стенки трубопровода (42 мм/с и 30 мм/с (рис. 2 и 3)) не превышают нормативного значения, равного 100 мм/с. Разработанные алгоритм и вычислительная программа, реализующие математическую модель взаимодействия сейсмовзрывных волн с подземным нефтепроводом, позволяют исследовать динамические процессы, протекающие в стенке трубы при различных параметрах ведения буровзрывных работ.

Рецензенты:

Коршунов Г.И., д.т.н., профессор, заведующий кафедрой безопасности производств Национального минерально-сырьевого университета «Горный», г. Санкт-Петербург;

Парамонов Г.П., д.т.н., профессор, заведующий кафедрой взрывного дела Национального минерально-сырьевого университета «Горный», г. Санкт-Петербург.

Библиографическая ссылка