Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Оценка качества эргатической системы «оператор – имитатор объекта» с позиций  когнитивного моделирования сводится к оценке управляющих воздействий в системе «оператор – реальный объект» [4, 6]. Правда, на сегодня, за исключением режимов компенсирующего и преследующего отслеживания, нет четкого определения управляющих воздействий. Так, при компенсирующем отслеживании оператор следит только за рассогласованием между входом и выходом, которое стремится уменьшить до нуля. При преследующем отслеживании оператору независимо предъявляются и входной и выходной сигналы, которые он стремится совместить. Определение управляющих воздействий целесообразно производить по данным нормальной эксплуатации. В этом случае  возможно осуществлять формализованную оценку привития навыков управления, качества управления и качества  имитатора. Важным является и возможность построения для наиболее распространенного режима стабилизации программного движения структурной схемы эргатической системы [8]. При квазилинейной модели схема приводится к одноконтурной системе управления. При этом параметрическую идентификацию системы по данным нормальной эксплуатации можно производить с использованием  итерационной процедуры (с последовательным уточнением параметров объекта и оператора).

 При разработке обучающих комплексов возникает необходимость определения некоторых объективных показателей для последующего их сопоставления с субъективной оценкой оператором качества объекта в процессе  нормального функционирования. В [6] в качестве одного из перспективных методов предлагается решение  этого вопроса на основе классификации уравнений движения объекта (для продольного движения объекта в предположении линейности управляющих воздействий относительно фазовых координат). Обобщение результатов на случай более сложных законов управления не встречает больших затруднений [1…3].

Одним из актуальных вопросов при разработке тренажеров по подготовке операторов мобильных транспортных систем является оптимизация параметров матрицы управления, соответствующей оптимальным управляющим воздействиям оператора. Ограничимся случаем, когда уравнения движения эргатической системы имеют вид:

.

(1)

Здесь:

,

-

векторы фазовых координат и управляющих воздействий.

Непосредственно из соображений энергетического характера следует:

.

(2)

При  (отсутствие управления) эргатическая система  полностью определяется основной матрицей системы  и матрицей управления . Парой матриц   и  полностью характеризуется техническая часть системы (включая возможности идеальной эксплуатации с идеальным оператором в управляемой эргатической системе). В общем случае, естественно, следует учитывать и случайные возмущения , внешние по отношению к ее технической части (обычно известны лишь статистические характеристики). На начальном этапе они могут не учитываться.

  В дискретной форме уравнения движения (1) имеют вид:

,

где

,

.

Запаздывание  принималось, исходя из интервала дискретизации :

.

В этом случае оценка матрицы  определяется  по синхронным измерениям в процессе нормальной эксплуатации фазовых координат и управляющих воздействий (возможна их  аппроксимация [5,8]).

Справедливо соотношение:

,

где

,

.

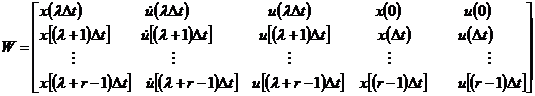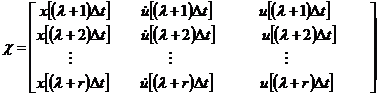Как видим, при заданных матрицах  и  задача сводится к нахождению матриц , которыми и определяются оптимальные управляющие воздействия человека-оператора.

Для линейных, стационарных объектов управления оценка качества может производиться по корневым годографам. В частности, можно воспользоваться функционалом:

;

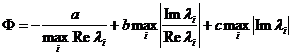- собственные числа матрицы  (приняты: ,).

Очевиден физический смысл каждого из слагаемых функционала:

1) длительность переходных процессов в системе определяется первым слагаемым ;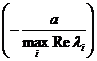

2) второе слагаемое 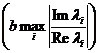 характеризует относительную колебательность переходных режимов;

3) абсолютную колебательность переходных процессов определяет третье слагаемое .

Здесь  - неотрицательные весовые константы, которые могут определяться по вычисленным на основе экспериментальных данных коэффициентам корреляции между  и каждым из слагаемых (частных критериев).

Для линейной и стационарной системы:

.

Энергия управляющих воздействий для реальных систем ограниченная; так что норма  . При этом норма . Справедливо:

(следует из свойств нормы матриц); очевидно ограничение на норму матрицы :

.

Из физического смысла функционала следует, что система тем лучше, чем меньше . Оптимальная обратная связь в системе, определяемой уравнением (1), удовлетворяет условию:

.

            При заданных  и  значение функционала фактически определяется элементами матриц , т. е. . Оптимальные значения наиболее просто определятся методом наискорейшего спуска в сочетании с методом штрафных функций (антиградиентное направление функции   является направлением наискорейшего спуска). Часто для определения оценки вектора-градиента можно воспользоваться методами дробно-факторного эксперимента. Однако следует помнить, что метод наискорейшего спуска применим лишь для безусловной минимизации (затруднения при минимизации на границе рассматриваемой области D изменения параметров матриц ). В силу (2) область D не совпадает со всем пространством параметров. Поэтому задачу условной минимизации   приходится сводить к эквивалентной задаче безусловной минимизации (например, используя метод штрафных функций). Суть метода состоит в построении по  новой функции, достаточно быстро растущей вне области D и совпадающей с  на этой области. Естественно, при конструировании вспомогательной функции необходимо исключить возможность переполнения при расчетах.

            Непосредственно из приведенного с очевидностью следует, что стиль и классность управления определяются разбросом в процессе нормальной эксплуатации значений  относительно  , соответствующей системе (1)  с .

            Приведенные подходы к оптимизации управления в эргатической системе прошли положительную апробацию при имитационном моделировании транспортных тренажеров различного назначения [7] и рекомендуются к использованию при анализе и синтезе аналогичных сложных систем.

Рецензенты:

Родионов Ю.В., д.т.н., профессор, декан автомобильно-дорожного института ПГУАС, заведующий кафедрой «Эксплуатация автомобильного транспорта», г. Пенза;

Кошев А.Н., д.х.н., профессор, профессор кафедры «Информационно-вычислительные системы» Пензенского государственного университета архитектуры и строительства, г. Пенза.