В статье выполнен синтез параллельного алгоритма построения декартова дерева с применением максимально параллельной модификации сортировки подсчетом на основе матриц сравнений. При параллельном построении поддеревьев используются взаимно независимые сравнения элементов по типу отдельных строк таких матриц, что аналогично операциям сортировки Хоара в параллельной форме. Для множества ![]() пар элементов
пар элементов ![]() временная сложность построения декартова дерева оценивается из соотношения
временная сложность построения декартова дерева оценивается из соотношения ![]() , где число процессоров
, где число процессоров ![]() . Оценка получена на модели неветвящихся параллельных программ без учета операций обмена. В статье приводятся примеры использования параллельной сортировки, а также пошаговой интерпретации работы параллельного алгоритма построения декартова дерева в процессе определения корней и ветвей поддеревьев. Предложенный алгоритм распараллеливается на уровне алгоритмических и разрядных операций.
. Оценка получена на модели неветвящихся параллельных программ без учета операций обмена. В статье приводятся примеры использования параллельной сортировки, а также пошаговой интерпретации работы параллельного алгоритма построения декартова дерева в процессе определения корней и ветвей поддеревьев. Предложенный алгоритм распараллеливается на уровне алгоритмических и разрядных операций.
Постановка вопроса. Ускоряющаяся компьютеризация всех областей деятельности и информационных процессов, значительный рост объемов обрабатываемой информации приводит к трудностям при последовательном выполнении информационного поиска на основе традиционных алгоритмов [1, 3]. Древовидные структуры характеризуются эффективностью представления динамических данных для быстрого поиска информации. С целью дальнейшего увеличения эффективности целесообразна разработка и исследование алгоритмов параллельного построения древовидных структур данных. В таком аспекте ставится задача синтеза и оценки временной сложности параллельного алгоритма построения декартова дерева. Параллельные алгоритмы рассматриваются на модели неветвящихся параллельных программ, согласно которой временная сложность ![]() алгоритма (кратко – время выполнения) измеряется количеством последовательных шагов без учета обмена,
алгоритма (кратко – время выполнения) измеряется количеством последовательных шагов без учета обмена, ![]() – число процессоров [9].
– число процессоров [9].
Сортировка подсчетом. На этапе построения декартова дерева ко всем компонентам будет применяться максимально параллельная сортировка подсчетом по матрице сравнений [5]. Модификация известного алгоритма заключается в следующем. Для одномерного массива ![]() сортируемых элементов составляется матрица сравнений, элемент
сортируемых элементов составляется матрица сравнений, элемент ![]() которой определяется из соотношений:
которой определяется из соотношений:
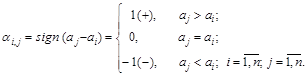
Входной элемент с номером ![]() получает номер
получает номер ![]() в отсортированном массиве по правилу: в
в отсортированном массиве по правилу: в ![]() -м столбце матрицы подсчитывается количество нулей и плюсов сверху вниз до главной диагонали включительно и складывается с количеством только плюсов ниже диагонали в этом же столбце. Суммарное количество составит значение выходного номера
-м столбце матрицы подсчитывается количество нулей и плюсов сверху вниз до главной диагонали включительно и складывается с количеством только плюсов ниже диагонали в этом же столбце. Суммарное количество составит значение выходного номера ![]() . Пусть, например, требуется отсортировать по неубыванию массив
. Пусть, например, требуется отсортировать по неубыванию массив ![]() .
.
Матрица сравнений примет вид:
|
|
|
|
|
|
|
|
|
|
|
|
1 |
–1 |
0 |
3 |
–3 |
5 |
|
|
1 |
0 |
– |
– |
+ |
– |
+ |
|
|
–1 |
+ |
0 |
+ |
+ |
– |
+ |
|
|
0 |
+ |
– |
0 |
+ |
– |
+ |
|
|
3 |
– |
– |
– |
+ |
– |
+ |
|
|
–3 |
+ |
+ |
+ |
0 |
0 |
+ |
|
|
5 |
– |
– |
– |
– |
– |
0 |
Согласно правилу вставки получится: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Отсортированный массив примет вид:
. Отсортированный массив примет вид: ![]() . Процедура сортировки в консольном приложении Delphi [3, 5] при соответственном задании типа элементов и их индексов запишется в виде:
. Процедура сортировки в консольном приложении Delphi [3, 5] при соответственном задании типа элементов и их индексов запишется в виде:
procedure sort (var n: integer; var a,c: vekt00; var e: vekt);
var i,j,k: integer;
begin
for j:= 1 to n do
begin
k:= 0;
for i:= 1 to j do
if a[j] >= a[i] then k:= k+1;
for i := j+1 to n do
if a[j] > a[i] then k := k+1;
c[k] := a[j]; e[k] := j;
end;
end;
Сортировка сохраняет порядок равных элементов, операторы c[k]:=a[j]; e[k]:=j; в явном виде задают взаимно однозначное соответствие входных и выходных индексов сортируемых элементов. Сортировка обладает максимальным параллелизмом: все сравнения в матрице взаимно независимы и выполнимы параллельно за время ![]() [5].
[5].
Описание метода. Декартово дерево – это структура данных, хранящая в узлах пары элементов ![]() в виде двоичного дерева таким образом, что она является двоичным деревом по
в виде двоичного дерева таким образом, что она является двоичным деревом по ![]() и двоичной пирамидой по
и двоичной пирамидой по ![]() [1]. Двоичное дерево – это структура данных, для которой у левого потомка произвольной вершины значение элемента
[1]. Двоичное дерево – это структура данных, для которой у левого потомка произвольной вершины значение элемента ![]() меньше либо равно значения
меньше либо равно значения ![]() его вершины, а у правого потомка произвольной вершины значение
его вершины, а у правого потомка произвольной вершины значение ![]() строго больше, чем значение
строго больше, чем значение ![]() его вершины. Двоичная пирамида – двоичное дерево, в каждой вершине которой хранится ключ, и для каждой вершины дерева с ключом
его вершины. Двоичная пирамида – двоичное дерево, в каждой вершине которой хранится ключ, и для каждой вершины дерева с ключом ![]() у всех непосредственных потомков ключ не больше значения
у всех непосредственных потомков ключ не больше значения ![]() предка. Пусть задано некоторое множество пар элементов
предка. Пусть задано некоторое множество пар элементов ![]() . Корнем декартова дерева является пара элементов, которая имеет максимальный
. Корнем декартова дерева является пара элементов, которая имеет максимальный ![]() (по условию двоичной пирамиды). Пусть
(по условию двоичной пирамиды). Пусть ![]() – пара с максимальным
– пара с максимальным ![]() . Тогда все пары с меньшими
. Тогда все пары с меньшими ![]() будут в левом поддереве, остальные – в правом поддереве. Каждое из поддеревьев строится аналогично. На рис. 1 изображен пример декартова дерева для массива пар чисел:
будут в левом поддереве, остальные – в правом поддереве. Каждое из поддеревьев строится аналогично. На рис. 1 изображен пример декартова дерева для массива пар чисел:
(1; 4), (1; 12), (4; 13), (9; 14), (4; 7), (6; 8), (7; 6), (12; 5), (13; 11), (14; 12), (18; 0). (1)
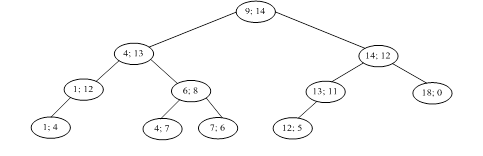
Рис. 1. Пример декартова дерева
Построение декартова дерева с применением представленной максимально-параллельной сортировки (ниже МП-сортировки) выполняется следующим образом. Ко всем компонентам ![]() – элементов данного множества применяется МП-сортировка по неубыванию. При этом пары уже отсортированных по
– элементов данного множества применяется МП-сортировка по неубыванию. При этом пары уже отсортированных по ![]() элементов
элементов ![]() располагаются с сохранением входного индекса без изменения единичной оценки времени. Наибольший среди
располагаются с сохранением входного индекса без изменения единичной оценки времени. Наибольший среди ![]() элемент окажется в правом конце отсортированного массива вместе с входным индексом пары
элемент окажется в правом конце отсортированного массива вместе с входным индексом пары ![]() . Пусть эта пара обозначена
. Пусть эта пара обозначена ![]() , а ее входной индекс –
, а ее входной индекс – ![]() ,
, ![]() , таким образом, определен корень декартова дерева
, таким образом, определен корень декартова дерева ![]() . Далее, без изменения его местоположения во входном массиве, которое идентифицируется по индексу
. Далее, без изменения его местоположения во входном массиве, которое идентифицируется по индексу ![]() , этот элемент объявляется серединным в данном входном массиве. Относительно середины выполняется упорядочение по
, этот элемент объявляется серединным в данном входном массиве. Относительно середины выполняется упорядочение по ![]() : все элементы в левой части массива, которые меньше
: все элементы в левой части массива, которые меньше ![]() из
из ![]() , остаются в левом подмассиве с сохранением исходного взаимного порядка; все элементы в левой части массива, которые больше
, остаются в левом подмассиве с сохранением исходного взаимного порядка; все элементы в левой части массива, которые больше ![]() из
из ![]() , переносятся из левой части в правый подмассив, также с сохранением исходного взаимного порядка. Все элементы правой части массива, которые больше
, переносятся из левой части в правый подмассив, также с сохранением исходного взаимного порядка. Все элементы правой части массива, которые больше ![]() из
из ![]() , остаются в правом подмассиве с сохранением исходного взаимного порядка; все элементы правой части массива, которые меньше
, остаются в правом подмассиве с сохранением исходного взаимного порядка; все элементы правой части массива, которые меньше ![]() из
из ![]() , переносятся из правой части в левый подмассив, также с сохранением исходного взаимного порядка.
, переносятся из правой части в левый подмассив, также с сохранением исходного взаимного порядка.
Излагаемый ниже способ упорядочения относительно середины аналогичен тому, который применяется для параллельного варианта сортировки Хоара [4].
Для примера (1) середина – пара ![]() ,
, ![]() . Упорядочение относительно
. Упорядочение относительно ![]() выполняется параллельно по всем элементам по схеме МП-сортировки в одной строке:
выполняется параллельно по всем элементам по схеме МП-сортировки в одной строке:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
4 |
9 |
4 |
6 |
7 |
12 |
13 |
14 |
18 |
|
|
9 |
– |
– |
– |
0 |
– |
– |
– |
+ |
+ |
+ |
+ |
Все элементы со знаком сравнения "–" из правого подмассива с сохранением индексов переносятся в левый подмассив. В результате получится:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
4 |
4 |
6 |
7 |
9 |
12 |
13 |
14 |
18 |
|
|
9 |
– |
– |
– |
– |
– |
– |
0 |
+ |
+ |
+ |
+ |
Для левого подмассива элементы декартова дерева расположатся в виде:
|
|
|
|
|
|
|
|
(1; 4) |
(1;12) |
(4; 13) |
(4; 7) |
(6; 8) |
(7; 6) |
В сформированном таким способом левом подмассиве повторяется МП-сортировка по ![]() . В результате определяется корень поддерева в этом подмассиве: (4; 13) с исходным индексом
. В результате определяется корень поддерева в этом подмассиве: (4; 13) с исходным индексом ![]() . Относительно его положения в подмассиве выполняется упорядочение по изложенной схеме по
. Относительно его положения в подмассиве выполняется упорядочение по изложенной схеме по ![]() :
:
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
4 |
4 |
6 |
7 |
|
|
4 |
– |
– |
0 |
0 |
+ |
+ |
В результате определились элементы нового поддерева искомого декартова дерева с корнем (4; 13):
|
|
|
|
|
|
|
|
(1; 4) |
(1;12) |
(4; 13) |
(4; 7) |
(6; 8) |
(7; 6) |
Сравнение с серединным элементом выполняется параллельно по всем элементам исходного подмассива аналогично одной строке МП-сортировки за единичное время на процессорах, число которых равно числу ![]() элементов подмассива. Число процессоров для определения корня поддерева равно
элементов подмассива. Число процессоров для определения корня поддерева равно ![]() .
.
Параллельно с левым подмассивом исходного массива аналогично обрабатывается правый подмассив:
|
|
|
|
|
|
(12; 5) |
(13; 11) |
(14; 12) |
(18; 0) |
Повторяется МП-сортировка по ![]() : в результате определяется корень поддерева: (14; 12) с исходным индексом
: в результате определяется корень поддерева: (14; 12) с исходным индексом ![]() . Относительно его исходного положения в данном правом подмассиве выполняется упорядочение по изложенной схеме относительно
. Относительно его исходного положения в данном правом подмассиве выполняется упорядочение по изложенной схеме относительно ![]() :
:
|
|
|
|
|
|
|
|
|
|
12 |
13 |
14 |
18 |
|
|
14 |
– |
– |
0 |
+ |
Тем самым, оказалось, что окончательно сформировано поддерево правого подмассива:
|
|
|
|
|
|
(12; 5) |
(13; 11) |
(14; 12) |
(18; 0) |
На этом завершено полное построение декартова дерева, оно совпадает с деревом, изображенным на рис. 1.
В общем случае описанные действия параллельно повторяются отдельно в каждом подмассиве, при этом наибольший среди ![]() элемент левого подмассива окажется левым потомком корня декартова дерева
элемент левого подмассива окажется левым потомком корня декартова дерева ![]() , наибольший среди
, наибольший среди ![]() элемент правого подмассива окажется правым его потомком.
элемент правого подмассива окажется правым его потомком.
Действия воспроизводятся в каждом новом подмассиве, образуемом потомком как корнем поддерева, причем параллельно по всем подмассивам, соответственным корням текущего уровня.
Шаги описанного параллельного алгоритма продолжаются до полного построения декартова дерева, их количество, очевидно, не превосходит ![]() . Число процессоров в каждом поддереве для МП-сортировки по уровням корней располагается в последовательность:
. Число процессоров в каждом поддереве для МП-сортировки по уровням корней располагается в последовательность:
![]() (2)
(2)
В (2) нечетные индексы соответствуют поддеревьям левых подмассивов, четные – правых. С учетом ![]() получится, что
получится, что
![]() .
.
В общем случае, соответственно уровню корней поддеревьев с номером ![]() ,
, ![]() , количество сортируемых по всем подмассивам элементов удовлетворяет равенству
, количество сортируемых по всем подмассивам элементов удовлетворяет равенству ![]() . Отсюда количество процессоров при параллельном по всем
. Отсюда количество процессоров при параллельном по всем ![]() выполнении МП-сортировки каждого подмассива из
выполнении МП-сортировки каждого подмассива из ![]() элементов на уровне с номером
элементов на уровне с номером ![]() удовлетворяет соотношениям:
удовлетворяет соотношениям:
![]() ,
,
поэтому
![]() .
.
Таким образом, с учетом единичного времени каждого последовательного шага и числа шагов ![]() получается оценка временной сложности предложенного алгоритма:
получается оценка временной сложности предложенного алгоритма:
![]() . (3)
. (3)
Из изложенного вытекает
Теорема 1. Построение декартова дерева может быть выполнено с помощью детерминированного параллельного алгоритма за логарифмическое число шагов с временной сложностью (3), где ![]() – число элементов входного множества пар
– число элементов входного множества пар ![]() .
.
Очевидной является возможность перемещения входных индексов пар ![]() по уровням и подмассивам в соответствии шагам изложенного построения декартова дерева, что дает возможность адресоваться от элементов окончательно построенного декартова дерева непосредственно к элементам входного массива и обратно.
по уровням и подмассивам в соответствии шагам изложенного построения декартова дерева, что дает возможность адресоваться от элементов окончательно построенного декартова дерева непосредственно к элементам входного массива и обратно.
Замечание 1. В [6-8] рассматривается построение декартова дерева с учетом поразрядно-параллельных сравнений элементов без вычисления переноса на основе аналога арифметической обработки [2]. Учитывая время МП-сортировки ![]() и оценку (3), полное построение декартова дерева в максимально параллельной форме на данной основе можно выполнить с временной сложностью
и оценку (3), полное построение декартова дерева в максимально параллельной форме на данной основе можно выполнить с временной сложностью ![]() , где
, где ![]() – число элементов входного множества пар
– число элементов входного множества пар ![]() ,
, ![]() – число разрядов наибольшего по числу символов элемента в наборе,
– число разрядов наибольшего по числу символов элемента в наборе, ![]() – время одного сравнения двух бит.
– время одного сравнения двух бит.
В [6] даны результаты программного эксперимента с последовательным моделированием параллельного алгоритма построения декартова дерева, на выходе которого для произвольного множества пар входных данных всегда получается правильный результат.
Заключение. В статье изложен синтез алгоритма параллельного построения декартова дерева с применением максимально-параллельной сортировки подсчетом и аналога сортировки Хоара в параллельной форме. Временная сложность построения декартова дерева по данному алгоритму имеет оценку вида ![]() . Предложенный алгоритм распараллеливается на уровне алгоритмических и разрядных операций, при этом достигает снижения оценки временной сложности известного аналога [10] построения декартова дерева. Приведены примеры использования сортировки и построения декартова дерева с помощью представленного алгоритма, правильность работы которого подтверждается программными экспериментами [6]. Представленный в статье подход может рассматриваться в качестве основы для увеличения эффективности параллельного построения древовидных структур данных.
. Предложенный алгоритм распараллеливается на уровне алгоритмических и разрядных операций, при этом достигает снижения оценки временной сложности известного аналога [10] построения декартова дерева. Приведены примеры использования сортировки и построения декартова дерева с помощью представленного алгоритма, правильность работы которого подтверждается программными экспериментами [6]. Представленный в статье подход может рассматриваться в качестве основы для увеличения эффективности параллельного построения древовидных структур данных.
Рецензенты:
Веселов Г.Е., д.т.н., директор Института компьютерных технологий и информационной безопасности, Инженерно-технологическая академия Южного федерального университета, г. Таганрог;
Турулин И.И., д.т.н., профессор, профессор кафедры информационных измерительных технологий и систем, Институт нанотехнологий, электроники и приборостроения Южного федерального университета, г. Таганрог.
Библиографическая ссылка
Ромм Я.Е., Чабанюк Д.А. ПАРАЛЛЕЛЬНОЕ ПОСТРОЕНИЕ ДЕКАРТОВА ДЕРЕВА С ЛОГАРИФМИЧЕСКОЙ ОЦЕНКОЙ ВРЕМЕННОЙ СЛОЖНОСТИ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18604 (дата обращения: 12.03.2026).



