Проблема диагностирования состояния здоровья детей привлекает внимание все большего числа исследователей. Эта проблема особенно актуальна в педиатрии, где главной задачей является выявление патологий и хронических заболеваний на ранних этапах развития.
Хорошо известно, что расположенность человека к различным заболеваниям закладывается в основном в первый год жизни, поэтому оценка состояния здоровья именно в этот период является актуальной [1].
Поэтому следует производить оценку состояния здоровья детей в период первого года жизни с целью еще на первоначальных этапах развития организма дать необходимые рекомендации во избежание предпатологических и патологических изменений.
Целью работы является использование статистических методов для оценки состояния здоровья детей.
Характеристика исследуемых данных
Для проведения экспериментальных исследований использовались данные, предоставленные врачами Сибирского государственного медицинского университета (СибГМУ) и лечебно-оздоровительного центра (ЛОЦ) «Здоровая мама – крепкий малыш».
Объектом исследования являются медицинские показатели детей первого года жизни (от рождения до 12 месяцев).
Организм ребенка находится в процессе созревания и взросления, а это происходит непрерывно в определенной закономерной последовательности.
Первый год жизни ребенка принято условно классифицировать на 2 периода: новорожденный (неонатальный) и грудной.
Для постановки диагноза доступны следующие количественные показатели гормонов и веществ, отвечающих за жизнедеятельность организма, измеренные в 1–12 месяцах: тиреотропный гормон (ТТГ), малоновый диальдегид (mda), трийодтиронин (Т3), тироксин (Т4), кортизол (kor), инсулин (ins), витамин Е (е).
Тиреотропный гормон отвечает за нормальную работу щитовидной железы, стимулирует выработку гормонов щитовидной железы. Малоновый диальдегид используется для прогноза и контроля лечения ишемической болезни сердца, а также широкого спектра других заболеваний. Трийодтиронин и тироксин вырабатываются щитовидной железой. Они требуются для нормального внутриутробного развития таких органов и систем ребенка, как нервная система, сердечно-сосудистая система, половая система, опорно-двигательный аппарат и др. Кортизол – гормон стресса, который помогает организму справляться с отрицательными воздействиями внешней среды, стимулирует работу сердца и концентрирует внимание. Инсулин – гормон поджелудочной железы, который уменьшает количество глюкозы в крови, запасая ее в печени. Понижение уровня инсулина влечет развитие заболевания – диабета.
Бесспорно, гормоны оказывают огромное влияние на организм человека, а именно на все биохимические процессы – рост, развитие, размножение, обмен веществ. Для того чтобы организм мог нормально функционировать, необходимо наличие определенного соотношения гормонов в крови.
Обзор методов и моделей решения задачи
Рассматриваемая задача является задачей распознавания образов. Теория статистических решений исторически является наиболее выгодным математическим инструментом для постановки и решения задач распознавания образов. Начала теории статистических решений лежат в основе построений алгоритмов распознавания. Эти алгоритмы, на основе опытных данных некоторого набора параметров, которые характеризуют этот объект, и данных, которые описывают классы анализируемых объектов, обеспечивают определение класса, к которому может быть отнесен конкретный объект. Позднее математический аппарат, применяющийся при решении задач распознавания образов, значительно обогатился за счет использования методов теории информации, алгебры логики математического программирования и некоторых других разделов прикладной математики.
К настоящему времени определенно выделились следующие подходы к решению задач распознавания образов: детерминистский [2], статистический [3], лингвистический [2], алгебраический [4], логический [5, 6].
Логистическая регрессия
Под регрессионным анализом понимают исследование влияния одной или нескольких независимых переменных X1, X2, …, Xp на зависимую переменную Y [7].
Задача регрессионного анализа заключается в построении математической модели, которая позволяет давать оценку значений зависимой переменной по значениям независимых переменных [8].
Основные цели регрессионного анализа:
-
при помощи независимых переменных предсказывать значения зависимой переменной;
-
определять вклад отдельных независимых переменных в изменение зависимой переменной.
Общее уравнение регрессии определяется зависимостью [9]:
![]() (1)
(1)
где F – неизвестная функция, подлежащая определению;
Y – зависимая переменная;
X1,X2, …, Xp – набор независимых переменных;
p – общее количество независимых переменных.
Различают 2 основных вида регрессии [9]:
- линейная;
- нелинейная (гиперболическая, показательная, полиномиальная, степенная, логарифмическая, логистическая).
Для проведения регрессионного анализа в работе используется логистическая регрессия.
Логистическая регрессия – это разновидность множественной регрессии, применяющаяся тогда, когда зависимая переменная может принимать только два взаимоисключающих значения, т.е. является бинарной (дихотомической). Метод бинарной логистической регрессии позволяет изучить, как зависит дихотомическая переменная от независимых переменных, которые могут быть измерены в разных шкалах. Чаще всего при использовании дихотомических переменных, когда речь идёт о некотором событии, которое может наступить или не наступить (0 – событие не произошло, 1 – событие произошло), бинарная логистическая регрессия позволяет рассчитать вероятность наступления события в зависимости от значения независимых переменных. При этом используется следующее уравнение регрессии:
![]() ( 2)
( 2)
где Y – зависимая переменная, принимающая значения 0 или 1;
X1,…,Xp – набор зависимых переменных;
β0, …,βp – логистические регрессионные коэффициенты.
Таким образом, формула (2) описывает вероятность того, что событие наступит, т.е. независимая переменная Y примет значение, равное 1, в зависимости от независимых переменных X1,…,Xp .
Если значение P получится меньше 0,5, то можно считать, что событие не наступит, в противоположном случае можно полагать наступление события.
Зависимость, связывающая вероятность события и величину Y, которая называется логистической кривой, показана на рисунке 1.
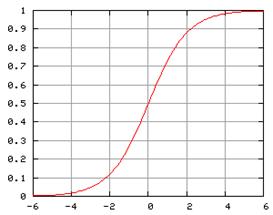
Рис. 1. Логистическая кривая
Из формулы (2) и рисунка 1 можно увидеть, что в этой модели независимо от коэффициентов регрессии β0, …, βp или величин X1,…,Xp, спрогнозированные значения Y всегда будут находиться в диапазоне от 0 до 1.
Для нахождения коэффициентов логистической регрессии используется метод максимального правдоподобия. Суть этого метода заключается в том, что процесс оценки коэффициентов регрессии сводится к максимизации вероятности появления конкретной выборки (при заданных наблюдаемых значениях).
Анализ результатов исследования
Экспериментальные исследования проводились с целью получить результат, отражающий либо наличие заболевания у ребенка, либо его отсутствие, и сравнить этот результат с диагнозом, поставленным врачом.
По результатам обследования 198 детей формируется выборка, которая разделена на 2 класса (диагноза): здоровые (154 детей) и больные (44 ребенка).
Вычисления проводились с использованием статистического пакета SРSS Statistics [10].
С помощью регрессионного анализа было установлено, что только 13 количественных переменных влияют на постановку диагноза: Т41, kor1-3, kor6, ins5-12. Остальные переменные, такие как kor4-12 не вошли в уравнение регрессии.
В таблице 1 представлена классификационная таблица, в которой предсказываемые значения зависимой переменной, посчитанные по уравнению регрессии, сравниваются с фактическими наблюдаемыми значениями.
Таблица 1
Таблица классификации
|
|
Наблюденные |
Предсказанные |
|||
|
Состояние |
Процент правильных |
||||
|
Здоров |
Болен |
||||
|
Шаг 1 |
Состояние |
Здоров |
148 |
6 |
96,1 |
|
Болен |
25 |
19 |
43,2 |
||
|
Общая процентная доля |
|
|
84,3 |
||
Для определения прогнозируемой величины для каждого объекта вычисляется вероятность, на основании которой текущему объекту присваивается одно из двух значений бинарной переменной. В случае если вероятность оказалась менее 0,5, то диагноз – «здоров» (значение переменной «диагноз» равно 0), в противоположном случае – «болен» (значение переменной «диагноз» равно 1). Из таблицы 1 можно увидеть, что для 84,3 % объектов исследования предсказанные результаты оказались верными. Это хороший результат, но процент правильного распознавания больных детей очень мал, что на практике может привести к отрицательным результатам.
В Таблице 2 приводится порядок включения независимых переменных в уравнение регрессии на каждом шаге его построения.
Таблица 2
Переменные в уравнении
|
|
B |
Стандартное отклонение |
Критерий Вальда |
Знач. |
Exp |
|
|
Шаг 1a |
Т41 |
-0,13 |
0,03 |
15,12 |
0 |
0,87 |
|
kor1 |
22,41 |
24,67 |
0,82 |
0,36 |
5,41*109 |
|
|
kor2 |
-55,57 |
61,66 |
0,81 |
0,36 |
0 |
|
|
kor3 |
36,69 |
41,09 |
0,79 |
0,37 |
8,60*1015 |
|
|
kor6 |
-3,51 |
4,10 |
0,73 |
0,39 |
0,03 |
|
|
ins5 |
116,59 |
78,30 |
2,21 |
0,13 |
4,33*1050 |
|
|
ins6 |
-80,53 |
141,27 |
0,32 |
0,56 |
0 |
|
|
ins7 |
-206,24 |
81,78 |
6,37 |
0,01 |
0 |
|
|
ins8 |
39,23 |
80,44 |
0,23 |
0,62 |
1,09*1017 |
|
|
ins9 |
179,46 |
65,78 |
7,44 |
0,01 |
8,68*1077 |
|
|
ins10 |
34,04 |
78,39 |
0,18 |
0,66 |
6,09*1014 |
|
|
ins11 |
-69,56 |
77,06 |
0,81 |
0,36 |
0 |
|
|
ins12 |
-13,53 |
50,07 |
0,07 |
0,78 |
0 |
|
|
Константа |
14,34 |
3,77 |
14,42 |
0 |
1,69*106 |
|
В таблице используются следующие обозначения:
В – коэффициенты регрессионного уравнения;
Стандартное отклонение – мера изменчивости коэффициентов регрессионного уравнения В;
Критерий Вальда – критерий значимости коэффициентов регрессионного уравнения для соответствующего прогностического параметра. Чем выше значение, тем выше значимость.
Ехр – еВ.
С учетом найденных коэффициентов, уравнение регрессии запишется в виде формулы:
![]() (3)
(3)
Для вычисления вероятности того, что ребенок болен, необходимо в уравнение регрессии подставить значения переменных ![]() , соответствующие каждому объекту (состоянию ребенка).
, соответствующие каждому объекту (состоянию ребенка).
Заключение
Логистическая регрессия имеет большое значение и практическое применение в медицине. Метод был апробирован на реальных медицинских данных, предоставленных медицинскими работниками. Качество распознавания, 84,3 % детей был правильно отнесен к соответствующему классу, можно считать приемлемым.
Рецензенты:
Берестнева О.Г., д.т.н., профессор, кафедра Прикладной математики, Национальный исследовательский Томский политехнический университет, Институт кибернетики, г. Томск;
Кривоногова Т.С., д.м.н., профессор, Лечебно-оздоровительный центр «Здоровая мама – крепкий малыш», г. Томск.
Библиографическая ссылка
Черкашина Ю.А. ПРИМЕНЕНИЕ РЕГРЕССИОННОГО АНАЛИЗА В ЗАДАЧЕ ДИАГНОСТИРОВАНИЯ СОСТОЯНИЯ ЗДОРОВЬЯ ДЕТЕЙ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18545 (дата обращения: 12.03.2026).



