Неучет отличия распределения атмосферных и индустриальных помех, являющихся основными видами непреднамеренных помех в метровых (МВ) и декаметровых (ДКМВ) диапазонах волн, используемых при управлении воздушным движением (УВД) с автоматическим зависимым наблюдением (АЗН), от нормального приводит к существенному ухудшению качества его функционирования. В статье предложен сравнительно простой способ моделирования указанных помех при полунатурных испытаниях РЭО.
Известные принципы статистического моделирования негауссовых помех [2] предполагают использование четырехмерного совместного распределения амплитуды и фазы смеси сигнала и помехи, которое, как правило, неизвестно. Это представляет значительные трудности при реализации этих методов на практике.
В данной cтатье статистическое моделирование квазиимпульсных помех типа атмосферных и индустриальных предлагается производить путем формирования реализации импульсной составляющей помехи на основе известных из литературы распределений длительности выбросов помехи Wd(x) и интервалов между ними Wi(х), полученных в рамках аналитической модели квазиимпульсных помех, с последующим заполнением интервалов между выбросами нормальным коррелированным шумом.
В качестве аналитической модели импульсной составляющей квазиимпульсной помехи выбрана логарифмически нормальная модель [1], обеспечивающая хорошее совпадение с экспериментальными данными при описании характеристик выбросов атмосферных и индустриальных помех [6] в ДКМВ и МВ диапазонах и легко согласующаяся с экспериментальными данными через параметр Vd, характеризующий степень импульсности помехи [4].
Построение имитационной модели квазиимпульсной помехи производится с использованием аппроксимации выбросов огибающей помехи экспоненциальными импульсами. Основанием для выбора такой аппроксимации является экспоненциальный вид огибающей импульсной характеристики одиночного колебательного контура.
Реализация импульсной составляющей помехи формируется в системе координат с логарифмической шкалой по оси ординат путем расстановки на оси времени выбросов огибающей помехи, статистика пересечения которых (Wd (х), Wi(х)) полагается известной. Расстановка производится, начиная с самого верхнего уровня и заканчивая уровнем ближайшим к фоновому с интервалом 8-10 дБ. Сказанное иллюстрируется рисунком 1.
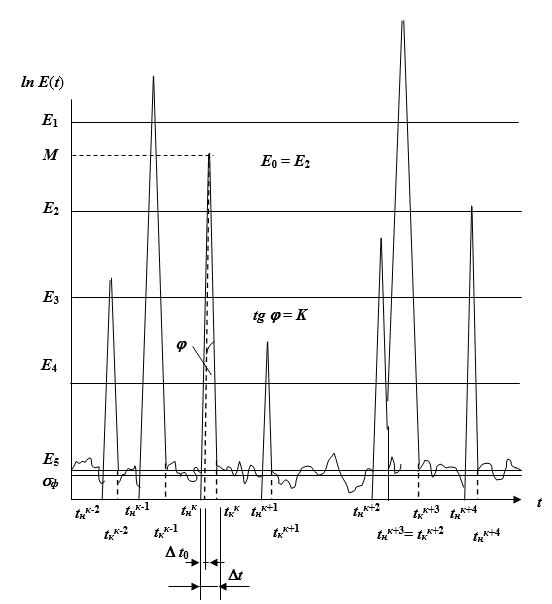
Рис. 1. Построение реализации импульсной составляющей квазиимпульсной помехи
Длительность очередного выброса импульсной составляющей помехи Dt0 на текущем уровне Е0 определяется с помощью метода Монте-Карло на основании распределения длительностей Wd(х) выбросов на данном уровне. Затем производится пересчет этой длительности в длительность импульса Dt на уровне СКО фоновой составляющей помехи sф по формуле:
Dt = Dt0 + (Е0 - sф) / К, (1)
в которой время нормировано относительно величины 
; где В - полоса пропускания приемника, а Е0 и σф - относительно СКО помехи 
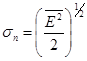. В (1) К - тангенс угла наклона гипотенузы к лежащему на оси времени основанию прямоугольного треугольника, аппроксимирующего в логарифмическом масштабе выбросы огибающей помехи, численно равный коэффициенту затухания экспоненциального импульса, который в свою очередь равен эффективной ширине полосы его спектра [3], совпадающей с полосой пропускания РПУ В.
Координаты начала (tн) и конца (tк) импульса заносятся в двумерный массив, длина которого равна числу выбросов огибающей помехи в формируемом временном интервале. Расстояние между выбросами на текущем уровне определяется на основании распределения интервалов между выбросами огибающей помехи Wi(х).
После завершения расстановки выбросов на очередном уровне аналогичным образом производится заполнение промежутков между выбросами предыдущего уровня. При этом по формуле М = К Δt0 определяется пиковое значение очередного формируемого на текущем уровне выброса, и в случае, если М больше предыдущего уровня, то, поскольку выбросы, пересекающие этот уровень, уже сформированы, импульс аннулируется, а на его месте формируется следующий. Таким образом, после заполнения последнего самого нижнего уровня получается опирающаяся на фоновый уровень последовательность выбросов огибающей импульсной составляющей помехи.
Необходимые для формирования импульсной составляющей квазиимпульсной помехи аналитические выражения распределений длительностей выбросов огибающей помехи Wd(х) и интервалов между ними Wi(х) для фиксированного уровня огибающей помехи Е0 были получены в рамках логарифмически нормальной модели [4] для односвязной марковской последовательности примыкающих друг к другу аппроксимирующих (опорных) импульсов [7]. Выражения для распределений имеют вид:
Wd(k t0) = 1 - rk++, (2) Wi (k t0) = 1 - rk--, (3)
где ρ ++ =К 
, ρ -- = 
, ρ + =F [-α (Е0)],
R0 = R (t0) = 1 + 
ln 
, (α Е0) = σ + 
ln 
,
а σ определяется выражением
где Vd = 20 lg 
= 20 lg 
, (4)
σn = 
- СКО, а 
- среднее значение огибающей помехи.
В (3) приняты следующие обозначения:
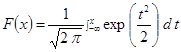, (5)
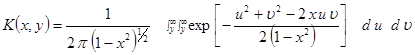- (6)
табулированные функции Лапласа и Крампа [8], Ве(t) - корреляционная функция огибающей помехи, t0 - длительность опорного импульса.
Для того чтобы аппроксимирующая последовательность импульсов была марковской, длительность аппроксимирующих импульсов t0 выбирается из условия [5] t к>> t0 или 1 / В >> t0, где tк - интервал корреляции процесса на выходе входной цепи приемника. При вычислениях было принято t0 =
. Вычисление специальных функций F(х) и К(х, у) требует больших затрат машинного времени . Воспользовавшись аппроксимацией функции F(х) из [8]: 
(7)
где 
, ρ = 0,2316419, α1 = 0,31938153, α2 = -0,35636378,
α3 = 1,781477, α4 = -1,821256, α5 = 1,3302744,
обеспечивающей точность не хуже 1,7J10-7, и разложением в ряд подынтегрального выражения в К(х, у) [8], получим выражение
, (8)
в котором мы ограничимся первыми 10 членами ряда. Учитывая связь производных функции Лапласа с полиномами Эрмита:
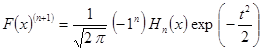, (9)
выражение для ρ ++ можно представить в виде удобном в вычислительном
отношении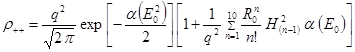 
, (10)
где 
. (11)
Энергетический спектр огибающей импульсной составляющей помехи, как это принято в [2], аппроксимируется прямоугольным треугольником с основанием В, где В - полоса пропускания входной цепи приемника. При этом выражение для R0 в (2), (3) и (9) примет вид:
R0 = 1 - 
. (12)
Таким образом, при известных типе помехи, действующей в канале связи (атмосферная, индустриальная), параметре импульсности помехи Vd, полосе пропускания входной цепи приемника В и получаемых в рамках логарифмически нормальной модели распределениях длительностей выбросов огибающей помехи Wd(x) и интервалов между ними Wi(х) описанные выше процедуры позволяют сформировать огибающую импульсной составляющей квазиимпульсной помехи. При этом фаза помехи принимается постоянной внутри выброса и распределенной равномерно в различных выбросах.
Фоновая составляющая представляет собой нормальную помеху с дисперсией, определяемой по формуле 
, где
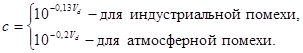
Она заполняет интервалы между выбросами импульсной составляющей. При этом в отличие от последней, формируемой заранее, отсчеты фоновой составляющей вычисляются в процессе моделирования.
Процесс формирования отсчетов импульсной составляющей помехи, алгоритм которого представлен на рисунке 2, начинается после того как массив, описывающий ее, будет заполнен, и сводится к просмотру всех моментов выборки в пределах реализации помехи.
После нахождения амплитуды и фазы помехи в отсчетной точке формируются отсчеты квадратурных компонент помехи А cos j и A sin j. Целесообразность перехода к квадратурным компонентам обусловлена тем, что в современных приемных устройствах с цифровой обработкой информации, как правило, используется квадратурный выход, что снижает требования к производительности вычислителя, так как обработка высокочастотного сигнала заменяется обработкой его низкочастотных квадратурных компонент.
Если момент выборки попадает в интервал между начальной (tн) и конечной (tк) координатами очередного выброса, то амплитуда помехи в этот момент времени определяется по формуле:
А = (tот - tк) к , (13)
где tот - момент взятия отсчета, а А - измеряется в децибелах относительно СКО помехи.
Фаза в отсчетной точке определяется на основе равномерного распределения и остается постоянной для всех отсчетов в пределах выброса. После нахождения амплитуды и фазы помехи в отсчетной точке формируются отсчеты квадратурных компонент помехи А cos φ и A sin φ.
Целесообразность перехода к квадратурным компонентам обусловлена тем, что в современных приемных устройствах с цифровой обработкой информации, как правило, используется квадратурный выход, так как это снижает требования к производительности вычислителя, поскольку обработка высокочастотного сигнала заменяется обработкой его низкочастотных квадратурных компонент.
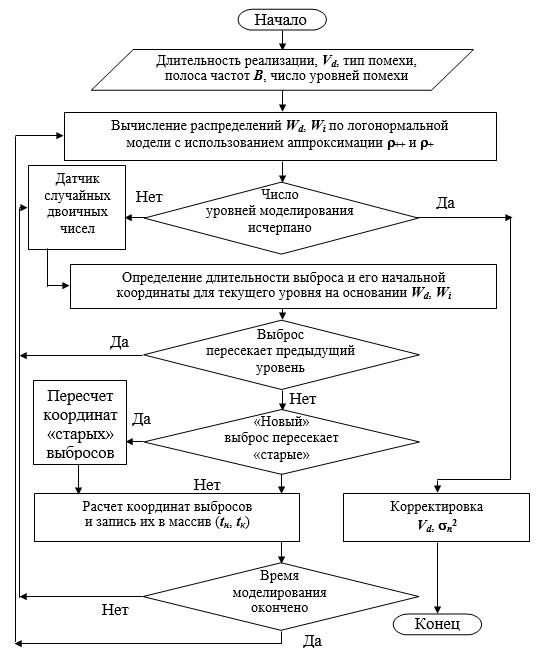
Рис. 2. Алгоритм формирования импульсной составляющей квазиимпульсной помехи
При попадании момента выборки в интервал между выбросами помехи формирование отсчетов квадратурных компонент фоновой составляющей помехи производится непосредственно из двух независимых нормальных процессов с дисперсией 
и нормированной корреляционной функцией, которая при принятой выше аппроксимации спектра огибающей помехи в виде прямоугольного треугольника с основанием В записывается:
. (14)
При этом математическое ожидание и дисперсия отсчетных значений квадратурных компонент фоновой составляющей помехи, которые берутся с интервалом Δt , определяются из выражений [8]:
т = r (Δt) х , (15) 
= 
, (15)
где х - значение квадратурной составляющей в момент выборки предыдущего отсчета.
Достоинством предлагаемого способа моделирования квазиимпульсных помех является возможность адаптации модели через параметр Vd к условиям эксплуатации приемной радиоэлектронной аппаратуры, поскольку в литературе приводятся экспериментальные данные о зависимости Vd от условий радиоприема: географического района, времени года и времени суток (для атмосферных помех), высоты точки приема (для индустриальных помех), а также от частотного диапазона и полосы пропускания приемного устройства (для обоих видов помех).
Рецензенты:
Козлов А.И., д.ф.-м.н., профессор, профессор кафедры «Технической эксплуатации радиоэлектронного оборудования воздушного транспорта» Московского государственного технического университета гражданской авиации, г. Москва;
Акиншин Р.Н., д.т.н., доцент, ведущий научный сотрудник секции по оборонным проблемам Министерства обороны (при Президиуме Российской академии наук), г. Москва.
Библиографическая ссылка
Евтушенко О.А. МОДЕЛИРОВАНИЕ ПРИБЛИЖЕННОЙ К РЕАЛЬНОЙ ПОМЕХОВОЙ ОБСТАНОВКИ ПРИ ПОЛУНАТУРНЫХ ИСПЫТАНИЯХ СРЕДСТВ СВЯЗИ, ИСПОЛЬЗУЕМЫХ ПРИ УПРАВЛЕНИИ ВОЗДУШНЫМ ДВИЖЕНИЕМ С АВТОМАТИЧЕСКИМ ЗАВИСИМЫМ НАБЛЮДЕНИЕМ // Современные проблемы науки и образования. – 2015. – № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18540 (дата обращения: 23.04.2024).