Постановка задачи
В настоящее время существует необходимость учитывать температурную зависимость сопротивления проводов, а также качество электрической энергии при расчете потерь энергии в электрических сетях [2, 4, 7, 10]. Кроме того, уточненные значения активных сопротивлений могут быть эффективно использованы при решении различных задач динамики сетей, например, при расчете перенапряжений при замыканиях на землю в сети с компенсацией емкостных токов.
Рассматриваемый подход связан с вычислением температур элементов сети на основе уравнений теплового баланса. Эти уравнения в большинстве случаев нелинейны, и для их решения могут быть использованы численные методы. Применение численных методов имеет определенные недостатки. В частности, требуются специальные компьютерные программы, возникают затруднения при анализе результатов и отсутствует возможность решения обратных задач. Поэтому на практике получили распространение различные способы упрощения уравнений теплового баланса [5, 6, 9].
Тепловой поток Q от провода в окружающую среду обусловлен конвекцией (Qк) и тепловым излучением [1] (Qл) [8]:
![]() , (1)
, (1)
где Tвнеш и Tокр – абсолютные температуры внешней поверхности провода и окружающей среды; Aк и Aл – постоянные коэффициенты; k – показатель степени, зависящий от условий конвекции.
Наиболее распространенным является случай вынужденной конвекции, поскольку провода охлаждаются на открытом воздухе. Этому соответствует k=1 [8], и нелинейность уравнений обусловлена только наличием лучистого теплообмена. Вместе с тем при слабом ветре может реализоваться также естественная конвекция. Несмотря на нетипичность этого случая, он представляет практический интерес, так как именно в такой ситуации возникают наиболее неблагоприятные условия охлаждения проводов. При естественной конвекции в общем случае k>1, а для условий, возникающих при охлаждении проводов, ![]() [5,8].
[5,8].
Самым распространенным способом упрощения уравнений является приближенное представление величины Qл квадратичной функцией температуры провода [3, 5]. Однако ранее используемые способы такого представления ориентированы, прежде всего, на расчет допустимых токовых нагрузок. Поэтому они дают удовлетворительные результаты только при максимальных рабочих температурах, и, кроме того, допускают погрешности в сторону некоторого занижения теплового потока.
При расчете потерь энергии требуется высокая точность на всем диапазоне рабочих температур. Наиболее математически обоснованным способом достижения максимальной точности является метод наименьших квадратов. В своей классической форме он относится к численным методам. Однако в данном случае исходная функция задана аналитически. Это позволяет при минимизации отклонений перейти от суммирования по конечному числу точек к интегрированию на всем заданном диапазоне, что в конечном итоге приводит к аналитическим формулам для коэффициентов аппроксимации. Решение этой задачи для условий вынужденной конвекции рассмотрено в [9]. В настоящей статье изложены результаты аналогичного преобразования уравнения для естественной конвекции.
Приведение уравнения теплового баланса к квадратичному виду
Из формулы (1) видно, что уравнение теплового баланса содержит два нелинейных слагаемых: ![]() и
и ![]() где ΔΘ – превышение температуры поверхности провода над температурой окружающей среды. Четвертую степень температуры можно расписать следующим образом:
где ΔΘ – превышение температуры поверхности провода над температурой окружающей среды. Четвертую степень температуры можно расписать следующим образом:
![]() . (2)
. (2)
Запишем нелинейную составляющую (1) в виде функции:
![]() , (3)
, (3)
где ![]()
Выполним преобразование F по методу наименьших квадратов к функции H вида:
![]() (4)
(4)
на диапазоне 0 ≤ ΔΘ ≤ ΔΘд. Выбор этого диапазона и формулы для расчета его верхней границы ΔΘд приведены в [9].
Условие преобразования F к H имеет вид:
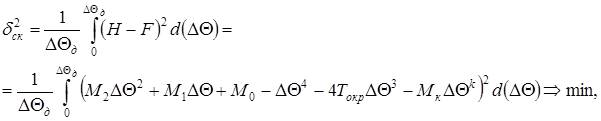 (5)
(5)
где δск – среднеквадратичная разность функций H и F.
Решение задачи (5) при ![]() приводит к следующим формулам:
приводит к следующим формулам:
![]() , (6)
, (6)
![]() , (7)
, (7)
![]() . (8)
. (8)
Полностью уравнение теплового баланса провода имеет вид [9]:
![]() (9)
(9)
где αкон – коэффициент теплоотдачи конвекцией, причем для случая вынужденной конвекции берется коэффициент вынужденной конвекции αвын, а для случая естественной конвекции – коэффициент естественной конвекции αк; εп – коэффициент черноты поверхности провода для инфракрасного излучения; C0 = 5,67·10-8 Вт/(м2·К4) – постоянная излучения абсолютно черного тела; Θвнеш – температура поверхности провода в ºC; As – поглощательная способность поверхности провода для солнечного излучения; qсолн – плотность потока солнечной радиации на провод; dпр – диаметр провода; ![]() – потери активной мощности в проводе на единицу длины при Θвнеш = 0 ºC, равные [9]
– потери активной мощности в проводе на единицу длины при Θвнеш = 0 ºC, равные [9]
 , (10)
, (10)
где I – ток в проводе; r0 – погонное активное сопротивление при ºC; Sиз – погонное тепловое сопротивление изоляции.
Используем выражение для коэффициента теплоотдачи естественной конвекцией, полученное в [6]:
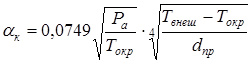 , (11)
, (11)
где Pа – атмосферное давление.
Подставим (11) в (9) с использованием коэффициентов, введенных в уравнении (1):
![]() (12)
(12)
где
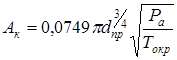 , (13)
, (13)
![]() . (14)
. (14)
Расписав в (12) ![]() по формуле (2) и произведя замену F на H, после преобразований получим уравнение:
по формуле (2) и произведя замену F на H, после преобразований получим уравнение:
![]() , (15)
, (15)
где Θокр – температура окружающей среды в ºC.
В (15) введены следующие обозначения:
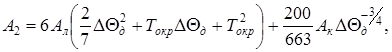 (16)
(16)
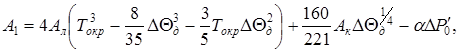 (17)
(17)
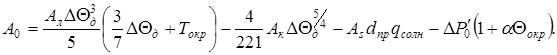 (18)
(18)
Уравнение (15) представляет собой уравнение теплового баланса провода, приведенное к квадратичному виду. Его решение имеет вид:
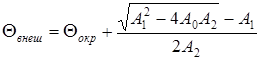 . (19)
. (19)
Второй корень уравнения является посторонним, поскольку может давать Θвнеш < Θокр, что противоречит физическому смыслу решаемой задачи.
Потери активной мощности на единицу длины провода и температура токоведущей жилы равны:
![]() , (20)
, (20)
![]() . (21)
. (21)
Анализ результатов
С практической точки зрения критерием эффективности проведенной аппроксимации является точность вычисления температуры провода и потерь активной мощности. Однако эти величины зависят от многих факторов. Поэтому путем численного анализа трудно установить, насколько «типичны» получающиеся результаты. Чтобы исключить эти факторы, сначала проанализируем точность аппроксимации теплового потока Q, определяемого по формуле (1). Для уменьшения количества коэффициентов разделим его на величину Aл:
![]() . (22)
. (22)
Аппроксимированный аналог этой функции получается путем подстановки (2) в (22) и замены F на H:
![]() . (23)
. (23)
Функция ![]() однозначно задается двумя параметрами: Tокр и Mк. Чем ниже температура окружающей среды, тем шире диапазон аппроксимации, и, следовательно, можно ожидать увеличения погрешности. Поэтому примем достаточно низкое значение этой температуры Tокр = 275 K.
однозначно задается двумя параметрами: Tокр и Mк. Чем ниже температура окружающей среды, тем шире диапазон аппроксимации, и, следовательно, можно ожидать увеличения погрешности. Поэтому примем достаточно низкое значение этой температуры Tокр = 275 K.
Исходя из (3), (13) и (14), найдем:
 (24)
(24)
Видно, что значение Mк определяется главным образом диаметром провода dпр и коэффициентом черноты εп. Влияние атмосферного давления и температуры окружающей среды менее существенно: варьирование этих величин в реальных пределах приводит к изменению Mк примерно на 10 %.
Выберем значения коэффициента черноты для поверхности провода: минимальное (для неизолированных проводов) значение εп = 0,5 принято в [11], а максимальное (для изолированных проводов) εп = 0,8 в [3]. Диаметр может изменяться от 4,5 мм провода АС-10/1,8 до 30,6 мм провода АС-500/64 у неизолированных проводов и от 11,5 мм провода SAX-35 до 22,8 мм провода SAX-240 [1] . Выполним расчеты потока теплового излучения отдельно для неизолированных и изолированных проводов по уравнениям (22) и (23). Давление на высоте 300 метров над уровнем моря принимаем 100 кПа.
Верхнюю границу диапазона преобразования зададим соотношением:
![]() , (25)
, (25)
где ΔΘиз – перепад температуры в изоляции провода (при ее наличии). Расчет для изолированных проводов SAX разных сечений дает ΔΘиз=6,7…10,2 °C. В качестве типичного значения можно использовать ΔΘиз=8 °C. Примем для изолированного провода: ![]() К ,
К , ![]() К. Тогда согласно формуле (25) Tокр = 275 K. У неизолированных проводов величина ΔΘд должна быть несколько меньше. Тем не менее, в дальнейшем для лучшей сравнимости результатов используется только ΔΘд = 80 °C. Это эквивалентно некоторому расширению диапазона аппроксимации для неизолированных проводов, что вполне допустимо при сравнительных расчетах.
К. Тогда согласно формуле (25) Tокр = 275 K. У неизолированных проводов величина ΔΘд должна быть несколько меньше. Тем не менее, в дальнейшем для лучшей сравнимости результатов используется только ΔΘд = 80 °C. Это эквивалентно некоторому расширению диапазона аппроксимации для неизолированных проводов, что вполне допустимо при сравнительных расчетах.
Результаты сравнительных расчетов потока теплового излучения для неизолированных и изолированных проводов представлены в таблицах 1 и 2 соответственно. Для минимального и максимального диаметров проводов погрешности определения величин теплового потока по приближенному уравнению Qаппр1, Qаппр2 относительно расчета по исходному уравнению ![]() ,
, ![]() обозначены δаппр1 и δаппр2 соответственно.
обозначены δаппр1 и δаппр2 соответственно.
Таблица 1
Результаты сравнительных расчетов потока теплового излучения провода для варианта расчета с неизолированными проводами
|
ΔΘ, °C |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
|
|
43,38 |
100,8 |
165,9 |
236,9 |
313,0 |
393,6 |
478,3 |
567,0 |
|
|
30,21 |
69,50 |
113,9 |
162,5 |
214,6 |
270,0 |
328,4 |
389,9 |
|
Qаппр1,108∙K4 для dпр =4,5 мм |
44,65 |
103,0 |
166,9 |
236,4 |
311,5 |
392,2 |
478,4 |
570,2 |
|
Qаппр2,108∙K4 для dпр =30,6 мм |
30,99 |
70,80 |
114,5 |
162,1 |
213,7 |
269,1 |
328,5 |
391,7 |
|
δаппр1, % |
-2,86 |
-2,11 |
-0,59 |
0,23 |
0,49 |
0,37 |
-0,012 |
-0,56 |
|
δаппр2, % |
-2,52 |
-1,83 |
-0,45 |
0,20 |
0,42 |
0,31 |
-0,014 |
-0,47 |
Таблица 2
Результаты сравнительных расчетов потока теплового излучения провода для варианта расчета с изолированными проводами
|
ΔΘ, °C |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
|
|
25,9 |
59,23 |
96,88 |
138,0 |
182,3 |
229,4 |
279,2 |
331,8 |
|
|
23,2 |
52,83 |
86,27 |
122,8 |
162,2 |
204,1 |
248,6 |
295,6 |
|
Qаппр1,108∙K4 для dпр =11,5 мм |
26,5 |
60,23 |
97,32 |
137,8 |
181,6 |
228,7 |
279,3 |
333,2 |
|
Qаппр2,108∙K4 для dпр =22,8 мм |
23,7 |
53,66 |
86,62 |
122,6 |
161,6 |
203,6 |
248,7 |
296,7 |
|
δаппр1, % |
-2,34 |
-1,67 |
-0,45 |
0,19 |
0,38 |
0,28 |
-0,015 |
-0,42 |
|
δаппр2, % |
-2,19 |
-1,54 |
-0,40 |
0,18 |
0,35 |
0,25 |
-0,015 |
-0,38 |
Из приведенных выше таблиц следует, что погрешности аппроксимации теплового потока излучения предложенным методом не превышают трех процентов. Проведенные исследования также показали, что уравнение (19) имеет при скорости ветра 0,2 м/с высокую точность по сравнению с зарубежным методом CIGRE: относительная погрешность потерь активной мощности не превышает 1 %, а абсолютные погрешности температуры – 3 градусов.
Таким образом, разработанный метод аппроксимации дает высокую точность на всем диапазоне температур и может быть использован при расчете потерь энергии и выборе мероприятий по их снижению.
Рецензенты:
Харламов В. В., д.т.н., профессор, заведующий кафедрой Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Омский государственный университет путей сообщения», г. Омск;
Сидоров О. А., д.т.н., профессор, заведующий кафедрой Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Омский государственный университет путей сообщения», г. Омск.
[1] Здесь подразумевается не тепловое излучение собственно провода, а результирующий поток энергии с учетом излучения окружающих тел.
Библиографическая ссылка
Гиршин С.С. ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОВОГО БАЛАНСА ПРОВОДОВ ВОЗДУШНЫХ ЛИНИЙ ПРИ ТЕПЛООТДАЧЕ ЕСТЕСТВЕННОЙ КОНВЕКЦИЕЙ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18505 (дата обращения: 12.03.2026).



