При расчете потерь электрической энергии все чаще обосновывается необходимость учета температурной зависимости активных сопротивлений [1–7]. Такой подход предполагает вычисления значений температур элементов электрической сети на основе использования уравнения теплового баланса. С целью упрощения базового уравнения в условиях вынужденной конвекции в работе [5] использовался метод наименьших квадратов. В данной работе метод применяется в условиях естественной конвекции и изложены результаты проверки полученных соотношений.
Уравнение теплового баланса может быть представлено в следующем виде [5]:
![]() (1),
(1),
где Tвнеш и Tокр – абсолютные температуры внешней поверхности провода и окружающей среды; αкон – коэффициент теплоотдачи конвекцией, причем для случая вынужденной конвекции берется коэффициент вынужденной конвекции αвын, а для случая естественной конвекции – коэффициент естественной конвекции αк; ![]() – температурный коэффициент сопротивления; εп – коэффициент черноты поверхности провода для инфракрасного излучения; C0 = 5,67·10-8 Вт/(м2·К4) – постоянная излучения абсолютно черного тела; Θвнеш – температура поверхности провода в ºC; As – поглощательная способность поверхности провода для солнечного излучения; qсолн – плотность потока солнечной радиации на провод; dпр – диаметр провода;
– температурный коэффициент сопротивления; εп – коэффициент черноты поверхности провода для инфракрасного излучения; C0 = 5,67·10-8 Вт/(м2·К4) – постоянная излучения абсолютно черного тела; Θвнеш – температура поверхности провода в ºC; As – поглощательная способность поверхности провода для солнечного излучения; qсолн – плотность потока солнечной радиации на провод; dпр – диаметр провода; ![]() – потери активной мощности в проводе на единицу длины при Θвнеш = 0 ºC, равные [5]:
– потери активной мощности в проводе на единицу длины при Θвнеш = 0 ºC, равные [5]:
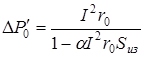 , (2)
, (2)
где I – ток в проводе; r0 – погонное активное сопротивление при ºC; Sиз – погонное тепловое сопротивление изоляции.
Используем выражение для коэффициента теплоотдачи естественной конвекцией, полученное в [4]:
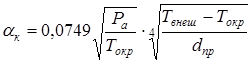 , (3)
, (3)
где Pа – атмосферное давление.
Подставив (3) в (1), имеем:
![]() (4)
(4)
где:
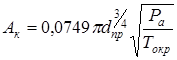 , (5)
, (5)
![]() . (6)
. (6)
Расписав в (4) ![]() по формуле:
по формуле:
![]() , (7)
, (7)
и применив метод наименьших квадратов, после преобразований получим уравнение:
![]() , (8)
, (8)
где Θокр – температура окружающей среды в ºC.
В (8) введены следующие обозначения:
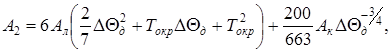 (9)
(9)
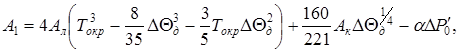 (10)
(10)
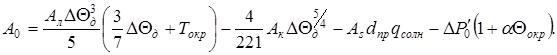 (11)
(11)
Уравнение (8) представляет собой уравнение теплового баланса провода, приведенное к квадратичному виду. Его решение имеет вид:
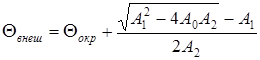 . (12)
. (12)
Второй корень уравнения является посторонним, поскольку может давать Θвнеш < Θокр, что противоречит физическому смыслу решаемой задачи.
Потери активной мощности на единицу длины провода равны:
![]() . (13)
. (13)
Температура токоведущей жилы:
![]() . (14)
. (14)
Верхнюю границу диапазона преобразования для неизолированных проводов зададим соотношением:
![]() , (15)
, (15)
где ![]() – допустимая температура токоведущей жилы.
– допустимая температура токоведущей жилы.
Для проверки достоверности расчетов приведем результаты сравнительных расчетов температуры, вычисленной по приближенному уравнению (12) и исходному уравнению (1), а также по международному методу CIGRE [8], созданному на основе стандарта расчета линий электропередачи, разработанного Международным Советом по большим электроэнергетическим системам. Расчет потерь активной мощности производился по формуле (13).
Вычисление по уравнению (1) производились на основе использования метода последовательных приближений при условии вынужденной конвекции.
Для провода марки 429-AL1/56-ST1 исходные данные (за исключением тока и скорости ветра) приведены в таблице 1 [9], а результаты расчетов – в таблице 2.
Глобальная солнечная радиация рассчитывалась по следующей формуле:
![]() , (16)
, (16)
где qs.пр – плотность потока прямой солнечной радиации на поверхность, перпендикулярную солнечным лучам; qs.расс – плотность потока рассеянной солнечной радиации, осредненная по всем направлениям; kзт – понижающий коэффициент, учитывающий затененность участков провода (коэффициент затененности); js – угол между осью провода и направлением солнечных лучей.
Расчет прямой и рассеянной составляющих солнечной радиации для исходного уравнения (1) проводился с учетом высокогорной местности, для которой можно приближенно принять соотношение прямой и рассеянной составляющих солнечной радиации 1/11. С учетом этого из [9] возьмем значение прямой составляющей ![]() Вт/м2, а рассеянной
Вт/м2, а рассеянной ![]() Вт/м2. Коэффициент затененности принят kзт=0,6, а угол между осью провода и направлением солнечных лучей js=
Вт/м2. Коэффициент затененности принят kзт=0,6, а угол между осью провода и направлением солнечных лучей js=![]() .
.
Для удобства анализа введены обозначения:
![]() ,
, ![]() – абсолютные погрешности расчета температуры провода приближенным методом;
– абсолютные погрешности расчета температуры провода приближенным методом;
![]() – абсолютная погрешность расчета температуры провода по исходному уравнению (1);
– абсолютная погрешность расчета температуры провода по исходному уравнению (1);
![]() ,
, ![]() – относительная погрешность расчета потерь мощности по приближенному уравнению (12) по сравнению с расчетами по исходному уравнению (1) и зарубежному методу CIGRE;
– относительная погрешность расчета потерь мощности по приближенному уравнению (12) по сравнению с расчетами по исходному уравнению (1) и зарубежному методу CIGRE;
![]() – относительная погрешность расчета потерь мощности по исходному уравнению (1) по сравнению с методом CIGRE.
– относительная погрешность расчета потерь мощности по исходному уравнению (1) по сравнению с методом CIGRE.
Погрешности определялись по следующим формулам:
![]() , (17)
, (17)
![]() , (18)
, (18)
![]() , (19)
, (19)
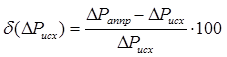 , (20)
, (20)
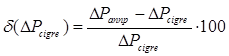 , (21)
, (21)
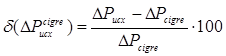 , (22)
, (22)
где ![]() – значение температуры провода по приближенному уравнению (12), ºC;
– значение температуры провода по приближенному уравнению (12), ºC; ![]() – температура провода по исходному уравнению (1), ºC;
– температура провода по исходному уравнению (1), ºC; ![]() – температура провода по методу CIGRE, ºC;
– температура провода по методу CIGRE, ºC; ![]() – активные потери мощности, рассчитанные с помощью приближенного метода, Вт/м;
– активные потери мощности, рассчитанные с помощью приближенного метода, Вт/м; ![]() – активные потери мощности, рассчитанные с помощью исходного метода, Вт/м;
– активные потери мощности, рассчитанные с помощью исходного метода, Вт/м; ![]() – активные потери мощности, рассчитанные с помощью метода CIGRE, Вт/м.
– активные потери мощности, рассчитанные с помощью метода CIGRE, Вт/м.
Таблица 1
Исходные данные для решения уравнений теплового баланса
|
Наименование и обозначение параметра |
Численное значение |
|
Погонное активное сопротивление при 0 ºC r0 |
0,0000624 Ом/м |
|
Температурный коэффициент сопротивления a |
0,00403 ºC-1 |
|
Диаметр провода dпр |
0,0286 м |
|
Коэффициент теплоотдачи вынужденной конвекцией при первом варианте расчета αвын |
6,1557 Вт/(м2∙K) |
|
Коэффициент теплоотдачи вынужденной конвекцией при втором варианте расчета αвын |
9,3303 Вт/(м2∙K) |
|
Степень черноты поверхности провода εп |
0,5 |
|
Поглощательная способность поверхности провода для солнечного излучения As |
0,5 |
|
Температура окружающей среды Θокр |
40 ºC |
|
Суммарная солнечная радиация qсолн |
632,9 Вт/м2 |
|
Допустимая температура токоведущей жилы Θдоп |
90 ºC |
|
Атмосферное давление на высоте 1600 м, кПа |
81,3 |
При этих данных по формуле (15) получаем ΔΘд = 50 °C.
Таблица 2
Результаты решения уравнений теплового баланса
|
I, А |
600 |
650 |
|
|
Скорость ветра, м/с |
0,2 |
0,4 |
|
|
Расчет по приближенному уравнению (12) |
|
81,8 |
86,0 |
|
|
29,86 |
35,49 |
|
|
Расчет по исходному уравнению (1) для вынужденной конвекции |
|
77,5 |
76,0 |
|
|
29,47 |
34,42 |
|
|
Расчет по методу CIGRE
|
|
78,8 |
74,0 |
|
|
29,59 |
34,21 |
|
|
Погрешности
|
|
4,3 |
10,0 |
|
|
3,0 |
12,0 |
|
|
|
1,3 |
2,0 |
|
|
|
1,32 |
3,11 |
|
|
|
0,91 |
3,74 |
|
|
|
-0,41 |
0,61 |
|
Как следует из таблицы 2, несоответствие температуры, найденной для скорости ветра 0,2 м/с по приближенному уравнению для естественной конвекции, по сравнению с исходным уравнением для вынужденной и методом CIGRE, не превышает 5°C. Необходимо отметить, что приближенное уравнение достаточно точно определяет температуру провода при низкой скорости ветра, когда конвекцию можно считать естественной. В то же время при скорости ветра 0,4 м/с наблюдаются более существенные отличия: погрешности нахождения температуры провода по приближенному методу больше 10 °C. Этот факт обусловлен не погрешностями аппроксимации, а тем, что данный метод не учитывает скорость ветра; при расчете по исходному уравнению для вынужденной конвекции, то есть с учетом скорости ветра, погрешность относительно метода CIGRE снижается до 2 °C. Что касается определения потерь активной мощности, то, как следует из таблицы 2, для этой цели предлагаемый приближенный метод может быть реализован с высокой точностью. Исходное уравнение показывает высокую точность по сравнению с зарубежным методом CIGRE: относительная погрешность потерь активной мощности не превышает 1 %.
Рецензенты:
Харламов В.В., д.т.н., профессор, заведующий кафедрой «Электрические машины и общая электротехника» Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Омский государственный университет путей сообщения», г. Омск;
Сидоров О.А., д.т.н., профессор, заведующий кафедрой «Электроснабжение железнодорожного транспорта» Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Омский государственный университет путей сообщения», г. Омск.
Библиографическая ссылка
Горюнов В.Н., Гиршин С.С., Кузнецов Е.А., Петрова Е.В. АНАЛИЗ ПОГРЕШНОСТЕЙ РАСЧЕТА ТЕМПЕРАТУРЫ И ПОТЕРЬ МОЩНОСТИ ПО БАЗОВОМУ И ПРИБЛИЖЕННОМУ УРАВНЕНИЯМ ТЕПЛОВОГО БАЛАНСА ВОЗДУШНЫХ ЛИНИЙ ЭЛЕКТРОПЕРЕДАЧ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18494 (дата обращения: 12.03.2026).



