Оптический вихри, дислокации волнового фронта, фазовые сингулярности, точки ветвления фазовой функции – вот перечень названий, которыми обозначаются одни и те же объекты исследования. Оптический вихрь проявляет себя как изолированный минимум в поперечном распределении интенсивности некоторых типов лазеров, в спекл-картине рассеянного шероховатой поверхностью или преломленного турбулентной атмосферой лазерного излучения [3, 4]. Каждой такой точке может быть сопоставлен топологический заряд, который представляет собой число (положительное или отрицательное), равное 2π радиан [5, 1]. Эта величина возникает как результат суммирования градиента фазы вдоль замкнутого контура, окружающего область с минимальной интенсивностью. Волновой фронт в окрестности оптического вихря имеет геликоидальную структуру, поэтому из-за неопределенности фазы в центре вихря интенсивность должна быть точным нулем, а не просто локальным минимумом. Изучение оптических вихрей стало предметом сформировавшегося в последние десятилетия нового направления в оптике, названного сингулярной оптикой [1÷6]. Одной из задач, решаемых в данной области, является определение наличия оптического вихря в пучке и его координат.
Численная модель распространения излучения
Для анализа процесса зарождения дислокаций и построения алгоритма их регистрации была построена численная модель, в которой распределение амплитуды E0(x, y) одномодового пучка в плоскости апертуры источника задавалось формулой:
![]()
в которой x, y – координаты в плоскости, перпендикулярной направлению распространения; A0 – значение амплитуды при x = 0, y = 0; a0 – начальный радиус пучка; n – число (обычно, целое), характеризующее степень супергауссовости пучка. Если n = 2, пучок гауссовский, при больших значениях этой величины он имеет супергауссовскую форму (более плоская, по сравнению с гауссовским, вершина). В соответствии с этим комплексная амплитуда светового поля на входе в среду определяется как:
![]()
В приближении квазиоптики распространение пучка с комплексной амплитудой E(x,y,z) в неискажающей среде может быть описано дифференциальным уравнением вида:
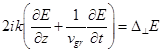
где x, y – координаты в плоскости, перпендикулярной направлению распространения пучка; z – координата в направлении распространения; ![]() – оператор Лапласа;
– оператор Лапласа; ![]() – групповая скорость. При решении задачи была проведена операция обезразмеривания, в которой координаты x и y были нормированы на начальный радиус пучка, а координата z – на дифракционную длину излучения. Численное решение уравнения квазиоптики осуществлялось с использованием быстрого преобразования Фурье.
– групповая скорость. При решении задачи была проведена операция обезразмеривания, в которой координаты x и y были нормированы на начальный радиус пучка, а координата z – на дифракционную длину излучения. Численное решение уравнения квазиоптики осуществлялось с использованием быстрого преобразования Фурье.
Определение координат оптического вихря как точек ветвления интерференционных полос
В неискажающей среде задача определения координат особых точек решается достаточно просто. Для этого может быть использовано следующее свойство: при интерференции лазерного пучка, несущего оптический вихрь, с гауссовским пучком, в полученной картине наблюдается ветвление интерференционных полос [2]. Зарегистрированная в численном эксперименте интерференционная картина, соответствующая вихрю первого порядка, приводится на рис. 1. Можем видеть, что ветвление полос хорошо выражено (рис. 1), поэтому координаты особой точки легко находится.
Значительно сложнее определить особую точку в интерференционной картине пучка, распространяющегося в турбулентной атмосфере (рис. 2). В этом случае интенсивность полос значительно отличается и ветвление, хотя и заметное визуально, достаточно сложно определяется алгоритмически. Поэтому первоначально разработанный нами алгоритм, в котором проводился анализ полной интерференционной картины, имел настолько малую точность, что практически не мог быть использован.

Рис.1. Интерференционная картина пучка, имеющего искусственную дислокацию в фазовом профиле
а  б
б
Рис. 2. Фазовый экран (а) и интерференция пучка, прошедшего данный экран (б)
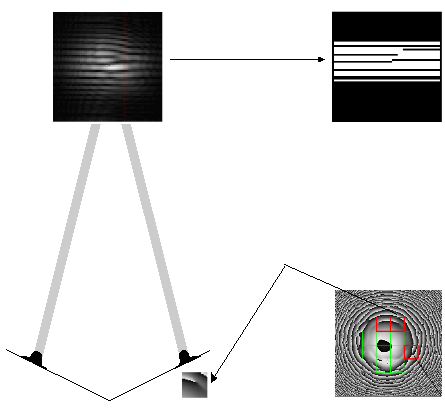
Рис. 3. Алгоритм локализации дислокаций, основанный на анализе интерференционной картины
Для повышения его точности была предложена следующая модификация метода. В численной модели оптической системы вся область анализа разбивалась на квадраты. Фаза, попадающая в пределы каждого из квадратов, присваивалась гауссовскому пучку, для которого регистрировалась интерференционная картина. Изображение подвергалось скелетонизации: по определенному уровню интенсивность полос задавалась равной единице, ниже этого уровня интенсивность была равна нулю. Схематически выполнение этих операций показано на рис. 3. В полученном «скелете» интерферограммы находились точки ветвления. При обнаружении таких точек полагалось, что в соответствующем квадрате имеется дислокация. При отсутствии ветвления дислокаций в квадрате нет. Точность метода зависит от размеров области, в пределах которой фаза присваивалась пучку.
Точность предложенного метода
Проверка точности метода была проведена следующим образом: в волновой фронт излучения вносилось определенное число особых точек первого порядка, пучок проходил кроткое (по сравнению с дифракционной длиной) расстояние, затем дислокации регистрировались на основе предложенного алгоритма. Зависимость точности от числа оптических вихрей и размеров контура интегрирования иллюстрируется данными таблицы 1, где приводится усредненное число дислокаций, определенное с использованием алгоритма. Основная особенность предлагаемого подхода – это уменьшение точности, наблюдаемое как при увеличении размеров контура интегрирования, так и при увеличении числа особых точек. Так, для контура, сторона которого равна 0,12d0 (d0 – начальный диаметр пучка) с точностью 100% регистрируется 10 введенных в начальный волновой фронт оптических вихрей, но при 50 особых точках точность составляет только 84%. Аналогичное уменьшение точности наблюдается и для других размеров, причем, чем больше контур, тем меньше точность алгоритма регистрации.
Таблица 1
Точность регистрации оптических вихрей в численном эксперименте
|
Число заданных дислокаций |
10 |
20 |
30 |
40 |
50 |
|
|
Размер контура 0,12d0
|
Число зарегистрированных дислокаций |
10 |
18 |
26 |
34 |
42 |
|
Точность регистрации, % |
100 |
90 |
87 |
85 |
84 |
|
|
Размер контура 0,18d0
|
Число зарегистрированных дислокаций |
10 |
18 |
26 |
32 |
39 |
|
Точность регистрации, % |
100 |
90 |
87 |
80 |
78 |
|
|
Размер контура 0,24d0
|
Число зарегистрированных дислокаций |
9 |
16 |
22 |
27 |
32 |
|
Точность регистрации, % |
90 |
80 |
73 |
68 |
64 |
|
Данные таблицы иллюстрируют удовлетворительную (на уровне 90-100%) точность регистрации 10 особых точек. При увеличении числа дислокаций точность метода снижается.
Зарождение дислокаций при задании начальной фазы пучка полиномами Цернике
Так как изменения фазового профиля пучка при распространении в атмосфере достаточно часто аппроксимируют набором низших полиномов Цернике, для изучения особенностей образования особых точек в турбулентной среде была проведена серия численных экспериментов, в которых начальная фаза задавалась одним из таких полиномов. В первом из экспериментов в профиль начальной фазы ![]() гауссовского пучка была введена кома, т.е. аберрация, задаваемая выражением:
гауссовского пучка была введена кома, т.е. аберрация, задаваемая выражением:
![]() ,
,
где a – коэффициент, задающий «интенсивность» искажений, c – константа, входящая в уравнение. Соответствующие распределения фазового профиля в различных плоскостях трассы распространения показаны на рис. 4 (Z = 0 – 0,4). На рисунке видно, что на малых расстояниях (Z = 0,2), как и в плоскости Z = 0, профили остаются гладкими, хотя в распределении фазы образуются характерные складки (рис. 4б). При дальнейшем распространении (Z = 0,4) складки, образовавшиеся в фазе, разрываются, и появляются точки, в окрестности которых функция испытывает разрывы, а алгоритм регистрации дислокаций определяет наличие двух оптических вихрей в пучке. Таким образом, задание начальной фазы в виде несимметричного относительно центра пучка полинома привело к появлению особых точек в волновом фронте излучения.
 (а)
(а)  (б)
(б)  (в)
(в)
Рис. 4. Распределение фазы пучка на расстоянии Z = 0 (а), Z = 0,2 (б), Z = 0,4 (в) дифракционной длины при задании начального фазового профиля комой.
Исследование также показало, что симметричные полиномы второго порядка такие как фокусировка и астигматизм не позволяют получить оптические вихри. Задание фазы с использованием сферической аберрации
![]()
также не приводит к появлению дислокаций в случае, если пучок расположен симметрично относительно центра системы координат, в которой задан полином. Но, если центр пучка сместить из точки (0, 0), будут появляться снова фазовые разрывы, а алгоритм будет регистрировать наличие вихрей в точках их окончания.
Данные настоящего параграфа показывают, что асимметрия фазового профиля, заданного полиномами третьего и более высоких порядков приводит к появлению особых точек в лазерном пучке.
Заключение
В статье описан разработанный авторами алгоритм регистрации оптических вихрей, в котором для локализации дислокаций используется ветвление полос интерференционной картины излучения. Точность алгоритма определяется размерами области, на которые разбивается область регистрации, и числом особых точек. При 10-20 дислокациях точность составляет не менее 90%.
Также нужно отметить, что при задании начального фазового профиля полиномами Цернике при распространении пучка в неискажающей среде в нем появляются оптические вихри.
Рецензенты:
Новиков С.А,, д.ф.-м.н, профессор Национального исследовательского Томского политехнического университета, г. Томск;
Исаев Ю.Н., д.ф.-м.н, профессор Национального исследовательского Томского политехнического университета, г. Томск.
Библиографическая ссылка
Канев Ф.Ю., Макенова Н.А. МЕТОД ОПРЕДЕЛЕНИЯ КООРДИНАТ ОСОБЫХ ТОЧЕК ВОЛНОВОГО ФРОНТА ПО ВЕТВЛЕНИЮ ПОЛОС ИНТЕРФЕРЕНЦИОННОЙ КАРТИНЫ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18427 (дата обращения: 12.03.2026).



