Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Современные инфокоммуникационные сети формируют единое пространство для обеспечения потребностей пользователей в доступе к различным информационным ресурсам. С целью реализации глобального доступа к таким ресурсам широко используются технологии спутниковых сетей связи. Существующие технологии предоставления услуг связи в спутниковых сетях имеют множество ограничений, которые на сегодняшний день не позволяют на равных конкурировать с наземными сетями. Таким ограничениями являются [2,3,8,9]: низкая пропускная способность, большие задержки линии и коммутации (маршрутизации), что обусловлено спецификой построения спутниковых систем передачи информации.

Перспективные технологии спутниковых сетей предполагают снижение влияния вышеуказанных недостатковпутем использования более широкополосных радиочастотных диапазонов [3,9], применения низкоорбитальных спутниковых группировок [2,3], переноса функций коммутации и маршрутизации на орбиту [2,3,8], повсеместном внедрении межспутниковых линий [1-3,8].Реализация данных подходов к построению спутниковых сетей связи позволит обеспечить единое глобальное инфокоммуникационное пространство необходимыми транспортными механизмами.

1.      Предварительные сведения

Исследуемая в данной работе перспективная спутниковая сеть передачи информации состоит из четырех равноправных спутниковых систем (рис.1а). Спутниковые системы взаимодействуют друг с другом путем использования межспутниковых линий передачи [1-3,8]. Предполагается, что спутники используют средневысотные или низкие орбиты для снижения времени задержки.

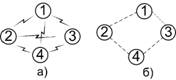
Рис.1.Структура исследуемой сети

При необходимости, спутниковая сеть может быть построена по полносвязнойтопологии «каждый с каждым», но в связи с изменяющимися условиями совместного расположения и состояния среды передачи, происходит изменение структуры сети передачи информации. Например, на рис. 1б представлен случай, когда линия между спутниковыми системами 2 и 3 недоступна и тогда связность узлов 1 и 4 будет обеспечиваться организацией обходных маршрутов через узлы 2 и 3. Таким образом, задача состоит в создании модели спутниковой сети, позволяющей в реальном масштабе времени отражать состояние данной сети с целью осуществления возможности по снижению перегрузки сети путем перераспределения трафика по узлам сети.

Исследуемая спутниковая сеть представляет собой несколько систем, связанных беспроводными каналами связи, что, естественно, приводит к тому, что структура данной сети является динамически изменяющейся и задача анализа распределения трафика в такой сети значительно усложняется. Это связано, во-первых, с тем, что оценка распределения трафика в сети обычно производится методами теории массового обслуживания без учета структурных параметровсети; а во-вторых, с плохой формализуемостьютакихметодов.

Более того, при организации сети передачи данных с динамически изменяющейся топологией необходимо учесть взаимодействие структуры сети и информационных потоков. Учет процессно-структурного взаимодействия классическими методами исследования обычно не производится [4], так как в основном для исследования сетей связи используются теория графов и теория массового обслуживания. Теория графов позволяет исследовать структуру сети без учета влияния процесса обработки информации, а теория массового обслуживания обеспечивает получение вероятностно-временных характеристик систем с неформализованным учетом влияния структуры.

Рассматриваемый в данной работе метод моделирования распределения потоков в перспективных спутниковых сетях позволяет решить задачу учета процессно-структурного взаимодействия с использованием тензорного подхода. При этом обеспечивается хорошая формализация предлагаемого метода [5].

2.      Тензорная модель исследуемой сети.

В качестве инварианта использовано выражение загрузки [7], как произведение средней длительности обслуживания на интенсивность потоков в системах распределения информации:В таком случае, исходными данными являются предварительные загрузки систем распределения информации и средняя длительность обслуживания. Использование данного метода позволяет найти распределение интенсивностей потоков по сети с учетом ее топологии.

В данном методе рассматривается модель сети, обладающая структурой, состоящей из замкнутых путей (контуров), которая определена, как структура исходной сети. Уравнение поведения исходной сети записывается, как:

Примитивная сеть является декомпозиционной относительно исходной сети модели, является контурной (рис. 2: − интенсивности информационных потоков, − загрузки систем распределения информации, − средняя длительность обслуживания) и состоит из несвязанных контуров. Уравнение поведения примитивной сети записывается, как:  Количество систем () в примитивной сети равно количеству систем в исходной сети.

Рис.2. Пример примитивной контурной сети

Геометрическими объектами, необходимыми для описания такой примитивной сети, являются: вектор интенсивности потоков вызовов в системах  вектор загрузки систем распределения информации  тензор средней длительности обслуживания  Тогда, уравнение состояния для примитивной сети, в общем случае, имеет вид:

Вспомогательная сеть обеспечивает учет структуры исходной сети при объединении систем примитивной сети и для исследуемых сетей также содержит информацию о путях передачи трафика. Возбуждение вспомогательной сети производится контурными интенсивностями , вызывающими в сети отклик в виде загрузок сети  Уравнение поведения вспомогательной сети записывается, как:  Во вспомогательной системе координат исходная контурная сеть заменяется контурной сетью, которая формируется при объединении систем, составляющих примитивную сеть.

Далее, необходимо определить тензор и формулы преобразования. Тензор преобразования это геометрический объект, связывающий переменные примитивной и вспомогательной сети. Уравнение преобразования тогда записывается, как: или , где  – вектор интенсивности поступления вызовов для примитивной сети; – вектор контурных интенсивностей поступления вызовов; – тензор преобразования интенсивностей потоков.Тензор преобразования определяет преобразование координат при переходе от примитивной к вспомогательной системе.

Элементы строкитензора  показывают контурные потоки, проходящие через систему распределения информации, элементы  столбца содержат информацию о системах, входящих в  контур. Для оценки вероятностно-временных характеристик исследуемой сети необходимо рассматривать контуры, как пути передачи информации от генератора пакетов или сообщений (источник) к приемнику (получателю) информации.

Для нахождения элементов матрицы преобразования в вспомогательной сети рассматриваются контурные интенсивности потоков контуров и для каждой системы они выражаются через интенсивности примитивной сети в соответствии с их местом в исходной.

При этом, для вспомогательной сети уравнение состояния приобретает вид:  В общем виде уравнение может быть записано, как:

В связи с тем, что в общем случае модели сетей связи являются ортогональными, то предварительно необходимо привести структуру модели к контурному виду. Для этого необходимо ввести мнимые системы, которые будут обеспечивать выполнение условия и сформируют замкнутые контуры между источником и получателем (в качестве примера рис. 3: система 1 – источник, система 8 – получатель, система 25 – мнимая). В таком случае, тензор преобразования может быть представлен в ви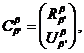де:  где  описывает участие реальных систем в организации путей,  описывает участие мнимых ветвей.

Для установления формул преобразования геометрических объектов используются следующие предположения. Во-первых, что поток вызовов с одной и той же интенсивностью поступления вызовет при неизменной интенсивности обслуживания одну и ту же загрузкуустройств при изменении структуры и можно считать, что будет выполняться соотношение (инвариант) : где переменные со штрихом для вспомогательной структуры сети (содержащей информацию о топологии исходной сети), без штриха для декомпозиционной структуры сети (примитивной сети). Во-вторых, объединение систем в единую сеть не вызывает никаких изменений процесса обслуживания информационного потока, т.е. тогда анализ любой сложной системы (сети) будет связан с определением простейшего элемента, его свойств и переносом алгоритма анализа на всю сложную систему (сеть). В-третьих, изменение структуры сети не предполагает качественное изменение основных соотношений между физическими величинами, описывающими простейший элемент, а определяет только их численное изменение.В тензорной нотации используемый инвариант записывается, как:  Топология исходной сети учитывается путем использования тензора преобразования  связывающего интенсивности поступления в системы примитивной сети и интенсивности поступления в системы вспомогательной сети, как:  или  Следовательно, подставляя данное выражение винвариантное можно определить правила преобразования для вектора загрузки исходной сети через загрузки примитивной или декомпозиционной сети в виде:  Тогда для нахождения правила преобразования для тензора средней длительностей обслуживания, используем уравнение состояния примитивной сети (), из которого получаем, что искомое правило определяется, как:Таким образом, уравнение состояния вспомогательной сети приобретает следующий вид:

                                                         (1)

Решение уравнения (1) относительно контурных интенсивностей () позволит найти распределение трафика в исследуемой спутниковой сети, как:

                                                                      (2)

Так как структура вспомогательной сети совпадает со структурой исходной, то Распределение трафика определяется выражением (2), из которого загрузка для каждой системы может быть найдена, как:  или Нахождение распределения трафика в сети позволяет найти перегруженные участки и разработать методы перенаправления потоков информации для предотвращения перегрузки. Следовательно, разработаннаямодель позволит оценить эффективность работы исследуемой сети с целью повышения ее производительности.

3.      Численные результаты.

Структура модели исследуемой сети формируется в соответствии салгоритмом, представленным в [6], с разделением функций каналов передачи и систем обработки. Таким образом в структуре модели (рис. 3) общее число систем составляет 36, двадцать четыре из которых реальные, а 12 мнимые, описывающие пары источник-получательинформации.

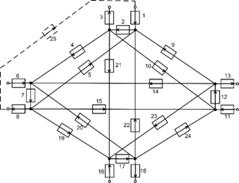
Рис.3. Структура модели исследуемой сети

Пользовательский трафик поступает на спутниковые системы 1,2,3 и 4 (рис. 1) через системы модели 1,6,11 и 16 (рис. 3) соответственно. Каналы передачи между спутниками 1 и 2 моделируются системами 4,5. Аналогичную роль выполняют системы 9,10 (канал спутник 1-спутник 3); 21,22 (канал спутник 1-спутник 4); 14,15 (канал спутник 2-спутник 3); 19,20 (канал спутник 2-спутник 4); 23,24 (канал спутник 3-спутник 4). Мнимые системы формируют замкнутые контуры. В качестве примера мнимой системы приведена система 25, нагрузка которой определяется трафиком между спутниками 1 и 2. В исследуемой сети заданы основные маршруты передачи (номера указывают номер спутника, рис. 1): 1-2, 1-3, 1-4, 2-1, 2-3, 2-4, 3-1, 3-2, 3-4, 4-1, 4-2, 4-3; и обходные: 1-2-4, 1-3-4, 4-3-1, 4-2-1. Таким образом, формируется 16 маршрутов передачи.

В качестве исходных данных выбраны следующие.Длительность обслуживания во всех системах кроме 2,7,12,17 равна 0.01, в указанных системах длительность выбрана значением 0.001, так как это модели высокоскоростных систем обработки на борту. Предварительные интенсивности определяются исходя из требований по недопустимости перегрузки систем и равны 0.3 для всех систем кроме 1,6,11,16 (данные системы являются источниками трафика), для которых выбраны значения: 0.9 для 1 и 6, 1.2 для 11 и 16.

В таком случае, используя информацию об участии отдельных систем в организации пути можно сформировать матрицу перехода  (здесь не приводится в связи с большой размерностью).

Первые три столбца данной матрицы определяются путями от первого спутника ко второму, третьему и четвертому спутникам. Вторые три столбца устанавливаются путями к первому спутнику от второго, третьего и четвертого спутниковых узлов. С седьмого по двенадцатый столбцы связаны с направлениями передачи с третьего и четвертого спутника. Столбцы тринадцатый и четырнадцатый формируют обходные маршруты с первого спутника к четвертому, а пятнадцатый и шестнадцатый столбцы обеспечивают направления передачи трафика по обходным маршрутам в направлении спутник 4-спутник 1. Ненулевые элементы строки соответствуют участию ветви с номером равным номеру строки в организации пути передачи информации.Нижняя часть матрицы связана с мнимыми ветвями, участие которых в топологии определяется путями передачи информации.

Решение уравнения (1) позволило найти контурные интенсивности для данной сети, и использование выражения (2) обеспечило нахождение распределения трафика в исследуемой сети. Полученное распределение обеспечивает для всех систем загрузку, не превышающую единицы. Например, трафик поступающий от пользователей спутника 1 составил 75.375 у.е., который был распределен по ветвям 4, 10 и 21, как 30.128 у.е., 27.186 у.е. и 18.061 у.е.соответственно, что составило загрузку систем 1, 4, 10, 21: 0.754, 0.301, 0.272, 0.181.

Полученные результаты позволяют о возможности применения контурной модели для анализа распределения трафика в перспективных инфокоммуникационных спутниковых сетях с организацией межспутниковых каналов связи.

Заключение

В связи с тем, что в современных и перспективных спутниковых сетях необходимо управлять большим количеством систем при динамическом изменении топологии сети и обеспечивать обработку множества информационных потоков с заданным качеством обслуживания для каждого типа потока, решение задачи управления эффективным использованием ресурсов сети значительно усложняется. Тензорный анализ сетей позволяетучитывать процессно-структурное взаимодействие, проявляющееся в сетях,обладаетвысокой гибкостью применения и обеспечиваетхорошую формализуемость проектных процедур для решения данной задачи, что в свою очередьпозволяет задать требуемый уровень загрузки систем при динамическом управлении инфокоммуникациями и обеспечить хорошую масштабируемость сети как при внедрении новых услуг, так и при изменении структуры и внедрении новых технологий инфокоммуникационной спутниковой сети.

Рецензенты:

Петров М.Н., д.т.н., профессор, ФГБОУ ВПО СибГАУ, г. Красноярск;

Антамошкин А.Н., д.т.н., профессор, профессор кафедрыСАиИОФГБОУ ВПО Сибирского государственного аэрокосмического университета им. акад. М.Ф. Решетнева, г. Красноярск.