Общим для этих задач являются ограниченность ресурсов, на которых обрабатываются заявки (сигналы, детали), и цель– минимизация времени нахождения заявок в системе (время ожидания плюс время обслуживания).
В качестве критерия оперативности обработки заявок в открытой системе обслуживания,как правило,рассматриваетсядоля заявок, время ожидания которых не менее заданного τ [1] .
В настоящей работе исследуется задача распределения ресурсов по указанному критерию для случая, когда интенсивность поступления заявок на вход системы подчиняется детерминированному закону или описывается линейной кусочно-постоянной функцией. Для полученного распределения ресурсов вводится понятие устойчивости решения и анализируется устойчивость в зависимости от изменений интенсивности входного потока.
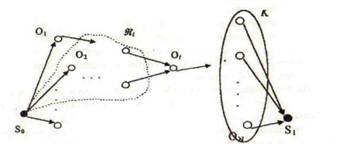
Рис. 1. Граф-структура технологии обработки заявок
Технологию обработки заявок в открытой системе будем представлять ориентированным ациклическим графомG= G(M,N) (рис.1),где:
N– вершины (различные операции обработки заявок);
М – дуги (возможные последовательности обработки заявок на заданном множестве операций) с выделенными вершинами;
![]() –
источник заявок;
–
источник заявок;
![]() –
сток обработанных заявок;
–
сток обработанных заявок;
К – множество конечных (завершающих) операций обработки;
![]() –
множество операций-предшественников для операции
–
множество операций-предшественников для операции ![]() .
.
Фиксируем следующие параметры:
Т – установленный для исследуемой системы временной интервал (мин, час, сутки);
![]() –
(кратное Т) — максимальное время пребывания заявки в очереди;
–
(кратное Т) — максимальное время пребывания заявки в очереди;
![]() –
(кратное Т) — продолжительность периода, на котором распределяются
ресурсы (директивный период).
–
(кратное Т) — продолжительность периода, на котором распределяются
ресурсы (директивный период).
Пусть интенсивность поступления заявок со временем
ожидания не менее ![]() на
операцию с номером i
в интервале
на
операцию с номером i
в интервале ![]() задается
величиной
задается
величиной ![]() . Очереди на
каждой операции на начало директивного периода задаются величинами
. Очереди на
каждой операции на начало директивного периода задаются величинами![]() (объем очереди на операции i, со временем ожидания
заявок не менее
(объем очереди на операции i, со временем ожидания
заявок не менее ![]() ).
).
Выполнение обработки операций технологического цикла
осуществляется на Рединицах оборудования, производительности которых задаются
матрицей ![]() размерности NxP, где
размерности NxP, где![]() – производительность
p-го
оборудования на i-й
операции (
– производительность
p-го
оборудования на i-й
операции (![]() в случае,
если i-я
операция наp-м
оборудовании не осуществляется).
в случае,
если i-я
операция наp-м
оборудовании не осуществляется).
Необходимо организовать обработку поступающих заявок
таким образом, чтобы на конец периода продолжительностью ![]() минимизировать в очереди объем заявок
со временем ожидания не менее
минимизировать в очереди объем заявок
со временем ожидания не менее![]() .
.
Поиск оптимального распределения ресурсов будем осуществлять в предположении, что заявки с операции на операцию передаются мгновенно (без учета «транспортного» лага). Последнее условие накладывает существенные ограничения на исследуемую модель, не искажая, тем не менее, качественной картины.
В такой постановке задача может быть сведена к задаче
распределения ресурсов по критерию максимизации общего объема обработанных за
директивный период заявок. Для этого достаточно рассмотреть среди всех заявок,
находящихся в очередях ![]() , и среди заявок,
поступающих на обработку
, и среди заявок,
поступающих на обработку ![]() . «Возраст»
. «Возраст»
![]() которых к окончанию
периода [0,
которых к окончанию
периода [0,![]() ] будет не
менее
] будет не
менее ![]() .
.
Исходя из этого положения примем в качестве входного потока заявок следующий:
![]() (1)
(1)
Объемы очередей на операциях в начале директивного периода рассчитаем по формуле:
![]() (2)
(2)
Обозначим![]() - частьj-го интервала, в течение
которого р-еоборудование выполняетi-ю операцию.
- частьj-го интервала, в течение
которого р-еоборудование выполняетi-ю операцию.
Задача минимизации объемов необработанных заявок со
временем ожидания к концу директивного периода не менее т может быть сформулирована как следующая
оптимизационная (относительно ![]() ) задача:
) задача:
![]() (3)
(3)
при ограничениях
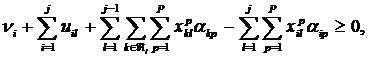 (4)
(4)
i=1,…,N; j=1,…,![]() (условие баланса очередей);
(условие баланса очередей);
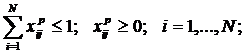 (5)
(5)
j=1,…,![]() ;
p=1,…,P(условие баланса
оборудования).
;
p=1,…,P(условие баланса
оборудования).
Задача (3)—(5), учитывая линейность функционала и ограничений, относится к задачам линейного программирования (ЛП).
Рассмотрим, как изменяется значение функционала(3) при
изменении интенсивности![]() потока
входных заявок.
потока
входных заявок.
Фиксируем целое ![]() , большее 0.
, большее 0.
Определение 1.
Задача (3)—(5) ![]() –
устойчива по интенсивности поступления заявок
–
устойчива по интенсивности поступления заявок ![]() , если для всех точек
, если для всех точек ![]() окрестности (
окрестности (![]() ,
,![]()
![]()
![]() )значение функционала (1) остается неизменным.
)значение функционала (1) остается неизменным.
Определение 2.
Максимальное![]() , при
котором задача (3)—(5)
, при
котором задача (3)—(5) ![]() —
устойчива по интенсивности поступления заявок, назовем радиусом устойчивости
задачи по интенсивности входного потока заявок.
—
устойчива по интенсивности поступления заявок, назовем радиусом устойчивости
задачи по интенсивности входного потока заявок.
Пусть![]() – решение задачи (3)-(5) и
значение функционала (3) прираспределения
– решение задачи (3)-(5) и
значение функционала (3) прираспределения![]() равно
равно ![]() . Определить диапазон изменения
интенсивности входного потока заявок можно, решив следующие задачи ЛП относительно
. Определить диапазон изменения
интенсивности входного потока заявок можно, решив следующие задачи ЛП относительно
![]() и
и ![]() :
:
![]() ; (6)
; (6)
![]() (7)
(7)
![]() (8)
(8)
i=1,…,N; j=1,…,![]() ;
;
![]() (9)
(9)
j=1,…,![]() ; p=1,…,P.
; p=1,…,P.
![]() ; (10)
; (10)
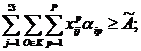 (11)
(11)
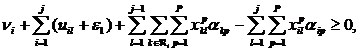 (12)
(12)
i=1,…,N; j=1,…,![]() ;
;
![]() (13)
(13)
j=1,…,![]() ; p=1,…,P.
; p=1,…,P.
Радиус ![]() устойчивости исходной
задачи (3)-(5) по интенсивности входного потока заявок определим по формуле:
устойчивости исходной
задачи (3)-(5) по интенсивности входного потока заявок определим по формуле:
![]()
Рассмотрим случай, когда интенсивности поступления
заявок на обработку заданы кусочно-постоянными функциями. Разобьем директивный
период на интервалы ![]() ,
на каждом из которых интенсивность
,
на каждом из которых интенсивность ![]() поступления
заявок на каждую операцию постоянна.
поступления
заявок на каждую операцию постоянна.
Задачу оптимального распределения ресурсов будем
рассматривать для каждого интервала ![]() :
:
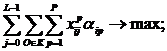 (15)
(15)
![]() (16)
(16)
i=1,…,N; j=0,…,L-1;
![]() (17)
(17)
j=0,…,L-1; p=1,…,P.
Примечание.![]() – часть интервала
– часть интервала ![]() , на котором p-еоборудование используется на i-й операции;
, на котором p-еоборудование используется на i-й операции; ![]() – объем
очереди на i-й
операции в начале интервала
– объем
очереди на i-й
операции в начале интервала ![]() .
.
В случаеесли производительности каждой из Pединиц оборудования на рассматриваемом интервале не превышают интенсивностей поступления заявок, решение задачи (15)—(17) дает оптимальное по производительности распределение оборудования.
Обратно, если производительность каждой единицы
оборудования на рассматриваемом интервале ![]() превышает интенсивность
поступления заявок, то, разрешив кольцевую процедуру переключения оборудования
с одной операции на другую [5], можно сохранить распределение соответствующей
ЛП-задачи и обработанный объем заявок сделать сколь угодно близким к значению Афункционала
(13). Докажем этот факт. Выберем
превышает интенсивность
поступления заявок, то, разрешив кольцевую процедуру переключения оборудования
с одной операции на другую [5], можно сохранить распределение соответствующей
ЛП-задачи и обработанный объем заявок сделать сколь угодно близким к значению Афункционала
(13). Докажем этот факт. Выберем ![]() .Для того, чтобы получить распределение
оборудования по операциям на интервале
.Для того, чтобы получить распределение
оборудования по операциям на интервале ![]() ,которое даст объем
обработанных заявок
,которое даст объем
обработанных заявок ![]() , поступим
следующим образом. Разобьем интервал
, поступим
следующим образом. Разобьем интервал ![]() на подинтервалы длиной
на подинтервалы длиной ![]() и на каждом из
подинтервалов сохраним распределение, полученное в задаче (15)—(17), сократив
время работы каждой единицы оборудования в
и на каждом из
подинтервалов сохраним распределение, полученное в задаче (15)—(17), сократив
время работы каждой единицы оборудования в![]() раз. Вэтом случае
производительность оборудования на каждом из полученных подинтервалов (за
исключением, быть мажет, первого) будет равна
раз. Вэтом случае
производительность оборудования на каждом из полученных подинтервалов (за
исключением, быть мажет, первого) будет равна ![]() , что и доказывает сформулированное
утверждение.
, что и доказывает сформулированное
утверждение.
Для задачи (15)—(17) можно рассматривать обобщенный
критерий оперативности обработки поступающих заявок: насколько велико максимальное
время ожидания заявок в системе. В этом случае для получения оптимального
распределения может быть применена процедура итерационного решения задачи (15)—(17)
при различных интенсивностях входного потока заявок, связанных с выбором ![]() времени
ожидания, по которому производится максимизация обработанного объема заявок.
времени
ожидания, по которому производится максимизация обработанного объема заявок.
Загородников С.Н., д.б.н., профессор, профессор кафедры «Математические методы в экономике» ФГБОУ ВПО «Российский экономический университет имени Г.В. Плеханова», г.Москва;
Титов В.А., д.э.н., профессор кафедры «Информационные технологии» ФГБОУ ВПО «Российский экономический университет имени Г.В. Плеханова», г.Москва.
Библиографическая ссылка
Максимов Д.А., Халиков М.А. ОБ ОДНОМ ПОДХОДЕ К РАСПРЕДЕЛЕНИЮ РЕСУРСОВ, МИНИМИЗИРУЮЩЕМ ОБЪЕМ ЗАЯВОК С ЗАДАННЫМ ВРЕМЕНЕМ ОЖИДАНИЯ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18399 (дата обращения: 27.02.2026).



