Рассмотрим, как сказывается ограниченная производительность бортового вычислителя на точность навигационного обеспечения (НО) при использовании более совершенных по сравнению с методом наименьших квадратов (МНК) оптимальных алгоритмов фильтрации навигационных параметоров (НП). Наиболее совершенен метод оптимальной нелинейной фильтрации (ОНФ), позволяющий учитывать наряду с характеристиками шумов измерения, динамикой движения ВС и геометрией рабочего созвездия ВС нелинейность уравнения наблюдения. Полученные на основе методики ОНФ в гауссовом приближении и дискретном времени уравнения для вектора оценок НП и матричного коэффициента передачи фильтра имеют вид [4]:
![]() , (1)
, (1)
![]() . (2),
. (2),
где F - переходная матрица, характеризующая динамику движения ВС; Q - корреляционная матрица динамических шумов; R - корреляционная матрица шумов измерения РНП; H - матрица направляющих косинусов, характеризующая геометрию рабочего созвездия НКА.
При ![]() , (3)
, (3)
где P - корреляционная матрица ошибок оценки НП, уравнения (1) и (2) совпадают с уравнениями многомерной оптимальной линейной фильтрации (ОЛФ) - фильтрации Калмана, которые в случае фильтрации установившегося процесса, то есть, когда элементы матрицы Н меняются медленно, а динамические свойства ВС не меняются во времени (элементы матрицы Q постоянны) записываются [1]:
![]() , (4)
, (4)
![]() . (5)
. (5)
Как показано в [5], при не сильно выраженной нелинейности уравнения наблюдения, что в рассматриваемом случае обусловлено большими значениями дальностей от ВС до НКА, позволяющими использовать линеаризованную матрицу Н, ОЛФ обеспечивает результаты, близкие к результатам, получаемым при использовании ОНФ, будучи при этом более простой в реализации.
Как видно из (4) и (5), алгоритм ОЛФ имеет рекуррентную форму. При этом корреляционная матрица ошибок фильтрации Р в отличие от случая МНК не может быть вычислена аналитически, так как нелинейное матричное уравнение Риккати (5) не имеет аналитического решения. Это создает определенные трудности при построении рабочих алгоритмов ОЛФ в случае большой размерности фильтра п, поскольку объем вычислений Р растет, как показывает анализ, пропорционально п3.
Промежуточное положение между МНК и ОЛФ занимает квазиоптимальная линейная фильтрация (КЛФ), при которой в каждом канале измерения псевдодальности и псевдоскорости применяется ОЛФ второго порядка. Затем результаты фильтрации обрабатываются с помощью МНК. При этом КЛФ требует меньшей затраты вычислительных средств по сравнению с многомерной ОЛФ.
Чтобы вычислить корреляционную матрицу ошибок Р фильтрации НП l* сначала нужно для каждого к-го канала измерений вычислить матрицу Рк оценок вектора [rк Vк]Т. Уравнения состояния и наблюдения в данном случае перепишутся в виде [2]:
![]() , к = 1, 2, ..., т , (6)
, к = 1, 2, ..., т , (6)
![]() , к = 1, 2, ..., т . (7)
, к = 1, 2, ..., т . (7)
Здесь векторные случайные процессы пк и пок представляют собой соответствующие составляющие векторов п и по, а их корреляционные матрицы Qк и Rк равны соответствующим блокам размерностью 2 ґ 2 матриц Q и R. При этом, полагая, что ВС одинаково подвижен во всех направлениях, а измерения в каналах равноточные, можем записать:
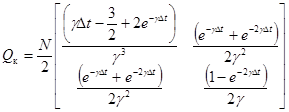 , (8)
, (8)
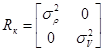 , (9)
, (9) 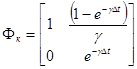 . (10)
. (10)
С учетом (5) и (8) - (10) для ОЛФ 2-го порядка в каждом из каналов измерений можно записать:
![]() , (11)
, (11)
![]() . (12)
. (12)
Если ограничиться оценкой точности определения координат ВС, то матрица ошибок фильтрации псевдодальностей на входе блока обработки по МНК, Рвх будет иметь вид диагональной матрицы с элементами в главной диагонали: Р1, Р2, Р3, Р4.
После обработки по МНК предварительно отфильтрованных результатов измерения РНП r* на выходе КЛФ получится оценка вектора НП l*, которая будет иметь вид [3]:
![]() , (13)
, (13) ![]() . (14)
. (14)
НП целесообразно использовать лишь при высокой производительности вычислителя, обеспечивающей обработку навигационной информации при малом шаге дискретизации. При этом выигрыш в точности от их применения по сравнению с МНК существенен (примерно на порядок).
При низкой производительности вычислителя использование ОЛФ нецелесообразно, поскольку она обеспечивает точность фильтрации НП, близкую к точности, реализуемой при существенно более простом алгоритме МНК. Тем более нецелесообразно использование в этом случае КЛФ, обеспечивающей точность худшую, чем при использовании МНК.
При размещении АП СРНС на ВС существенное влияние на его точностные характеристики оказывают динамические характеристики ВС, а именно: интенсивность, характеризуемая величиной среднеквадратического отклонения скорости от ее среднего значения sVВС, и эффективная ширина спектра флуктуаций скорости ВС g.
Оценим степень влияния динамики движения ВС на точностные характеристики размещаемой на нем АП СРНС при различных рассмотренных выше алгоритмах фильтрации НП. Такое рассмотрение проведем применительно к задаче определения координат ВС.
При этом в качестве величины, характеризующей точность определения координат ВС, будем использовать радиальную СКО местоопределения ВС sr = (Pxx + Pyy + +Pzz)1/2, где Pxx , Pyy и Pzz - элементы корреляционной матрицы Р ошибок оценок вектора НП, равные дисперсиям по каждой из декартовых координат ВС x, y и z .
Анализ проведем при различных значениях ГФ ошибки трехмерного местоопределения ВС:
Гr = [Tr(GGT)]1/2 = ![]() , (15)
, (15)
позволяющего учесть влияние на точность местоопределения ВС расположения НКА рабочего созвездия. Здесь Tr - след матрицы (сумма диагональных элементов), а sr - СКО оценки РНП.
Для простоты будем, как и ранее, полагать измерения РНП в каналах равноточными. При этом в рамках марковской модели движения ВС, положенной в основу уравнения состояния, автокорреляционная функция (АКФ) флуктуаций скорости ВС по каждой из координат имеет вид [3]:
К(t) = s2VВС е-gзt з, (16)
где sVВС - среднеквадратическое отклонение флуктуаций скорости ВС, характеризующее интенсивность флуктуаций, связанное с их односторонней спектральной плотностью N и эффективной шириной спектра флуктуаций скорости g, которая обратно пропорциональная интервалу корреляции флуктуаций tк.
Для практических приложений представляет интерес оценка влияния параметров sVВС и g, характеризующих динамические свойства ВС, на точность определения его координат при различных значениях шага дискретизации Dt, выбираемого, исходя из производительности вычислителя, используемого для реализации рассматриваемых алгоритмов фильтрации НП.
Такой подход позволит оценить влияние динамических воздействий на точность определения координат подвижного объекта при различных алгоритмах фильтрации с учетом требований к производительности вычислителя, используемого для реализации этих алгоритмов.
Из кривых на рисунках 1 и 2 видно, что увеличение g влияет на точность местоопределения ВС качественно также, как и увеличение sVВС, а именно: с увеличением g ошибка увеличивается, выигрыш в точности при использовании ОЛФ и КЛФ по сравнению с МНК уменьшается и область значений Dt, при которых этот выигрыш наблюдается, сужается. Однако чувствительность ошибки местоопределения к изменению g меньше, чем к изменению sVВС. Это может быть объяснено тем, что при достаточно больших значениях Dt ошибка при использовании ОЛФ и КЛФ приближается к ошибке при МНК, определяемой выражением:
srMНК = [(Гr sr)2 + NDt 3/2]1/2 , (17)
откуда для N следует, что динамическая составляющая ошибки, связанная с флуктуациями скорости ВС, равна:
srMНК(дин.) = (N/2)1/2 Dt 3/2 = (2g)1/2sVВСDt 3/2. (18)
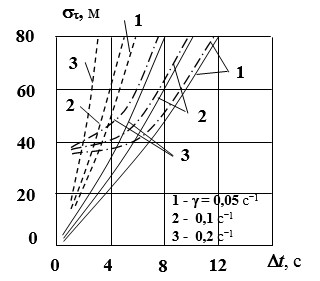
Рис. 1. Зависимость радиальной ошибки местоопределения ВС от шага дискретизаций измерений и ширины спектра флуктуаций скорости ВС дальномерным методом
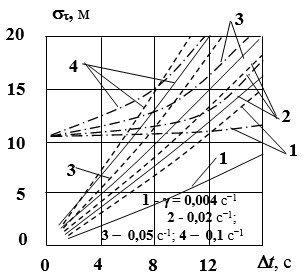
Рис. 2. Зависимость радиальной ошибки местоопределения ВС от шага дискретизаций измерений и ширины спектра флуктуаций скорости ВС псевдодальномерным методом с использованием МНК, ОЛФ и КЛФ
Как видим, эта составляющая ошибки пропорциональна среднеквадратическому отклонению флуктуаций скорости ВС и корню квадратному из эффективной ширины спектра этих флуктуаций, то есть ошибка более чувствительна к изменению sVВС, чем к изменению g.
Таким образом, проведенное рассмотрение показало, что условия эксплуатации АП СРНС, размещаемой на ВС, а именно: интенсивность и ширина спектра флуктуаций его скорости оказывают значительное влияние на точность определения координат ВС.
При этом интенсивность флуктуаций оказывает большее влияние по сравнению с шириной их спектра. Выигрыш в точности за счет использования ОЛФ и КЛФ по сравнению со случаем использования МНК уменьшается при увеличении динамических воздействий на ВС, оставаясь достаточно высоким (уменьшение СКО в 2-6 раз).
Вместе с тем, поскольку область значений шага дискретизации, используемой при цифровых методах фильтрации, в пределах которой обеспечивается выигрыш в точности за счет использования ОЛФ и КЛФ, при увеличении интенсивности и ширины спектра флуктуаций скорости ВС сужается, требования к производительности бортового вычислителя при работе АП СРНС в условиях интенсивных динамических воздействий на ВС, в частности вызываемых атмосферными возмущениями, ужесточаются.
Использование ОЛФ и КЛФ для фильтрации НП, снижая требования к производительности бортового вычислителя (при сохранении требований к точности НО), с другой стороны, ужесточает эти требования за счет усложнения алгоритма фильтрации. Снизить объем вычислений, необходимый для осуществления фильтрации НП, позволяет алгоритм подоптимальный линейной фильтрации (ПЛФ).
При использовании этого алгоритма матрицы Ф, Q, R, Н в нелинейном матричном уравнении Риккати (5), на решение которого тратится большая часть вычислительного ресурса при ОЛФ, в выражении для матричного коэффициента усиления алгоритма оценки вектора состояния ВС (4):
K = (P-1 + HT R-1 H)-1 HT R-1 (19)
на каждом шаге фильтрации принимаются постоянными, и вместо рекуррентных вычислений по формулам (5) и (4) производится только вычисление оценки вектора состояния ВС по формуле:
![]() . (20)
. (20)
При этом К вычисляется путем решения уравнения Риккати (5) раз в несколько минут одновременно с выбором рабочего созвездия.
К преимуществам ПЛФ относится существенное сокращение объема вычислений за счет того, что в ритме выдачи НП вычисления необходимо проводить только по формуле (20), а остальные вычисления могут проводиться раз в 3-6 мин. ПЛФ не уступает в точности ОЛФ, если на интервале между двумя последовательными вычислениями Р и К матрицы Ф, Q, R, то есть динамические характеристики движения ВС и статистические характеристики шумов измерений, изменяются незначительно.
Элементы матрицы Н изменяются медленно, поэтому их изменением при работе по одному и тому же рабочему созвездию НКА можно пренебречь. Однако при смене рабочего созвездия значения элементов Н меняются скачком, поэтому во время переходного процесса после смены рабочего созвездия ПЛФ может существенно уступать в точности ОЛФ.
Для оценки этого эффекта проводилось статистическое моделирование работы многомерного ОЛФ, работа которого задается уравнениями (4) и (5).
Моделирование работы ПЛФ, работа которого задается уравнением (20) и формулой (19), проводилось при тех же начальных значениях матриц Ф, Q, R и Н, что и моделирование работы ОЛФ.
Моделирование проводилось для трехмерного местоопределения по трем НКА дальномерным методом. Результаты показали, что в течение переходного процесса, длительность которого может достигать 50 с, ошибка ПЛФ может превышать ошибку ОЛФ в 1,5-2 раза. Один из примеров результатов моделирования приведен на рисунке 3.
При моделировании использовались следующие исходные данные: СКО ошибки измерения псевдодальносги sr = 6 м, СКО ошибки измерения псевдоскорости sV = 0,25 м/с, параметры динамической модели ВС - sVВС =2 м/с, g = 0,02 с-1 , период дискретизации фильтра Т = I с.
На рис. 3 приведены кривые для различных значений начального рассогласования фильтра. Пунктирной линией на графике показана ошибка ОЛФ, сплошной - ошибка ПЛФ.
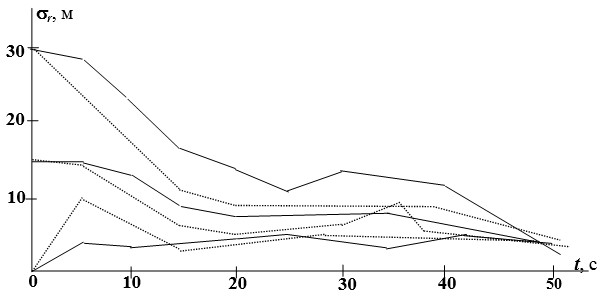
Рис. 3. Переходной процесс после смены рабочего созвездия НКА при
навигационных определениях дальномерным методом с использованием оптимального и подоптимального линейных фильтров
Если ухудшение точности фильтрации после перехода на новое рабочее созвездие по условиям решения НЗ недопустимо, для вычисления матрицы Р во время переходного процесса в ПЛФ может использоваться рекурентный алгоритм, описываемый уравнением Риккати (5).
Рецензенты:
Козлов А.И., д.ф.-м.н., профессор, профессор кафедры «Технической эксплуатации радиоэлектронного оборудования воздушного транспорта» Московского государственного технического университета гражданской авиации, г. Москва;
Акиншин Р.Н., д.т.н., доцент, ведущий научный сотрудник секции по оборонным проблемам Министерства обороны (при Президиуме Российской академии наук), г. Москва.
Библиографическая ссылка
Евтушенко О.А. УМЕНЬШЕНИЕ ВЛИЯНИЯ ОГРАНИЧЕННОЙ ПРОИЗВОДИТЕЛЬНОСТИ БОРТОВОГО ВЫЧИСЛИТЕЛЯ И ДИНАМИКИ ДВИЖЕНИЯ ВОЗДУШНОГО СУДНА НА КАЧЕСТВО ФУНКЦИОНИРОВАНИЯ АППАРАТУРЫ ПОТРЕБИТЕЛЕЙ СПУТНИКОВЫХ РАДИОНАВИГАЦИОННЫХ СИСТЕМ ПУТЕМ СОВЕРШЕНСТВОВАНИЯ АЛГОРИТМА ФИЛЬТРАЦИИ НАВИГАЦИО // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18262 (дата обращения: 12.03.2026).



