Одной из ключевых дисциплин технического образования является «Сопротивление
материалов», изложение которой «в современном понимании в основном сложилось к концу XIX – началу XX века как результат совместных усилий ученых и инженеров ведущих мировых держав. Здесь нельзя не отметить заслуг российской школы механики» [5, с. 6].
В настоящее время в результате эволюции численных методов с точки зрения точности вычислений, адаптации к вычислительной технике, многообразия и сложности решаемых задач, приближения расчетных схем к реальному объекту наибольшее применение получил метод конечных элементов (МКЭ), на основании которого создано много систем КЭ-анализа с высокоразвитым интерфейсом, применяемых в инженерной деятельности.
Таким образом, сложилась парадоксальная ситуация, когда традиционное изложение курса «Сопротивление материалов», основанное на «ручном» выполнении расчетов, вошло в противоречие с требованиями времени. Отсюда проистекает необходимость адаптации студентов к современным вычислительным технологиям на базе МКЭ в области расчетов конструкций на прочность и жесткость.
Как на смену пленки в кинематографе, аналогового сигнала в телевидении приходят цифровые технологии, так и в расчетах напряженно-деформированного состояния инженерных сооружений на смену аналитическим зависимостям приходят численные методы.
Традиционный курс «Сопротивление материалов» рассчитан на подготовку пользователей расчетных формул в области расчета на прочность и жесткость простейших конструктивных элементов инженерных сооружений. Первые попытки применения МКЭ в сопротивлении материалов, предпринятые более 20 лет тому назад [1, с. 550], не имели успеха, т.к. требовали знания и умения программировать на том или ином алгоритмическом языке, что требовало огромных трудозатрат при решении даже простейших задач.
Аналогичная ситуация имеет место и в преподавании графических дисциплин [6], где, наряду с традиционным «ручным» графическим моделированием объекта, применяется конечно-элементная система автоматизированного проектирования SolidWorks COSMOSWorks, позволяющей выполнять прочностной и жесткостной анализы.
Цель настоящей статьи состоит в демонстрации возможности применения конечно-элементного анализа в преподавании дисциплины «Сопротивление материалов» наряду с традиционной формой изложения, показать, какая основная информация циркулирует в системах КЭ-анализа, а также адаптировать студентов к интерфейсу выбранного КЭ-пакета.
Наиболее просто в конечно-элементном изложении рассматривается плоская задача теории упругости, визуализация которой дает студенту наиболее полное представление о сущности рассматриваемых задач в сопротивлении материалов.
Традиционно в сопротивлении материалов привыкли определять напряжения и деформации для бруса, для которого справедлива гипотеза плоских сечений и на брусе отрабатывалась технология анализа напряженно-деформированного состояния.
Конечно-элементное моделирование не использует гипотезу плоских сечений, но наглядно демонстрирует студентам возможность ее применения при использовании балочной технологии (рис. 1, 2).
Современные вычислительные технологии предлагают другую методику определения напряженно-деформированного состояния конструкции, основанную на расчленении конструкции на отдельные области, в которых справедливы соотношения сопротивления материалов. В принципе, в традиционном сопротивлении материалов эта методика и применяется, рассматривая конструкцию по участкам.
Студентам на примере балки-стенки, испытывающей плоское напряженное состояние, показывается сущность МКЭ, рассматривая основные этапы его приложения для создания интуитивно-понятийных представлений. Причем все построено на основных понятиях традиционного курса сопротивления материалов.
Этап 1. Построение дискретной модели пластины. Демонстрируется ручная процедура построения геометрической информации дискретной модели, основой которой является матрица геометрии конструкции, содержащая координаты узлов, и матрица топологии конструкции, показывающая, какой конечный элемент какие узлы соединяет. По информации, заданной в этих матрицах, можно в цикле по числу узлов и в цикле по числу элементов построить изображение дискретной модели пластины на экране или вручную на бумаге. В системах КЭ-анализа конструкция вычерчивается с помощью средств машинной графики, по параметрам, устанавливаемым пользователем, т.е. графическим препроцессором.
Этап 2. Процедура построения зависимостей, характеризующих упругие свойства треугольного плоского конечного элемента (вывод матрицы жесткости КЭ) в терминах и определениях традиционного курса сопротивления материалов.
На выделенный е-ый треугольный элемент будут действовать внешние узловые усилия ![]() , под действием которых элемент деформируется, его текущая точка получит перемещения
, под действием которых элемент деформируется, его текущая точка получит перемещения ![]() вдоль осей
вдоль осей ![]() и
и ![]() соответственно. При этом узлы элемента приобретут перемещения
соответственно. При этом узлы элемента приобретут перемещения ![]() , на которых внешние по отношению к элементу узловые усилия
, на которых внешние по отношению к элементу узловые усилия ![]() совершат работу
совершат работу ![]() Здесь множитель 0,5 обусловлен тем, что узловые усилия
Здесь множитель 0,5 обусловлен тем, что узловые усилия ![]() и соответствующие им узловые перемещения
и соответствующие им узловые перемещения ![]() связаны между собой законом Гука.
связаны между собой законом Гука.
Аппроксимируем перемещения по плоскости конечного элемента полиномом вида
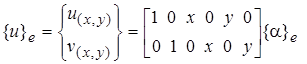 или
или ![]() , (1)
, (1)
где ![]() вектор неизвестных пока коэффициентов, число которых равно числу узловых перемещений (усилий) выделенного конечного элемента. Расположение коэффициентов может быть произвольным, поэтому, чтобы иметь сравнение выбран вариант, который применен в работе [3, с. 159].
вектор неизвестных пока коэффициентов, число которых равно числу узловых перемещений (усилий) выделенного конечного элемента. Расположение коэффициентов может быть произвольным, поэтому, чтобы иметь сравнение выбран вариант, который применен в работе [3, с. 159].
Подставляя в выражение (1) координаты узлов выделенного конечного элемента, можно выразить вектор ![]() через вектор узловых перемещений
через вектор узловых перемещений
![]() , (2)
, (2)
где ![]() – матрица координат узлов выделенного конечного элемента.
– матрица координат узлов выделенного конечного элемента.
Отсюда
![]()
![]() , (3)
, (3)
подставляя которое в (1), получим
![]() . (4)
. (4)
Ценность выражения (4) состоит в том, что перемещения точек выделенного КЭ полностью определяются его узловыми перемещениями.
Деформированное состояние КЭ определим, воспользовавшись зависимостями Коши, также рассматриваемыми в традиционном курсе сопротивления материалов [6, с. 276]
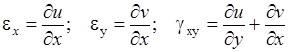 , (5)
, (5)
подстановка в которые выражения (1) дает
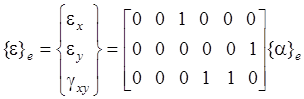 или
или ![]() . (6)
. (6)
Подставив выражение (3) в (6), получим деформированное состояние в текущей точке элемента, полностью определяемое его узловыми перемещениями
![]() . (7)
. (7)
Напряженное состояние КЭ определим, воспользовавшись законом Гука для плоского напряженного состояния [5, с. 112].
![]()
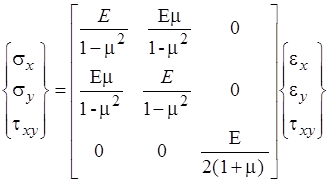 или
или ![]() . (8)
. (8)
Подставив выражение (7) в зависимость (8), получим напряженное состояние в текущей точке КЭ, полностью определяемое его узловыми перемещениями
![]() . (9)
. (9)
Потенциальная энергия деформации выделенного КЭ определяется как
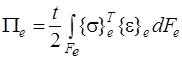 , (10)
, (10)
где t – толщина, ![]() – площадь треугольного конечного элемента, выраженная через координаты его узлов.
– площадь треугольного конечного элемента, выраженная через координаты его узлов.
После подстановки выражений (9) и (7) в (11) будем иметь
![]() , (11)
, (11)
где ![]() – симметричная матрица жесткости плоского треугольного конечного элемента.
– симметричная матрица жесткости плоского треугольного конечного элемента.
Закон сохранения энергии, согласно которому работа внешних узловых сил, приложенных к конечному элементу, равна потенциальной энергии деформации этого элемента, принимает вид
![]() . (12)
. (12)
Отсюда получаем основное соотношение МКЭ, устанавливающее связь между узловыми усилиями конечного элемента и его узловыми перемещениями
![]() (13)
(13)
Определять развернутые выражения коэффициентов матрицы жесткости ![]() , имеющей размер 6˟6, в учебном процессе нет необходимости, так как числовые значения автоматически получаются после перемножения матриц.
, имеющей размер 6˟6, в учебном процессе нет необходимости, так как числовые значения автоматически получаются после перемножения матриц.
Такой же ход рассуждений демонстрируется студентам и при выводе матрицы жесткости объемного конечного элемента (SOLID).
Примером изложенного выше подхода при выводе выражения (13) может служить общепринятая в сопротивлении материалов методика определения осадки пружины с небольшим шагом витка [1, с. 506].
Студентам поясняется, что по аналогичному сценарию можно построить матрицы жесткости различных конечных элементов (балочных, оболочечных и др.), создать каталог конечных элементов, что и сделано в различных системах конечно-элементного анализа (ANSYS, COSMOS, NASTRAN и др.).
Вывод матрицы жесткости и эквивалентной нагрузки балочного элемента (BEAM2D) производится исходя из дифференциального уравнения изгиба бруса, загруженного равномерно-распределенной нагрузкой.
Этап 3. Построение системы алгебраических уравнений всей конструкции из ансамбля конечных элементов ее составляющих производится из условия равновесия ее узлов, согласно которому внешняя нагрузка, действующая на узел, уравновесится упругими усилиями взаимодействия узла со сходящимися в нем элементами. Реакция каждого элемента на перемещения его узлов определяется его матрицей жесткости [K]е. Рассматривая равновесие каждого узла по двум направлениям, получим необходимое число уравнений для определения перемещений всех узлов балки-стенки.
Ручная процедура рассмотрения равновесия каждого узла с учетом сходящихся в нем конечных элементов очень трудоемка и требует повышенного внимания, однако она легко алгоритмизируется с помощью матрицы (строки) индексов, сопоставляющей нумерацию перемещений рассматриваемого конечного элемента с нумерацией перемещений во всей конструкции. По строке индексов и производится рассылка содержимого матрицы жесткости конечного элемента по полю глобальной матрицы жесткости всей конструкции. Подобная процедура автоматически осуществляется в системах конечно-элементного анализа. В результате получаем матричное уравнение
[K]{q}={Q}, (14)
где [K] – глобальная матрица жесткости всей конструкции (балки-стенки); {q} – глобальный вектор перемещений всех узлов конструкции; {Q} – глобальный вектор узловой нагрузки, действующей на конструкцию. Студентам на примере балки-стенки демонстрируется процедура формирования глобальной матрицы жесткости.
Этап 4. Решение системы уравнений (14). Глобальная матрица жесткости [K] симметрична относительно главной диагонали и имеет ленточную структуру. Поэтому для решения матричного уравнения (14) разработаны специальные алгоритмы, позволяющие определить глобальный вектор перемещений {q}, наложив которые в определенном масштабе на геометрию дискретной модели, можно построить деформированный вид конструкции, что и делается в системах конечно-элементного анализа с помощью графического постпроцессора.
Этап 5. Определение напряжений (в том числе главных) и деформаций внутри каждого конечного элемента. Зная перемещения узлов каждого конечного элемента (их можно выбрать из глобального вектора перемещений {q} с помощью индекс-строки рассматриваемого конечного элемента), можно определить напряжения (9) и деформации (7) по полю каждого конечного элемента. В результате с помощью графического постпроцессора в цветах строятся напряженное и деформированное состояния конструкции.
Полный цикл задач, выполняемых в курсе сопротивления материалов с применением КЭ-анализа, приведен в работе [2]. На рис.1 демонстрируется один из примеров расчета студентами балки-стенки при использовании балочных элементов (BEAM2D) и элементов, моделирующих плоскую задачу теории упругости, рассмотренную ранее по формулам (1÷13), (элементы PLANE2D). Хорошо просматривается гипотеза плоских сечений, на которой в основном базируется традиционный курс сопротивления материалов.
а) 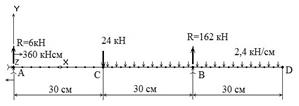 б)
б) 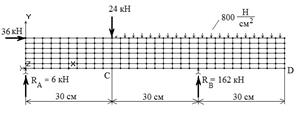
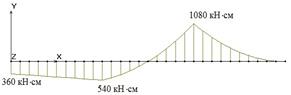
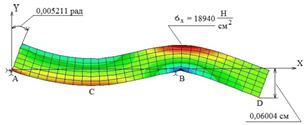

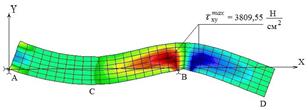
Рис. 1. Напряженно-деформированное состояние балки-стенки:
а) полученное по балочной технологии (BEAM2D); б) полученное по технологии плоской задачи теории упругости (PLANE2D)
Напряженно-деформированное состояние при объемном моделировании (SOLID) (рис. 2) демонстрирует максимальную близость расчетной схемы к реальному объекту.
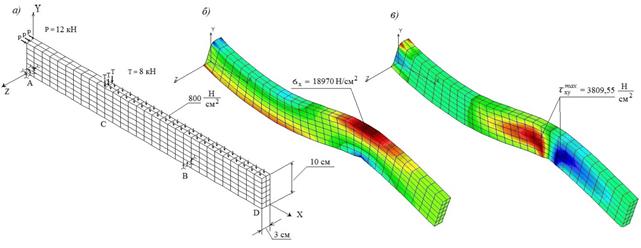
Рис. 2. Напряженно-деформированное состояние балки-стенки, полученное по технологии объемной задачи теории упругости (SOLID): а) нагружение бруса; б) распределение нормальных напряжений; в) распределение касательных напряжений
Расчеты, выполненные по трем расчетным схемам (BEAM2D, PLANE2D, SOLID) одного и того же бруса, и сравнение их с ручным счетом демонстрируют студентам различные подходы, вычислительные возможности и дают более полное представление об объекте, особенно в режиме анимации.
По результатам, полученным в сопротивлении материалов на основании МКЭ, легко перейти к строительной механике, теории колебаний упругих систем и другим дисциплинам, касающихся механики деформированного твердого тела. В качестве примера, выполняемого студентами, на рис. 3 показано напряженно-деформированное состояние рамы, сначала загруженной статической нагрузкой, а затем испытывающей мгновенное снятие нагрузки (динамический процесс). Вариант задания взят из работы [4, с.141]. Рама выполнена из стального двутавра № 10 (Jz=198 см4, А=12 см2).
Динамический расчет выполнялся следующим образом:
1. Дополнительно вводились ρ=7850 кг/м3 – массовая плотность материала, DEMP = 0,03 – коэффициент демпфирования;
2. Определялись 5 собственных частот колебаний рамы (λ1 = 23,83 Гц, λ2 = 66,69 Гц и др.);
3. Исходя из заданного для наблюдения частотного интервала в 200 Гц, по теореме Котельникова подсчитывался максимально достаточный временной шаг интегрирования Δt ≤ 0,0025 сек и по нему принимался шаг Δt = 0,0015 сек;
4. Медленное динамическое нагружение рамы во времени и затем мгновенное снятие всей нагрузки. Процедура медленности определялась периодом собственных колебаний рамы первого тона, т.е. время нагружения было принято равным 1/λ1 = 0,042 сек. Число шагов принималось равным 1000, поэтому колебания рамы наблюдались во временном интервале от 0 до 1,25 сек;
5. Расчет спектра горизонтальных колебаний 55-го узла рамы.
Статическое нагружение рамы
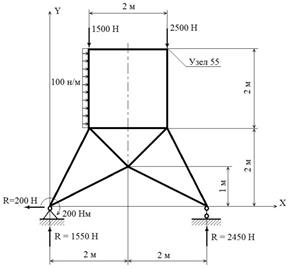
Деформированный вид рамы
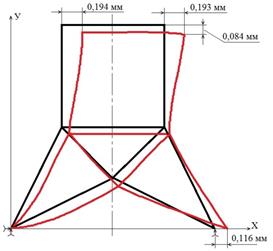
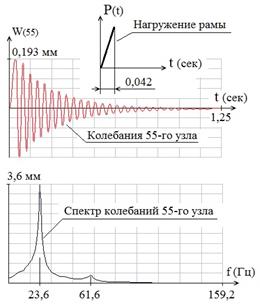
Мгновенное снятие нагрузки (динамический процесс)
Эпюра изгибающих моментов
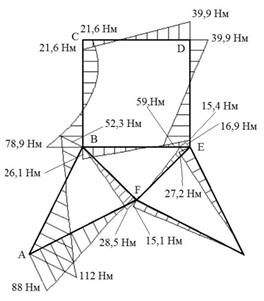
Рис. 3. Напряженно-деформированное состояние рамы при статическом нагружении и при мгновенном снятии нагрузки (динамический процесс)
По результатам динамического расчета на рис. 3 показаны горизонтальные перемещения 55-го узла в процессе свободных затухающих колебаний, из которых видно, что горизонтальное перемещение 55-го узла при статическом нагружении W55 = 0,193 мм совпадает с динамическим расчетом в момент снятия нагрузки, что говорит о правильности динамического расчета, т.к. до момента снятия нагрузки нагружение было медленным с точки зрения собственных частот рамы.
Приведенный на рис. 3 спектр горизонтальных колебаний 55-го узла рамы демонстрирует студентам, что доминирующей частотой в колебательном процессе рамы является частота собственных колебаний первого тона, другие собственные колебания быстро затухают, т.к. силы сопротивления пропорциональны скоростям.
Ценность конечно-элементного подхода в преподавании курса сопротивления материалов, строительной механики и теории колебаний инженерных сооружений состоит в следующем:
- осуществляется последовательная адаптация студентов к профессиональным КЭ-пакетам, применяемым на предприятиях;
- на экране студент в реальности видит деформацию объекта, что при традиционном изложении курса показать практически невозможно;
- сравнение конечно-элементных результатов с традиционными расчетами даёт студенту уверенность в правильности получаемых результатов и более глубокое понимание рассматриваемого явления;
- все строится на традиционных понятиях сопротивления материалов, строительной механики и теории колебаний.
Рецензенты:
Панов А.Ю., д.т.н., профессор, директор Института промышленных технологий машиностроения, заведующий кафедрой «Теоретическая и прикладная механика», Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Нижегородский государственный технический университет им. Р.Е. Алексеева», г. Нижний Новгород.
Грамузов Е.М., д.т.н., профессор кафедры «Кораблестроение и авиационная техника», Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Нижегородский государственный технический университет им. Р.Е. Алексеева», г. Нижний Новгород.
Библиографическая ссылка
Дербасов А.Н. ИНТЕГРИРОВАНИЕ КОНЕЧНО-ЭЛЕМЕНТНЫХ ПРЕДСТАВЛЕНИЙ В ДИСЦИПЛИНУ «СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ» // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18261 (дата обращения: 12.03.2026).



